劈尖干涉测细丝直径中测量点的选择
2014-02-02曲铁平李凤岐
曲铁平,李凤岐
(沈阳理工大学 理学院,辽宁 沈阳 110159)
利用劈尖干涉测定细丝直径作为等厚干涉的具体应用,是一项很好的设计性实验。由于此试验可以加深对等厚干涉理论的理解,培养综合能力,因而很多学者对此实验及其实际应用进行了系统研究[1-5]。劈尖干涉实验通常采用钠光灯为光源,条纹的清晰度随测量点不同会发生明显变化,影响测量精度,但对这一现象的解释还未见报导。本文用干涉条纹的反衬度对这一现象进行理论分析,指出测量点的合适位置,对劈尖干涉实验具有指导作用,并为研究钠光干涉提供参考。
1 实验原理及方法
空气劈尖用两块光学平板玻璃组成:将两块光学平板玻璃叠在一起,一端插入一细丝,在两玻璃板间形成空气劈尖。
待测细丝直径为[6]
式中:L为棱边到细丝处的总长度;Δn为记录的条纹数;l为Δn条干涉条纹对应的间距。
用钠光灯作为光源,通过JXD-250型读数显微镜观察干涉条纹,用数码相机拍摄不同级次的干涉条纹图像。
2 结果及讨论
干涉级次n分别为20、180及350各级干涉条纹的数码照片如图1所示。

图1 不同级次干涉条纹的数码照片
图1显示,不同级次干涉条纹的清晰度发生明显变化:级次n=20附近的条纹非常清晰,级次n=350附近的条纹非常模糊,而级次n=180附近的条纹的清晰度介于前二者之间。出现这一变化的根本原因是钠光灯所发光并非严格的单色光,而是包含波长非常接近的两条谱线,其波长分别为λ1=589.0nm和λ2=589.6nm。通过劈尖干涉形成的干涉条纹是这两个不同波长的谱线形成的干涉条纹的叠加,导致不同级次的条纹清晰度不同。
劈尖干涉光程差近似为[7]
式中,λ为入射光波长,d为干涉条纹所在处对应的劈尖厚度。当δ=(2k+1)λ/2 (k=0,1,2,…)时,形成第k级暗条纹,其对应的劈尖厚度为d=kλ/2。
由于钠光的两条谱线波长λ1≠λ2,因而二者的干涉条纹除特殊点(2d=k1λ1=k2λ2)外不重叠,导致干涉条纹的反衬度随劈尖厚度d而变化。
干涉条纹的反衬度[8]
式中:Imax为光强极大值;Imin为光强极小值;反衬度E反映的是干涉条纹的清晰度,其值介于0~1之间,E越大条纹越清晰。
劈尖干涉测量细丝直径实验中,劈尖厚度为d时,波长为λ1(与其对应的角频率为ω1)的谱线产生的两相干光的位相差为[7]
令劈尖上表面反射光为Asin(ω1t),则下表面反射光为Asin(ω1t+φ1),二者干涉后结果为
X1=Asin(ω1t)+Asin(ω1t+φ1)=2Asin(ω1t+φ1/2)cos(φ1/2)=A1sin(ω1t+φ1/2)
其振幅A1=2Acos(φ1/2)

同理,对波长为λ2的谱线有
为简化计算,上述推导中已假定两条谱线的反射光振幅皆为A(与实际情况基本相符)。
由于λ1≠λ2,两条谱线之间无干涉[7],总光强I应为二者各自干涉后光强的线性叠加。

不同级次干涉条纹反衬度的理论值如表1所示(取λ=589.3nm)。
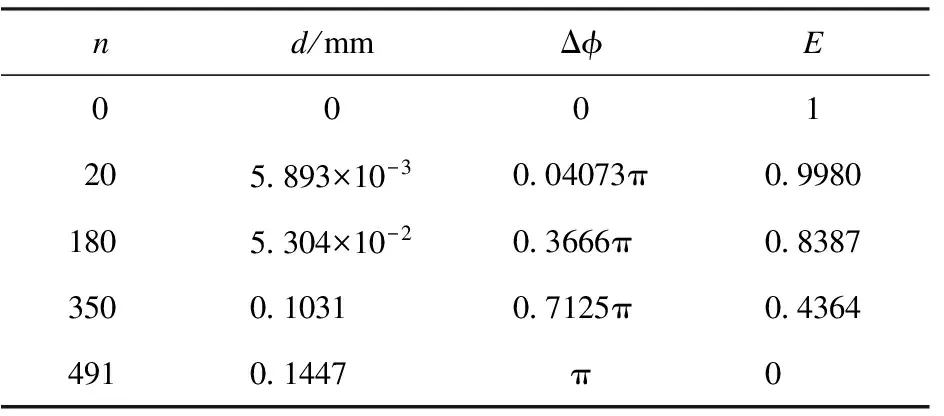
表1 不同级次干涉条纹的反衬度
从表1可以看出,当Δφ<π时,随级次n由0逐渐增加到491,相应的劈尖空气薄膜厚度d由0逐渐增加到0.1447mm;Δφ由0逐渐增加到π,干涉条纹的反衬度E则由1逐渐减小到0,且随着n的增加,E的减小速度越来越快。这是由于E随Δφ的变化率为
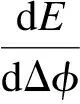
由于当级次n由0逐渐增加到491时,反衬度E由1逐渐减小到0,对应的干涉条纹由清晰逐渐变为完全消失,所以测量点应选在劈尖棱边一端。
3 结论
利用劈尖测量细丝直径时,劈尖棱边干涉条纹级次较低的位置反衬度约为1,条纹最清晰;当干涉级次增加到350(对应空气薄膜厚度为0.1031mm)时,反衬度已减小到0.4364,条纹变得非常模糊。因而测量点应选在棱边附近(级次n<100),避免选在待测细丝附近。
[1] 张兰霞,解顺强,王冀霞,等.劈尖干涉实验的误差分析及改进[J].中国校外教育(基教版),2009,12:147-148.
[2] 刘金龙.劈尖干涉条纹定域的解析研究[J].物理与工程,2008,18(4):54-57.
[3] 张国林,唐军杰,邵长金,等.劈尖干涉条纹变形原因的研究[J].大学物理实验,2003,16(2):14-16.
[4] 冯颖,宋瑞丽,王连加.利用劈尖干涉测定细丝直径的实验研究[J].东北电力学院学报,2003,23(2):46-49.
[5] 花世群, 骆英, 洪云.基于等厚干涉原理的液体折射率测量方法[J].中国激光,2006,33(11):1542-1546.
[6] 李志超.大学物理实验 [M].北京:高等教育出版杜,2001.
[7] 母国光,战之令.光学 [M].北京:人民教育出版社,1979.
[8] 吴强,郭光灿.光学[M].合肥:中国科学技术大学出版社,2003.
