风电系统风速预测算法的马尔科夫理论修正模型
2014-02-02宋建辉
于 洋,伊 跃,虞 闯,宋建辉
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159 )
随着社会的发展,煤炭、石油等地下资源正面临着枯竭的危险。而风能由于其储量巨大、清洁无污染和可再生的特点,具有广阔的发展前景。由于风能具有很强的随机性,当风电穿透功率超过一定值以后会严重影响电能质量和电力系统的安全性[1]。因此风速值的准确预测不但可以保证风能的利用率,而且还可以决定风力发电机的不同运行状态,确保风力发电机的并网操作和风电机组控制。
目前常用的短期风速预测方法有持续法预测、灰色系统理论、时间序列法、卡尔曼滤波法、小波分析及支持向量机算法等等[2]。以上方法有各自的优势,但又存在一定的局限性。如灰色系统理论对非平稳风速数据的预测不适用,神经网络需要大量的样本数据进行训练以及选取相近局域点困难等。众多算法之中,时间序列模型只需有限的样本序列即可建立精确的预测模型,因此该模型得到了广泛的应用。针对时间序列算法本身的适应性和预测精度等问题,不同学者提出了一系列的由多种预测算法组合建模算法。如文献[3]提出了利用小波分析法和滚动式时间序列法混合建模的短期预测优化算法,该算法实现了高精度的多步超前风速预测,但在多个风速预测点上面仍有较大的误差。文献[4]同样使用小波函数对非平稳风速信号进行多尺度分析与重构,利用重构后的低频平缓信号进行ARMA模型验证,该预测模型取得了一定的成功。但由于其只关注了低频平缓信号的主导作用,忽略了高频信号能量,因此模型的精确度不是很高。针对以上两种算法,本文提出利用马尔科夫理论修正的短期风速预测法。该方法利用小波分解与重构方法获取多层平稳风速信号,分层构建短期风速预测模型,以转移概率为标准选取合理的风速值,替换风速剧烈变化时的预测失真数据,并最终得到风速预测值。
1 基于马尔科夫理论的改进风速预测算法原理
基于马尔科夫理论的改进风速预测算法流程如图1所示。

图1 优化算法建模流程图
算法的实现主要包括以下4个计算过程:
首先,选择某小波基对拟预测风速序列进行n层分解与重构,以保证风速信号转变为多层的平稳风速序列。对分解后所得到的n层高频vi(t)(i=1,2,…,n)和1层低频风速序列ω(t)进行小波重构,获取相同尺度的分层风速信号。
其次,对n层高频和1层低频信号分别进行时间序列建模预测,计算得到各分解层的预测值。
再次,对各个分解层的预测值进行加权叠加,得到初步风速预测值。
最后,针对风速的强随机性,本文提出针对初步预测值利用马尔科夫转移矩阵进行修正,根据其状态空间的合理性进行风速数据的取舍以避免风速剧烈变化时的预测失真。
1.1 小波分解与重构
对于可在小波函数分辨率空间v(j)表示的某信号x(t),其可以利用分辨率空间v(j+1)和ω(j+1)空间中的基函数进行表示。即

(1)
式中:Al(k)反映了信号的低通成分,为信号的离散近似;Dl(k)为信号的高频成分,为信号的离散细节。小波重构为小波分解的逆向推导,将分解后得到的n+1组信号分别单独使用Mallat算法重构到原尺度,即可得到重构后的时间序列。
小波分解和重构,其信号的采样时间间隔越短,其分解程度越高,分辨率越好。但过高的分解尺度往往会造成过度分解[5]。综合多次试验数据,本文选择对风速数据进行层分解。
1.2 时间序列预测模型
本算法采用ARMA模型进行风速预测,其模型为
(2)
式中:φj、θj分别为待定的参数;x(t)表示为风速序列;ε(t)为正太高斯白噪声序列;p、q为模型的自回归阶数和移动平均阶数。
算法同时使用AIC准则函数来确定模型的阶数,AIC准则函数的定义为
(3)
当AIC(p,q)到达最小的时候,此时的p、q为最佳的模型阶数。
1.3 马尔科夫状态转移
国内外针对利用马尔科夫理论进行风速建模的应用已经进行了很多的研究,例如Sahin等[6]利用一阶马尔科夫模型进行土耳其的逐时风速序列建模,其最终证明90%预测结果符合客观风速的有效性。Kantz等[7]以风速为研究对象,将风看做是随机变量的时间序列,对风速建模并取得了较好的效果。以上研究表明马尔科夫链具有追踪变量随机波动的能力,同时马氏链具有无后效性。因此,利用马尔科夫模型与上述两种模型进行有机结合,可以有效提高模型的预报精度,避免风速信号随机波动较强时预测模型所产生的误差。
马尔科夫链的基本特征为:随机实验,每一实验只有有穷个或可列的无穷多个基本事件E(i)(i=1,2,…,N)可能发生,对于任意时刻,如果状态E(i+k)对于过去状态的条件概率分布仅仅是状态E(i)的一个函数,即
P(X(i+k)=E(i+k)|X(1)=E(1),X(2)=E(2),…,X(i)=E(i))=P(X(i+k)=E(i+k)|X(i)=E(i))
(4)
式中X(i+k)=E(i+k)表示i+k时刻过程处于E(i+k)状态。满足以上恒等式的过程可以看做马尔科夫过程。令k=1,即可构建状态空间的一阶马尔科夫链。本算法根据风速数据的一阶马尔科夫链进行风速下一步状态判断与修正,以削减风速信号的强随机性。
传统的马尔科夫预测模型采取一阶马尔科夫链时其数据来源固定不变,由马尔科夫性质可知新时刻状态与很久前的数据关联不大。因此本算法采用滑动的一阶马尔科夫链,即当新数据到达后,替换掉部分历史状态值以得到新的一阶马尔科夫链[8]。
2 实例仿真
仿真的硬件坏境为:CPU:intel Pentium dual、内存1G、硬盘250G。仿真的软件环境为Windows XP操作系统,仿真软件为Matlab R2010B。
仿真条件:选取某风场的近一个月数据(共161条数据)作为历史数据,假定该数据能真实反映该地区真实风速,该地区的风速随机性与时间特性。横坐标为风速数据对应的时间点,纵坐标代表风速值。选取前130点作为训练,预测随后的15点数据。
仿真系统采用多个小波基进行风速信号的分解重构与预测,在实例分析中以选取DB4小波基的分解重构信号进行分析。在ARMA建模分析中以第3层低频分量a3(t)序列说明本文的ARMA算法步骤,其余各层序列的ARMA模型建立类似进行。
(1)选取DB4小波对原始风速序列进行分解,选取分解层数为3,利算Mallat算法对分解后的各层序列进行重构。其分解后的信号图与重构后的信号图分别如图2和图3所示。

图2 风速信号分解后的多层分量图
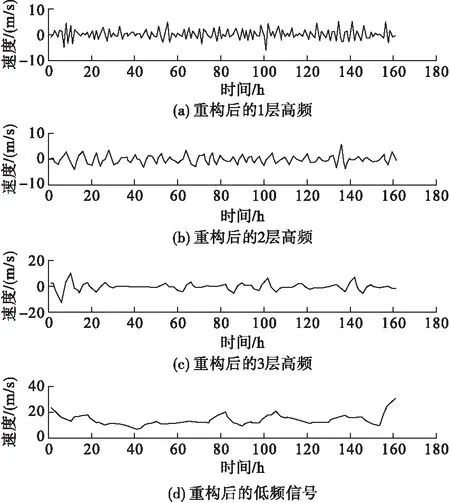
图3 多层信号重构后的分量图
(2)以a3(t)为例,建立ARMA模型,利用AIC准则进行定阶,选择最小二乘估计法估计参数。计算可得到合适模型:
x(t)-0.8933x(t-1)-0.7185x(t-2)+0.6128x(t-3)=ε(t)+0.792ε(t-1)-0.2571ε(t-2)-0.02404ε(t-3)-0.04197ε(t-4)-0.04547ε(t-5)+0.1076ε(t-6)+0.06922ε(t-7)-0.9112ε(t-8)-0.6932ε(t-9)+0.2015ε(t-10)
计量器具是用来评定机械产品是否合格的标准计量器具,判定产品是否合格,首先应保证计量器具的测量准确性,学生在测量过程中必须有维护、保养计量器具的态度,教师在讲解演示测量时,着重强调操作计量器具的注意事项,这是学生能否用好仪器的关键,要求每组有对应固定的测量器具,不能相互调换。责任到人,按规程操作,提高学生的责任意识,使仪器在使用中处于受控状态。实验结束后,要求学生把实验台收拾整齐,测量用具归回初始位置,摆放整齐被测件及仪器,教师检查合格后方可离开。
(5)
(3)利用上述步骤进行数据预测,得到包含低频信号特征的预测值x1(t)。预测结果和实际结果对比如图4所示,可以观测到利用一层平缓信号进行预测所得预测值与真实值有较大差距。

图4 低频信号预测图
(4)各层数据分别建立ARMA模型并进行数据预测,各层预测值进行加权叠加。本文选取加权系数为1。即
…
(6)
…

(5)利用小波函数与时间模型可有效预测风速,但针对风速强随机性存在一定的预测误差。因此本文采用马尔科夫算法进行算法修正。选取该风电场同季节的风速数据建立马尔科夫转移概率矩阵。历史样本数据容量为1540条,以0.3m/s风速作为状态空间的划分界限,构建风电场该季节的风速转移概率矩阵P。
(7)
式中转移概率pij定义为由状态空间E(i)经一步转移至状态空间E(j)的概率,计算公式为
(8)
算法以最近时间点的风速v(i)所处在的状态空间E(i)作为初始状态,利用矩阵P判断其下个时间点的风速值v(i+1)所处的状态空间E(j)是否合理。若pij存在一定的合理性,则说明当前状态有效并保留当前数据。若该概率小于0.05,则寻求距离E(j)最近的可能状态空间进行替换修正。
以本文算法为示例,在135点处,风速出现剧烈变化,由上一时刻的3.2m/s变化成为15.25m/s,利用小波函数与时间模型预测值为16.67m/s,与真实值具有较大差距。本算法将首先利用小波函数与时间模型预测获取初步预测值,马尔科夫修正过程中算法将首先寻找风速3.2m/s所处的状态空间E(10)经过一步转移后可达到的状态空间。E(10)经过一步转移后到达16.67m/s所在状态空间E(55)的概率为0,此时算法将进行马尔科夫修正,遍历寻找距离E(55)最近且转移概率大于0.05的状态空间,利用该状态空间的风速值进行修正。本例中,算法可寻找到状态空间E(52),即风速范围15.6~15.9m/s。更新预测值为15.75m/s。小波函数与时间模型预测方法和本文提出的马尔科夫修正算法预测结果如图5所示。
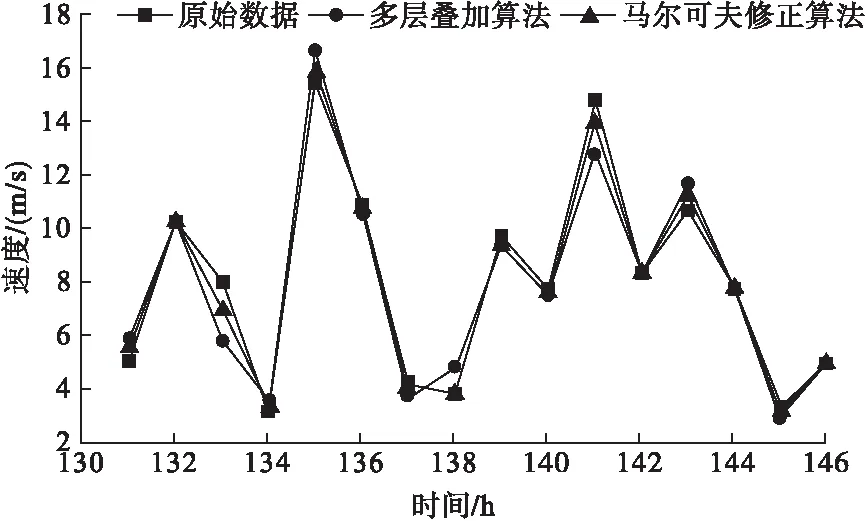
图5 两种方法风速预测值与真实值曲线图
利用图5对比可以很清晰的得到,风速预测值经马尔科夫修正后进一步提高了模型的精度,有效地减小了风速剧烈变化处的误差。
3 多种算法比较与误差验证
为验证本文模型的预测精度,采用平均误差、平方绝对误差、均方根误差、预测精度作为评价标准,其定义分别如下公式所示。
绝对误差定义为

(9)
平均误差定义为
(10)
平方绝对误差定义为
(11)
均方根误差定义为
(12)
精度定义为
(13)
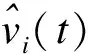
多种算法预测结果的误差以及精度分析如表1所示,其中算法一表示使用低频平缓信号的预测算法;算法二表示使用多层信号叠加的预测算法;算法三为基于马尔科夫理论的改进风速预测算法。
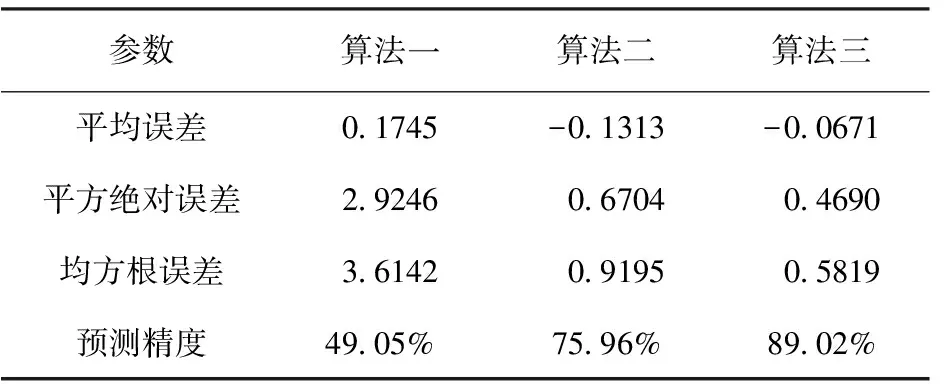
表1 多种预测算法预测结果对比
通过分析表1可知:基于马尔科夫理论的改进风速预测算法所建模型的各项预测评价指标值均优于传统的预测算法所对应的指标值。
本文采用多个小波基进行信号处理,不同的小波基其预测效果不尽相同,对此本文列举如表2所示的小波基预测误差。

表2 多个小波基分解重构后的误差值
从表1、表2可以看出,不同小波基的选择有着不同的预测结果,考虑到风速的高度随机性,风速信号小波分解后的各层分量应同时具有随机性信息,表现为类似脉冲信号的特性,因此选择DB4小波具有更好的预测精度。同时风速信号的准确预测应考虑多个学科领域,其历史数据的选取不应只是近一段时间的数据,而是应该选取一些与预测时间相关性较强的数据,如与当天的气候条件相似的历史数据,其预测精度将进一步提高。
4 结论
风速的准确预测对风电事业的发展具有重要的意义。利用小波分解重构算法和ARMA模型在短期风速预测中已有良好的预测精度,但仍存在一定的预测误差。本文提出的马尔科夫修正风速预测算法,很好地解决了风速预测时风速剧烈变化的失真问题。同时在没有增加数据处理工作量的基础上基本实现了风速准确快速预测。本文测试了多个小波基对风速预测的准确性,结果表明采用DB4小波基对风速信号进行分解与重构能够最准确地表发风速信号的变化特征。与多种传统预测方法相比较,本算法提高了风电场短期风速预测精度。
[1] 时庆华,高山.基于ARMA和卡尔曼滤波的风电场风电功率预测研究[C].长沙:中国高等学校电力系统及其自动化专业第二十五届学术年会,2009:72-76.
[2] 张华,曾杰.基于支持向量机的风速预测模型研究[J].太阳能学报,2010,31(7):928-932.
[3] Li Hui,Tian Hong-qi,Li Yan-fei.Short forecasting otimization algorithm for wind speed of windfarms based on wavelet analysis method and rolling time series method[J].Journal of central south university(science and technology),2010,41(1):370-374.
[4] 李玲玲,李俊豪,王大为,等.基于小波分析和时间序列的风速预测[J].陕西电力,2011,39(12):36-39.
[5] DU Wei-liao,ZHU Ru-mi,LI Yan-ming.Adaptive selection of optimal decomposition level in filtering algorithm based on wavelet transform[J].Journal of optoelectronics laser,2010,21(9):1408-1411.
[6] Sahin A D,Sen Z.First-order Markov chain approach to wind speed modeling[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89(3/4):263-269.
[7] Kantz H,Holstein D,Rgwitz M,et al.Markov chain model for turbulent wind speed data[J].Physica A:Statistical Mechanics and its Applications,2004,342(1/2):315-321.
[8] 赵琳琳,夏乐天.灰色马尔科夫链模型的改进及其应用[J].河海大学学报(自然科学版),2007,35(4):487-490.
