固体火箭多约束耗尽关机的动态逆能量管理方法①

张志健，王小虎

(北京控制与电子技术研究所，北京 100038)

0 引言

与液体火箭相比，固体火箭具有结构简单、安全性好、可靠性高、维护操作简便、准备时间短等特点，被广泛用于航空、航天领域。但固体火箭不具备关机能力，要获得满足特定飞行任务的能量，须采用耗尽关机制导技术，在关机之前，通过改变飞行姿态，消耗多余能量实现期望速度。该技术可降低或解除对复杂反向推力系统的依赖，减小结构质量、提高可靠性;可有效扩大载荷(空间卫星、弹头、滑翔飞行器)飞行范围，使固体火箭发动机能应用于更广泛的任务。近年来，随着快速空间响应、助推滑翔飞行器、高轨拦截等课题的兴起，固体火箭发动机能量管理制导作为一项关键技术，再次成为热点受到广泛关注［1－6］。

固体火箭大气层外耗尽关机制导技术包含两部分:一是根据目标和轨迹约束计算期望关机速度;二是根据发动机剩余能量、当前速度和期望速度进行耗尽关机能量管理。耗尽关机能量管理可分为两大类:一类能量管理基于零射程线［7－8］，其原理是将推力置于不影响射程的方向，从而对关机时间偏差不敏感，但该方法不具备多约束能力;另一类具有速度控制能力，该方法使飞行器在关机时达到指定速度矢量。本文研究速度可控的多约束耗尽关机能量管理。

速度可控能量管理可细分为开环和闭环:(1)开环方式，有姿态调制能量管理［9］，将能量管理飞行分为6段，在能量管理前完成各段姿态指令计算。因是开环策略，姿态调整次数多，易受干扰影响、精度差、且不利于大能耗管理，所以出现了一些减少分段的改进型［4，10］。(2)闭环方式，有通用能量管理和样条能量管理。通用能量管理［11］(GEM)简单而精确，但不能控制能量耗散强度，起止点攻角很大。为实现助推滑翔式飞行器助推末端水平速度、零攻角约束，徐衡、Liu Luhua 等提出了样条能量管理［1－2］(SEM)，可消耗较大能量，且具有末端约束能力。但其能量耗散强度不可控，导致大能耗管理时，在助推末段姿态角快速变化，不利于控制。

鉴于既有能量管理方式的不足，为了在不约束姿态角运动情况下简化能量管理问题，本文以多余视速度增量为状态变量，建立一种新型耗尽关机能量管理模型，并分析其特性;然后，根据关机约束，构建了一种闭环动态逆能量管理(IEM)方法，根据剩余飞行时间和多余视速度增量，规划多余视速度变化曲线，实现能量耗散强度可控的能量管理。

1 能量管理问题

多级火箭的上面级，已处于大气层外或大气密度很小，可忽略空气阻力。设飞行器初始速度为v0，发动机推力矢量F，关机时间tf，则能量管理目标是:在tf时，使速度矢量达到期望速度vr0:

其中，F大小不变、方向可控;g为重力加速度。飞行中，通过改变F的方向来达到目标。当固体火箭发动机装药量固定，发动机产生的总视速度增量S0为常值［12－13］，其大小为

式中 mf为关机质量;m0为起始质量;F为推力为质量变化率。

具有速度控制能力的耗尽关机能量管理，便基于S0为定值，通过规划飞行姿态消耗多余能量来实现。式(1)形式的速度控制，有3个自由度，不利于能量管理设计，故以往都将三维空间能量管理约束到二维平面内(俯仰平面、偏航平面或由待增速度和重力方向构成的平面)。该降维虽然可行，却约束了飞行器姿态运动范围，限制了能量管理方式的多样性;且当能量消耗大，须进行正、负两方向的快速姿态调转，不利于跟踪控制。

2 基于动态逆的能量管理方法

本章建立以多余视速度增量和趋近角为状态量的能量管理模型，不作平面约束，将三维问题降为二维;然后给出一种基于动态逆的能量管理策略。

2．1 多余能量为状态的数学建模分析

设期望在tf时刻达到速度vr0，因飞行器处于重力场，为补偿重力影响，构建虚拟期望速度vr:

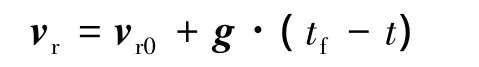
又设剩余视速度增量为S，当前速度v到vr矢端长度L，则瞬时多余视速度增量P为

若期望速度可实现，则必有P＞0。能量管理目的是寻找姿态角变化律，在关机时实现期望速度。

为简化问题，假设:(1)能量管理过程，发动机推力与飞行器纵轴重合;(2)期望速度的变化可忽略。飞行器姿态、速度、期望速度的位置关系如图1所示。图1中，α为攻角;γ为推力与OAB平面夹角;OAB平面指速度与期望速度所成平面。

图1 空间几何关系Fig．1 Space geometry relationship

因vr的虚拟重力场与v所受重力场相同，故L大小仅受推力影响。设趋近角∠ABO为θ，则:

整理可得

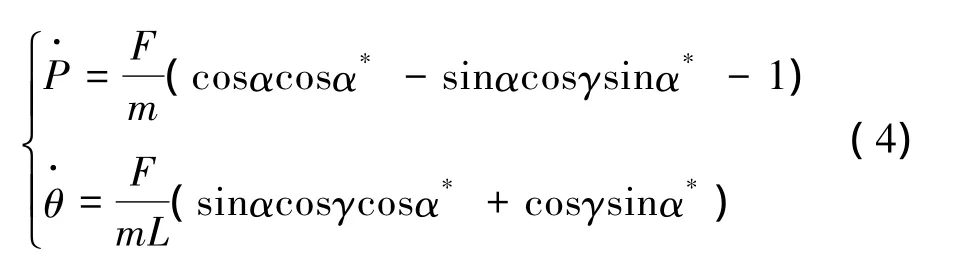
其中，m为当前质量;视加速度F/m可测;α*是速度与的夹角;L是 的长度，故:

式(4)即能量管理新模型，能量管理目的是设计姿态角α、γ的变化律，使关机时P=0。

基本性质1 式(1)形式能量管理，等价于:

该性质可由式(4)第一式得到。

该性质可由式(4)第二式得出，而要使γ有解，须满足α≥α*。

该性质表明，存在一条分界线，在该线一侧，趋近角变小，另一侧变大。

该式表明，即使保持趋近角不变，通过改变α亦能控制多余视速度增量的消耗。若关机时=0，必有α=α*=θ，且此时γ有唯一解γ=180°。所以，要减小关机攻角，须减小趋近角θ。

2．2 动态逆能量管理

其中

式中 u为输入量;X为状态量;δ为飞行姿态，δ有界，满足‖δ‖2≤1;B、A(t，v)、K(t，v)均为变参数矩阵，其中A为酉矩阵，满足AAT=I。

动态逆法关键是根据期望多余视速度消耗率，求解指令姿态α、γ，使如下泛函值最小:

其中，γ∈［0，180°］，若飞行中限制最大攻角为 αmax，则α∈［0，αmax)。

当α、γ存在实数解，则

由此可得 αc、γc。

设相关增益为kα、kγ，则控制指令可取为

2．2．1 期望多余视速度增量变化率

由于采用动态逆方法，只要设计合理的变化轨迹，便可实现耗尽关机能量管理。

［定理1］ 当不考虑姿态角限制和姿态变化的动态过程，则若期望多余视速度变化率为

且k＞1时，可在关机点实现需要速度。

证明:

即

故变化率关于时间的表达式为

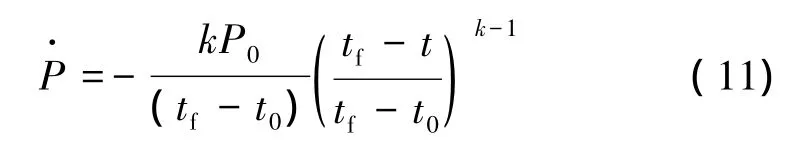
证毕。

k＞1意味着多余视速度增量的非线性消耗，且离关机越远、k越大，消耗的越快，(α，γ)能更快趋近(α*，180°)。

2．2．2 过程约束对P的影响

上节讨论能量管理的收敛性，实际飞行中，还要求指令信号变化平缓，以满足结构强度、控制能力、跟踪精度的需求。本节讨论姿态指令平滑性对P的变化律的影响。

从图1可见，若推力方向与OAB平面存在夹角，则飞行器速度矢量会绕虚拟期望速度旋转，旋转角速度为

式中 ωmax为旋转速度限制。

因速度相对期望速度的夹角和α、γ共同形成飞行器在惯性空间的姿态。该旋转速度直接影响飞行器的姿态变化，飞行中应限制旋速。

在能量管理关机时刻，有L→0，由式(12)可知，若sinαsinγ≠0，则ω→∞。速度矢量绕期望速度矢量快速旋转，导致俯仰、偏航姿态高频振荡。注意到P·→0，联系性质2和式(12)，要使关机时旋速趋近零，必有γ→180°，故要实现关机时姿态不振荡，应当有γ=180°。此时由式(4)第一式可得

其中，α－α*可代表飞行器体轴与AB线夹角。若令β=α－α*，则

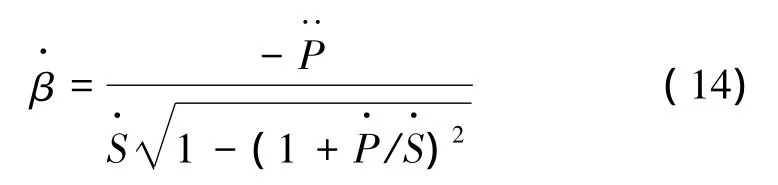
在制导中，应使β变化缓慢，即应满足:

［定理2］ 多余视速度增量按如下规律变化时，式(15)成立:

其中，k＞3。

证明:

由定理1可知，存在时间t0，当 t＞t0是可实现式(10)所对应的变化曲线。故当t＞t0有

代入式(14)右侧整理得

证毕。

定理2阐明:关机点附近，要使姿态角变化率很小，P应是时间的3阶以上曲线。而离关机较远时，可视P的大小调整系数k，减缓P的消耗速度，提高对期望速度变化的适应性。

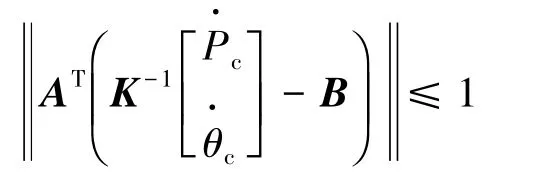
因A为酉矩阵，故

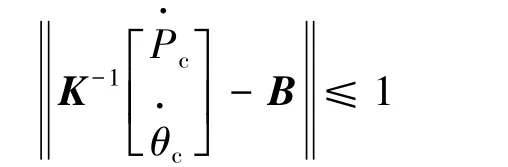
即

(1)平面内能量管理

采用该指令，平面OAB不旋转，是一种平面能量管理，与传统能量管理方法维度一致。该方法在能量管理过程中，∠ABO单调递增。

(2)螺旋能量管理

式(12)中，当 v、vr确定，旋转速度由 α、γ 决定，而α、γ由、确定。所以，旋转速度受约束时，应考虑与ω的关系。

当 和ω梯度方向一致时，等 线和等ω线条相切，切点满足:

由于旋速受限，能量管理中，会存在一条等ωmax线，α、γ的取值不能进入其所包含区域，据此可确定指令范围，本文给出一个求限定条件下αc、γc的方法，其步骤如下:

b．由(α0，γ0)确定该下最大旋速 ω0。

c．若 ω0≥ωmax，则取等 ωmax线和线交点对应的(α，γ)作能量管理指令。若 ω0＜ωmax，说明该线上所有组合都可作为能量管理指令。此时，为保证指令连续和α收敛，用如下方法确定指令(αc，γc)。

首先计算αc:

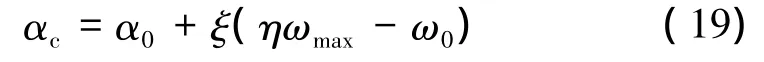
其中，0＜η＜1;当α受约束，则限制αc取值。

然后根据式(8)确定γc。由此实现使攻角逐渐变小的螺旋能量管理。

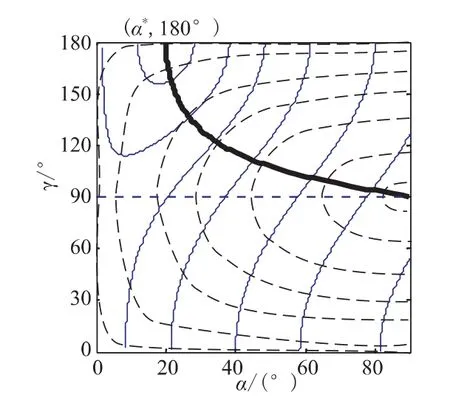
图2 等 线与等ω线的关系Fig．2 Isoline of and ω

当 ξ＞0 时，若 ηωmax＞ω0，则有 αc＞α0，从图 2 可知，在相同多余视速度消耗率下，对应的γc角更接近 ，速度矢量更快地向期望速度靠近;若ω0＞ηωmax，则相反:γc处于黑线下方，θ角增大，式(12)分母增大，使可实现的最大旋速ω0逐渐减小，直至小于ηωmax。该方法能在保证最大旋转速度不超限的情况下，更快地收敛到期望速度。另外，根据性质3，黑色粗线是趋近角θ变大、变小的边界线。所以，ξ正负直接影响关机时刻θ角的大小，从而决定关机攻角大小。其中，当ξ为正时，θ逐渐变小;为负时，θ变大，不利于实现末端零攻角，应避免采用。

3 仿真分析

本章通过数学仿真分析所提方法的特性和效果，分3部分:(1)重要参数影响;(2)不同期望速度的能量管理性能;(3)与已有方法进行对比。

仿真中假设平面地球，该多级飞行器数据参考文献［1］，第三级点火时:水平速度 3 453．4 m/s，垂直速度 569．4 m/s，秒耗量= － 32．639 kg/s，推力 F=95 110 N，初始质量 m0=2 401．3 kg，攻角为零，发动机工作时间t=50 s。发动机总视速度增量为3 316．8 m/s。飞行过程约束:姿态角速度小于10°/s。

3．1 多约束动态逆能量管理参数特性

3．1．1 参数 k 的影响

设关机期望速度为水平6 000 m/s。此时多余视速度增量占总视速度增量的23．2%。

应用平面能量管理时，飞行器只在纵向面内转动，可用俯仰角、俯仰角速度来描述姿态变化。k分别取2、3、5 时，能量管理结果见图 3。

图3 多余视速度增量、俯仰角、俯仰角速度变化曲线Fig．3 Curves of excess velocity capability，angle of pitch and pitch velocity vs time

由图3可见，k越大，P越快地接近0，前半段消耗越多;与之对应，在前半段:k越大俯仰角越大、大角速度持续的越长。这是因为相同多余视速度增量下，k越大越大，需用姿态角越接近最大耗能姿态。关机点附近，当k=3，俯仰角速度基本不变;当k=2，则越接近关机点，俯仰角速度越大;当k=5，越接近关机点，角速度越小。与定理2一致。

3．1．2 参数 ξ的影响

当采用螺旋方式管理能量，不管ξ取何值，其速度矢量都将在惯性空间螺旋。ξ不同螺旋轨迹不同。下面给出k固定，ξ变化时的仿真结果。其中，期望关机速度取水平6 000 m/s。

图4为速度矢量在沿虚拟期望速度方向的投影。可知，ξ越大，速度矢量越快地贴近期望速度。需要说明的是若ξ绝对值很小，则式(19)右侧第二式的调节能力非常小，飞行中旋速始终接近最大可达螺旋。此时，若速度矢量过早接近虚拟期望速度，则可能导致旋转速度过快，超出角速度限制。所以，ξ绝对值不应过小。从图5可知，相对于ξ=0，当ξ为负，则推力使速度矢量远离虚拟期望速度，关机攻角大;当ξ为正，则推力使速度矢量贴近虚拟期望速度，关机攻角小。另一方面，从图6可知，相对于负ξ，能量管理过程中，正ξ飞行的姿态变化速度会加快，这是速度矢量更快地贴近期望速度矢量的必然结果。

图4 速度在期望速度轴向的投影Fig．4 Velocity projection on vertical plane ofvr

图5 姿态角α和γ的轨迹Fig．5 Trajectory of α and γ

图6 飞行器的最大角速度Fig．6 The maximum angular velocity

3．1．3 大范围能量管理精度

IEM具有大范围能量管理特点，为统计不同强度能量管理特性，每隔100 m/s给出4 000～6 700 m/s水平关机速度管理结果，详见图7。此时多余视速度增量占总量的 2．1%～83．3%。

图7 不同期望速度的能量管理结果Fig．7 Energy management results of difference desired velocity

由图7可见，速度大小偏差在3．2 m/s以内，速度与期望速度的夹角在0．013°以内。关机偏航角小于20°，姿态角速度小于 1．5°/s，有利于关机后的飞行动作如姿态调转、级间分离等。尤其当能量耗散率小于41．3%(期望速度大于5 400 m/s)，速度大小偏差小于0．25 m/s，角速度小于 0．25°/s，关机攻角小于 5°，且关机速度越大攻角越小，说明该方法具有很高的速度控制精度。当能量耗散率大于44．3%(期望速度小于5 300 m/s)，随着速度减小攻角迅速增大，这是因为攻角小意味着推力基本用来增加速度;当能量耗散率大，则须进行长时间、大强度机动飞行。所以，耗散率增大，攻角会增大。需要说明的是本仿真中对不同的耗散强度，采用了相同的 k、ξ、η、kα、kγ。其中，η=0．7、ξ=0．07、k由零时刻2增加到关机时刻的3．3。说明该方法具有鲁棒性很强的特点。

3．2 3种不同的闭环能量管理方式

为研究本方法与其他具有速度控制能力的闭环能量管理方式的异同，与GEM、SEM方法进行了对比，结果如图8所示。期望水平速度6 000 m/s。

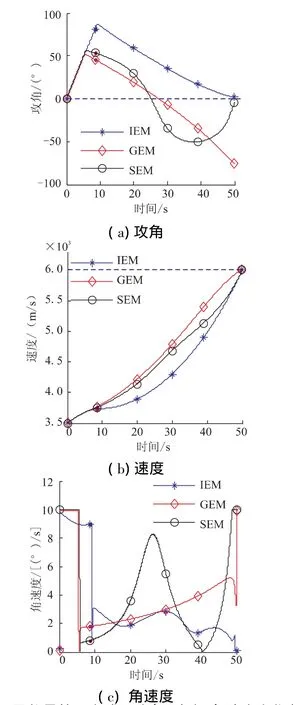
图8 不同能量管理方式下攻角、速度、角速度变化曲线Fig．8 Angle of attack，velocity，and angular velocity under different method

由图8可见，这3种方式都具有很高的速度控制精度。其中，由于GEM采用圆弧轨迹管理多余能量，不具备攻角约束能力，其末端攻角会非常大，达到78．2°，而 SEM 只有 3．9°，IEM 只有 2．6°，详见图 8(a)。正因为SEM、IEM末端攻角小，故关机点附近速度增加快;GEM攻角大，速度增加慢(图8(b))。在角速度方面(图8(c))，因SEM方法采用三阶多项式规划速度变化轨迹，所以姿态出现起始、中间、末端3次快速变化;而GEM虽然中间段姿态变化平缓，但末端姿态快速变化。相比之下，除起始时刻建立姿态的过程，IEM方式姿态角速度一直小于前2种方法;其角速度大小虽小幅起伏，但在整个过程中具有减小趋势，尤其在关机点附近角速度需求远小于前2种方式。因此，IEM方法的制导指令更有利于控制实现。

4 结论

(1)针对传统能量管理方法不利于多约束耗尽关机，定义了趋近角并结合多余视速度增量建立了新型能量管理模型，该模型与传统能量管理模型等价，可作为速度可控耗尽关机问题的一种新的数学描述。

(2)基于动态逆的能量管理方式设计简单，设计参数只有2个，且仿真结果表明参数设计具有非常强的鲁棒性。

(3)该方法能量管理具有精度高、能量管理范围大、角速度小、末端攻角小的特点，可满足关机点速度、攻角、角速度等多约束。

［1］ Heng X，Wanchun C．An energy management ascent guidance algorithm for solid rocket-powered launch［C］//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference．2011，Grand Hyatt，San Francisco，California．

［2］ Liu L，Chen K，Tang G．Research of multi-restriction energy management of solid rocket［C］//5th International Conference on Recent Advances in Space Technologies．2011，Istanbul，Türkiye．

［3］ 李新国，王晨曦，王文虎．基于修正Newton方法的固体火箭能量管理方法研究［J］．固体火箭技术，2013，36(1):1-5．

［4］ 姚党鼐，张力，王振国．姿态角单次调整的固体运载火箭耗尽关机能量管理方法［J］．国防科技大学学报，2013，35(1):39-42．

［5］ 陈峰，王育林，肖业伦，等．基于预测脱靶量的远程拦截速度增益导引［J］．航空学报，2008，30(06):1665-1672．

［6］ 胡正东，郭才发，曹渊，等．轨道轰炸飞行器过渡段轨道设计与制导［J］．固体火箭技术，2009，32(05):473-477．

［7］ White J E．Cut-off insensitive guidance with variable time of flight［R］．AIAA 93-3785．

［8］ 周军，潘彦鹏，呼卫军．固体火箭的鲁棒自适应耗尽关机制导方法研究［J］．航天控制，2013，31(3):34-39．

［9］ Patha J T，Mcgehee R K．Guidance，energy management，and control of a fixed-impulse solid-rocket vehicle during orbit transfer［R］．AIAA 76-1920．

［10］ 刘新建，袁天宝．固体小运载的制导方案设计与仿真［J］．系统仿真学报，2005，17(11):2734-2736．

［11］ Zarchan P．Tactical and strategic missile guidance［M］．New York:AIAA Inc，2007．

［12］ 陈世年，李连仲，王京武．控制系统设计［M］．北京:中国宇航出版社，1996．

［13］ Wiesenberg B．Improvements in reusable solid rocket motor performance predictions［R］．AIAA 2000-3182．