定时截尾情形下指数分布参数的估计

刘银萍，张雨嫡，秦 青

(吉林师范大学 数学学院,吉林 四平 136000)

近年来,关于截尾情形的统计推断问题引起了人们广泛的关注[1-5].指数分布是可靠性寿命试验中的基本分布之一.关于指数分布总体的统计推断问题,无论是完全数据还是缺失数据,一直都吸引着统计工作者对其进行研究[6-10].文献[6] 给出了部分缺失数据情形下指数分布总体的参数估计和检验;文献[7] 给出了指数分布总体在定时截尾和数据缺失场合下参数极大似然估计;文献[8]给出了定数截尾缺失数据场合指数分布参数Bayes估计.本文对于定时截尾情形指数总体的参数极大似然估计及其性质做了进一步的讨论,给出了指数总体参数的极大似然估计,证明了极大似然估计的强相合性质及渐近正态性质.

1 参数的极大似然估计

设指数总体X，其概率密度函数为

其中λ>0为未知参数.

对总体X进行n次独立的观测,直到时刻K0停止.设总体的样本观测量为Y1,Y2，…，Yn,其中Yi=Xi∧K0，这里a∧b=min(a,b),Xi为来自总体X的第i个样本的寿命,K0>0为给定的常数,称为阈值.则Y1,Y2，…，Yn独立同分布.且

当Xi0

当Xi≥K0时，Yi=K0概率函数为p(x)=P(Yi=K0)=P(Xi≥K0)=e-λK0

似然函数为

对数似然

令

解得λ的极大似然估计为

2 极大似然估计的渐近性质

证明由于Eδ1=P(Y1=K0)=P(X1≥K0)=e-λK0

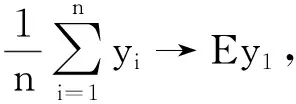
由Slutsky定理[11]，

引理记Sn=(S1n,S2n，…，Skn)T，β=(β1,β2，…，βk)T，设

证明令Wi=(δi,Yi)T

则{Wi,i=1,2,…，n}是独立同分布的随机变量序列

且

令

∑=E[(W1-EW1)(W1-EW1)T]

由多元中心极限定理可得

其中

又

则

令

则有

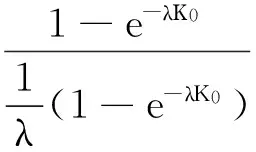
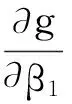
由引理知

其中

[1]SUN Xiao-qian,ZHOU Xian,WANG Jing-long.Confidence Intervals for the Scale Parameter of Exponential Distribution Based on Type Doubly Censored Samples[J].Journal of Statistical Planning and Inference,2008,138(7):2045～2058.

[2]徐晓玲，定数截尾缺失数据下 Weibull 分布的统计推断[J].数理统计与应用概率,1997，12(4)：363～370.

[3]韩 明.双参数指数分布无失效数据的参数估计[J].运筹与管理,1998，7(2):27～36.

[4]姜礼平.截尾正态分布的最小后验风险 Bayes 推断[J].应用概率统计与管理，2005，14(1):47～51.

[5]刘银萍,高 敏，王 艳.定时截尾情形具有部分缺失数据两个几何总体参数的估计和检验[J].吉林师范大学学报(自然科学版)，2013,34(3):10～14.

[6]刘银萍.具部分缺失数据两个指数总体的估计和检验[J].吉林大学学报(理学版), 2002,40(3):255～257.

[7]王乃生，王玲玲.定数截尾数据缺失场合下指数分布参数的 Bayes 估计[J].应用概率统计,2002，17(3)：229～235.

[8]刘 函.定数截尾数据缺失场合下双参数指数分布参数的 Bayes 估计[J].武汉大学学报，2006，52(3):286～290.

[9]翟伟丽,茆诗松.定时截尾场合下双参数指数分布的参数估计[J].应用概率统计, 2002, 18(2): 197～204.

[10]田 霆,刘次华.定时截尾缺失数据下指数分布的参数AMLE [J].华侨大学学报:自然科学版, 2006, 27(4): 351～353.

[11]茆诗松,王静龙,濮小龙.高等数理统计学[M].北京:高等教育出版社, 2000.