应用哈密顿原理推导拉格朗日陀螺的运动微分方程

杨远贵，陈 三

(淮北师范大学 物理与电子信息学院，安徽 淮北 235000)

0 引言

哈密顿原理在分析力学中占有重要地位，特别是在工程技术方面得到广泛应用．由于哈密顿变分原理是在基本定律基础上采用变分法推得，其主要特征是将真实运动与在同样条件下的可能运动区分出来的准则，该原理作为有限元法和其他近似计算方法的理论基础，因此它已成为理论物理中重要的研究工具之一．哈密顿正则变换是以广义坐标和广义动量为变量而建立的系统的运动方程．由于正则方程结构简单、对称，为动力学的变换理论创造了有利条件，为正则方程渐进解法奠定了理论基础[1-2]．如哈密顿动力学系统的辛算法应用于多体的稳定性研究中[3]，最近有人提出基于哈密顿动力学系统新变分原理的保辛算法[4]．下面以拉格朗日陀螺为例来说明哈密顿原理在经典力学中的应用．

拉格朗日陀螺是各种现代化陀螺的原始雏形，建立和研究它的动力学模型具有重要意义．陀螺的主要特征是它的稳定性和进动性，已被广泛应用于航空航天、航海与自动化和现代化的国民经济建设中．我国在轨运行的天宫一号航天器就是采用的控制力矩陀螺系统进行导航[5]．拉格朗日陀螺是轴对称的重刚体(又称为对称陀螺，即I1=I2≠I3)，其重心位于动力对称轴上但不与固定点重合，它的运动微分方程的建立可以采用欧勒动力学方程和保守力系的拉格朗日方程[6-7]．下面采用哈密顿变分原理和正则变换推导拉格朗日陀螺的运动微分方程．

1 拉格朗日函数和哈密顿函数

图1是采用三个欧拉角θ，φ，ψ作为广义坐标来描述拉格朗日陀螺．在坐标系O-ζηζ中，自转轴OZ与Oζ之间的夹角为θ．重心G到坐标原点O的距离为l．

1.1 陀螺的拉格朗日函数

若选取O-ζη为零势能面，则拉格朗日陀螺的势能为：V=mglcosθ．

根据欧勒运动学方程:

(1)

考虑到对称陀螺的轴转动惯量I1=I2，可以得到拉格朗日陀螺的动能为：

因此，对称陀螺的拉格朗日函数为：

图1 拉格朗日陀螺

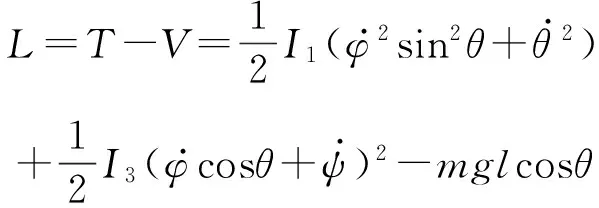
(2)

1.2 陀螺的哈密顿函数

由(2)式可以得到广义动量为：

(3)

根据哈密顿函数的定义，有：

(4)

2 推导拉格朗日陀螺的运动微分方程

拉格朗日陀螺的运动方程采用欧勒动力学方法较为复杂，而保守力系的拉格朗日方程较为简便，但它们都是二阶常微分方程．下面采用哈密顿变分法和正则变换方法来推导其运动微分方程．

2.1 哈密顿变分法

(5)

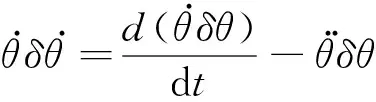
对上式积分可以得到：

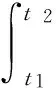
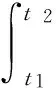
考虑等时积分，即有：δθ|t1=δθ|t2=0；δφ|t1+δφ|t2=0；δψ|t1=δψ|t2=0．又因为积分号内的δθ，δφ及δψ是任意的且一般不为零，且是相互独立的．因此有：

(6-1)

(6-2)

(6-3)

最后对(6-1)～(6-3)式的三个式子进行积分并化简，得到拉格朗日陀螺的运动微分方程为：

(7-1)

(7-2)

(7-3)

其中E、J和c为积分常数．

2.2 哈密顿正则变换法

首先根据哈密顿正则方程，计算拉格朗日陀螺的三个广义速度．

(8-1)

(8-2)

(8-3)

其次，计算三个广义动量．

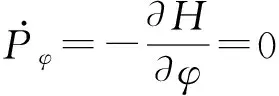
正则变换的最后一个广义动量：

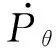
这就是(6-1)式，同样的办法积分即可以得到(7-1)式．

3 讨论

通过前面的推导可以看出，采用哈密顿变分法推导拉格朗日陀螺的运动微分方程的计算过程较为麻烦，而利用正则变换计算简洁，考虑循环坐标直接可以得到一阶运动微分方程．这样使得复杂的问题得到大大简化．

[1]黄昭度，纪辉玉.分析力学[M].北京：清华大学出版社，1985.

[2]Hand L.N.,Finch J.D.Analytical mechanics[M].Cambridge:CUP,1998.

[3]Chambers J.E.A hybrid symplectic integrator that permits close encounters between massive bodies[J].Mon.Not.R.Astron.Soc.,1999，304(4)：793～799.

[4]高 强,彭海军,张洪武,等．基于哈密顿动力系统新变分原理的保辛算法之一：变分原理和算法构造[J].计算力学学报，2013，30(4)：461～467.

[5]张锦江,范松涛,张志方,等．天宫一号基于控制力矩陀螺的智能多模自适应姿态控制系统设计与验证[J].中国科学：科学技术，2014，44(2)：131～141.

[6]周衍柏.理论力学教程[M].北京：高等教育出版社，1986.

[7]丘名实.应用拉格朗日方程建立重力作用下轴对称刚体的运动微分方程[J].海南大学学报(自然科学版)，2000,18(1)：105～108.

[8]胡中为，萧耐园．天文学教程(上册)[M].北京：高等教育出版社，2003.

[9]夏一飞，黄天衣.球面天文学[M].南京：南京大学出版社，1995.

[10]董连政，王金平．高师理论力学教学的创新与实践[J]．吉林师范大学学报(自然科学版)，2006,27(1)：82～83.

[11]朱光平，刘忠良，刘亲壮.量子力学态叠加原理及教学的几点看法[J]．吉林师范大学学报(自然科学版)，2010,31(3)：108～110.

[12]廖耀发，佘守宪.陀螺与陀螺仪进动及章动的一种初等分析[J].湖北工学院学报，2004,19(5)：43～46.