多参数优化方法减小永磁电机齿槽转矩

王 慧，王艾萌，王春梅

(华北电力大学，保定071003)

0 引 言

永磁电机具有结构简单、体积小、重量轻和高效节能等优点［1］。永磁电机中的齿槽转矩来源于开槽电枢铁心与永磁体的相互作用，齿槽转矩导致电机转矩脉动，引起噪声和振动，减低系统的控制性能。

国内外学者对如何削弱齿槽转矩、减小转矩脉动做了很多研究，文献［2－8］提到多种减小齿槽转矩的方法，其中就包括转子斜极。实现转子斜极的方法主要有两种，一种是转子磁极整体倾斜，即连续斜极;另一种是转子磁极在轴向上分成几段，并沿圆周方向错开一定的角度，即分段斜极。

极弧系数对永磁电机齿槽转矩也有很大的影响，极弧系数的改变对齿槽转矩的幅值和波形都有很大的影响。对某一电机来说，它存在最优极弧系数，偏离这个值时，齿槽转矩就会增大［9］。而采用单一方法，齿槽转矩的减小幅度有限，总会剩余齿槽转矩的一些谐波分量。

针对单一方法的不足，本文对转子分段斜极与优化极弧系数相结合减小齿槽转矩的方法进行了分析研究。针对一台电机磁极分段数分别为2 和3时，用有限元法进行仿真分析来说明分段斜极和优化极弧系数对齿槽转矩和反电势的影响。最后，通过试验结果与有限元结果的对比分析，验证了这两种方法结合削弱齿槽转矩的有效性。

1 分段斜极电机的齿槽转矩和斜极角

转子斜极是一种有效减小齿槽转矩的方法，其原理与定子斜槽类似，然而，与连续斜极相比，分段斜极工艺相对简单［2－8］，不仅能较好地减小齿槽谐波，还能降低加工成本。因此，本文用转子分段斜极进行分析研究。即将原来整个磁极用几段沿轴线方向长度相等的磁极来代替，并将各段沿圆周方向错开一定的角度排列［10］。图1 是轴向分段数为2 的电机转子，其中各段的轴向长度是相同的。

分段斜极电机的齿槽转矩表达式:

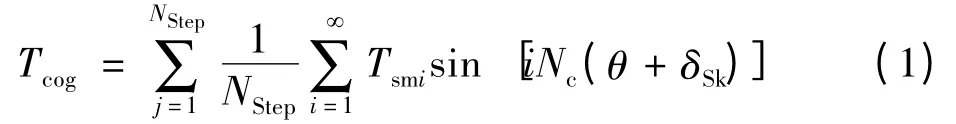
式中:Tsmi是没有分段斜极的齿槽转矩幅值;δSk是由式(2)得到的最佳斜极角;Nc是定子槽数和转子极数的最小公倍数;θ 是磁极与定子齿的相对位置角。

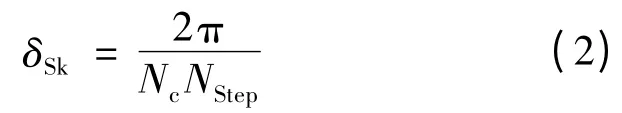
式中:NStep是轴向磁极分段数。

2 不同分段数的有限元分析

本文以18 槽6 极电机为例，分别对磁极分段数为2 和3 进行有限元分析。

2.1 磁极分段数为2

图1 是其电机转子示意图，轴向分段数为2，极弧系数αp=1，δSk=10°。图2(a)和图2(b)分别表示的是斜极角变化时齿槽转矩波形和齿槽转矩谐波，可以看出，偏移后齿槽转矩谐波仍然存在。虽然当斜极角δ 为最佳斜极角10°时，削弱了齿槽转矩基波分量，但偶次谐波，特别是二次谐波仍然存在。图2(c)比较了斜极角为0°和10°时的反电势波形。

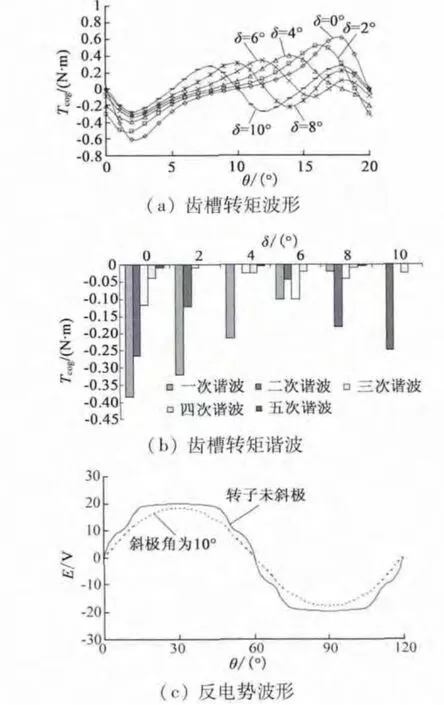
图2 αp =1.0 且分段数为2 时的齿槽转矩和反电势波形

下面采用最佳极弧系数与斜极相结合的方法来进一步减小齿槽转矩。由图2(b)可知，分段斜极能消除齿槽转矩的基波分量，可以进一步对极弧系数进行优化，以消除齿槽转矩的二次谐波分量。18 槽6 极的电机在不同极弧系数下的齿槽转矩波形和齿槽转矩谐波分别如图3 和图4 所示。由图4(b)可知，当极弧系数αp为0.90 或0.725 时，齿槽转矩的二次谐波分量几乎为零。

图4 电机没有斜极时不同极弧系数下的齿槽转矩谐波

图5(a)所示的是采用最佳极弧系数与分段斜极相结合的方法时齿槽转矩峰值的变化，即齿槽转矩峰值随极弧系数αp和斜极角δ 的变化。图5(b)表示斜极角为10°时，不同极弧系数下的齿槽转矩幅值，这证实了当极弧系数为0.90 或0.725 时，所得到的齿槽转矩最小。

图6(a)和图6(b)表示当αp= 0.9 时，电机不同的斜极角对齿槽转矩波形和谐波分量的影响。可以看出，斜极角为10°时，由于基波和二次谐波可以忽略不计，齿槽转矩明显地降低。

图6 分段数为2，αp =0.9，斜极角变化时的齿槽转矩

2.2 磁极分段数为3

对相同的18 槽6 极电机，分段数为3 时进行分析，如图7(a)所示，其中αp=1.0，δSk=6.66°。图7(b)、图7(c)为齿槽转矩波形和齿槽转矩谐波，而图7(d)表示的是斜极角分别为0 和6.66°时的反电动势波形，由图7(c)可知，利用最佳斜极角可以消齿槽转矩的基波和二次谐波分量。

虽然最佳斜极角为6.66°，可以消除基波和二次谐波的齿槽转矩分量，然而，其它奇次谐波，特别是三次谐波仍然存在。下面通过优化极弧系数进一步消除三次谐波分量，由图4(c)可知，当极弧系数αp=0.935，0.8275，0.725 或0.6 时可使三次谐波分量最小。

图8(a)表示的是当极弧系数和斜极角变化时，齿槽转矩峰值的变化;而图8(b)表示的是当斜极角为6.66°时，极弧系数变化时的齿槽转矩峰值。这验证了当极弧系数αp=0.935，0.8275，0.725 或0.6 时，可得到齿槽转矩的最小值。

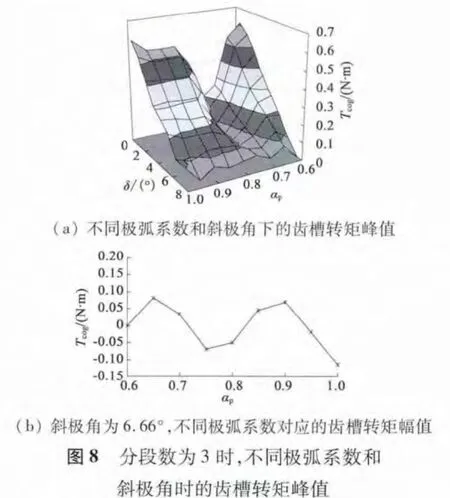
图9 表示当αp=0.8275 时的齿槽转矩波形和谐波含量。可以看出，当斜极角为6.66°时，因为齿槽转矩的基波，二次谐波和三次谐波分量可以忽略不计，齿槽转矩显著减少。图9(c)表示斜极角分别为0 和6.66°时得到的反电动势波形。

3 样机试验

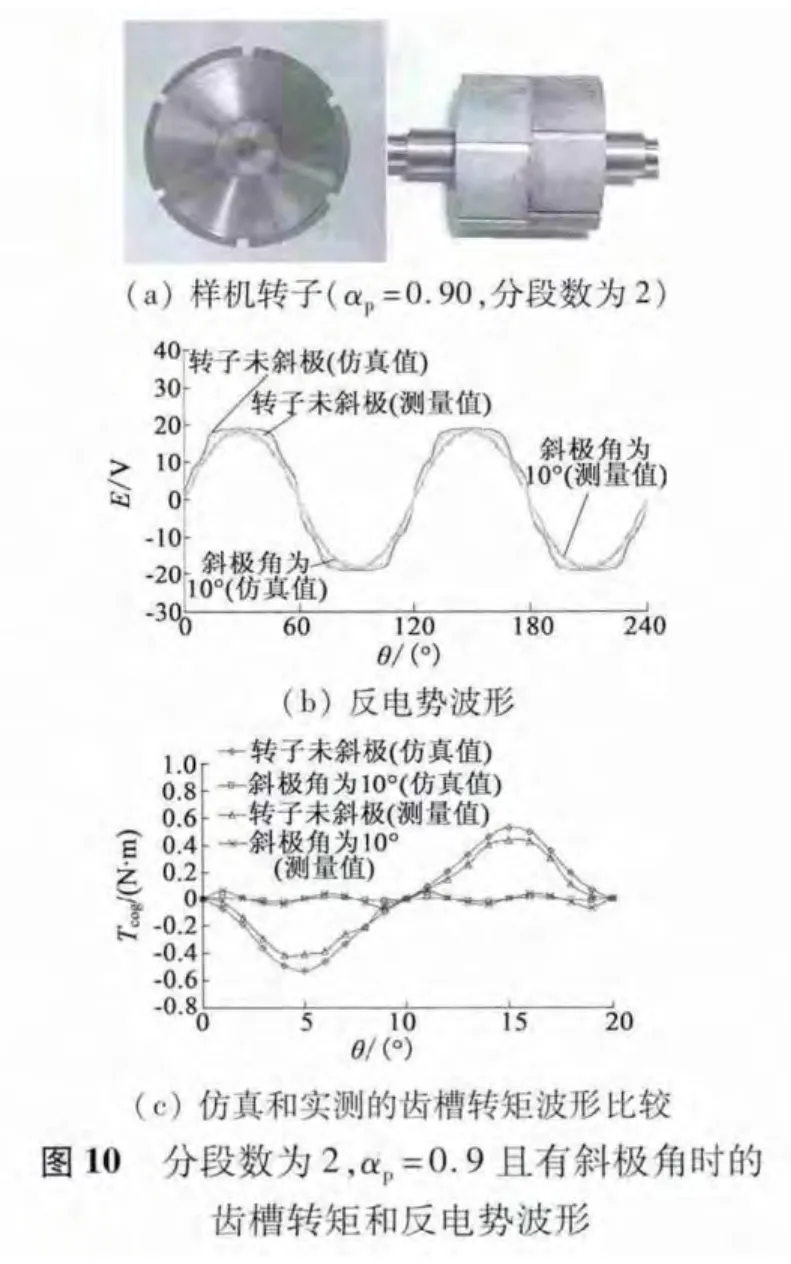
为了验证上述分析的正确性，对αp= 0.90，分段数为2 的样机进行了试验验证。图10(a)为样机的转子部分，此样机的斜极角为10°。图10(b)、图10(c)对比了试验实测与有限元仿真的反电势和齿槽转矩波形，两者结果基本吻合，验证了转子分段斜极和优化极弧系数减小齿槽转矩的有效性。

4 结 语

本文首先采用转子分段斜极法减小齿槽转矩，有限元结果表明此方法能有效减小齿槽转矩，但削弱幅度有限;优化极弧系数后，齿槽转矩可大幅度减小。通过合理确定磁极分段数和极弧系数，可以很大幅度地减小永磁电机的齿槽转矩。有限元分析结果和样机试验结果验证了此方法的有效性，该方法对削弱永磁电机齿槽转矩有一定的指导作用。

［1］ 唐任远. 现代永磁电机理论与设计［M］.北京:机械工业出版社，1997.

［2］ CALSON R，TAVARES A A，BASTOR J P，et al.Torque aipple attenuation in permanent magnet synchronous motors［C］//1989 IAS Annual Meeting.IEEE，1989:57－62.

［3］ KIM K H，SIM D J，WON J S.Analysis of skew effects on cogging torque and BEMF for BLDCM［C］//1991 IAS Annual Meeting.IEEE，1991:191－197.

［4］ WANG J P，LIEU D. A fast lumped parameter model for magnet skew in a motor［C］//IEEE Trans. on Magnetics，1999，35(5):3709－3711.

［5］ JAHNS T M，SOONG W L. Pulsating torque minimization techniques for permanent magnet AC motor drives－a review［J］.IEEE Trans. on Industrial Power Electronics Applicance，1996，43(2):321－330.

［6］ HANSELMAN D C. Effect of skew，pole count and slot count on brushless motor radial force，cogging torque and back EMF［J］.IEE Proc.of Electric Power Applications，1997，144(5):325－330.

［7］ KIKUCHI T，KENJO K. In－depth learning of cogging/detenting torque through experiments and simulations［J］. IEEE Trans. on Education，1998，4(4):352－352.

［8］ BINNS K，CHAABAN F，HAMEED A.Major design parameters of a solid canned permanent magnet motor with skew magnet［J］.IEE Proceedings B Electric Power Application，1993，140(3):161－165.

［9］ DEODHAR R P，STATION D A，JAHNS T M，et al. Prediction of cogging torque using the flux－MMF diagram technique［J］.IEEE Transactions on Industry App lications，1996，32(3):569－576.

［10］ 王秀和.永磁电机［M］.北京:中国电力出版社，2007.