新型二自由度电机的磁路模型研究

方春仁，杨文焕，吴 坚，谢 双

(上海理工大学，上海200093)

0 引 言

直线旋转电机具有直线运动、旋转运动和螺旋运动三种运动方式。由于它有多种运动状态，可以大大简化系统的机械结构，因此受到人们广泛的重视。

本文提出了一种新型混合式直线旋转步进电动机的结构，该电机旋转部分将永磁材料嵌入转子中间，直线部分定子段中间嵌入永磁材料。分析二自由度混合式步进电动机的电机结构，并分析在不同励磁电流下，电机旋转段和直线段的工作原理，依此工作原理为基础，建立电机的等效磁路网络模型，以一相绕组通电为例，对混合式步进电动机全网络进行了线性解析，进而计算电机的力移特性解析式。

1 新型电机结构及运行原理

这种新型混合式直线旋转步进电动机的定子段分为直线运动部分的定子段和旋转运动部分的定子段，如图1(a)、(b)所示;电机转子部分分为直线运动转子段和旋转运动转子段，如图1(c)、(d)所示。该电机定子和转子都是硅钢片按一定的方式叠压而成。

1.1 旋转运动的工作原理

电机旋转段的定子有8 个极，极身绕有线圈，极上有6 个小齿;转子由二段硅钢片及环形磁钢组成，硅钢片上均匀分布着50 个小齿，其中环形磁钢在二段硅钢片之间，磁钢采用轴向充磁，转子铁心上环绕有齿距和定子绕组相等的小齿，但二段转子齿相互错开半个齿位。电机旋转段剖面图如图2 所示。

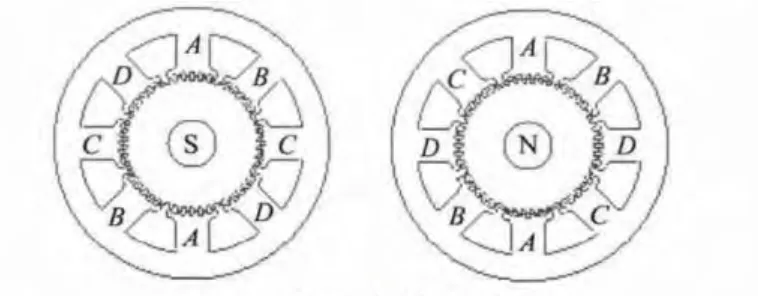
图2 电机旋转段剖面

以四相单四拍通电顺序说明工作原理，为了表述方便，将旋转段电机展开为平面示意图，如图3 所示。

当以A－B－C－D 顺序通电时，每改变一次通电状态，转子沿顺时针方向旋转1/4 个齿位，即步距角为360°/(50 ×4)=1.8°，同理当以A－D－C－B通电时，转子沿逆时针方向旋转1.8°。

1.2 直线运动的工作原理

二自由度混合式步进电动机的直线部分是基于最小磁通原理，但其结构有一定的改进。直线部分的定、动子为错位叠加的环形硅钢片，其中定子分为两段，两段定子轴向齿位在相位上错开一个齿位，永磁磁钢置于两段定子之间，永磁磁钢采用轴向充磁。

以四相单四拍通电顺序说明工作原理，为表述方便，将直线段电机展开为平面示意图，如图4 所示。

2.综合性商业体对外出租的店铺，不单只租赁不动产，还包括了提供物业管理服务，有些大型主力店铺还包括另外配置的专用机器设备、设施；如果商务谈判时不进行合理的考虑，在合同签署时统一按照租金收入来计算收取，则会导致房产税的计算依据过于增大，多交房产税的不利影响。

即当以A－B－C－D 顺序通电时，每改变一次通电状态，动子沿轴向左方向走动1/4 个齿位，同理当以A－D－C－B 通电时，动子沿轴向右方向走动1/4 个齿位，即一片定子叠片厚度。

2 电机磁路模型

磁路法的主要思想是将电机的主要结构部件用磁导表示，如电机的定动子齿、定动子轭、气隙以及永磁磁钢，以此建立电机的等效磁路模型，从而将电机的磁场问题转化成电机模型的磁路求解。

二自由度混合式步进电动机分为旋转段和直线段，由其工作原理可知，两段模型的磁路是相对独立的闭合回路，故可分开建立电机的旋转磁路模型和直线磁路模型。

建立电机的旋转部分的磁路模型图，取A 相绕组下定、转子齿对齐时建立磁网络方程，由其磁通的流通路径可得出如图5 所示的磁路简意图。

定子每相支路磁导由定子极身磁导、定转子齿间气隙磁导和转子轭磁导组成，两段转子中间为永磁体磁导。永磁体磁导可等效为一个恒定的磁势源和一个恒定的内磁导相串联而成的励磁源，它向外磁路稳定地提供磁势。

建立电机直线部分的磁路模型图，由于直线部分模型不便于用2D 的磁路模型直观地展示其磁路图，为此，建立三维的磁路模型图，为便于观察，将各相的一对极合并成一个磁路支路，如图6 所示。

定子每相支路磁导由定子极身磁导、定动子齿间气隙磁导和动子轭磁导组成，两段定子中间为永磁体磁导。永磁体磁导可等效为一个恒定的磁势源和一个恒定的内磁导相串联而成的励磁源，它向外磁路稳定地提供磁势。

3 磁路模型计算

依据图5 和图6 的电机磁路模型可知，该电机的旋转段和直线段等效磁路的结构类似，区别仅在于旋转段永磁磁钢的等效磁导在转子段，而直线段等效磁钢的等效磁导在定子段，但是，两者的磁导均在电机的主磁路中，且永磁磁导与定动子齿间气隙无关，由此，采用齿层比磁导法，可建立相同的等效磁路模型，如图7 所示。

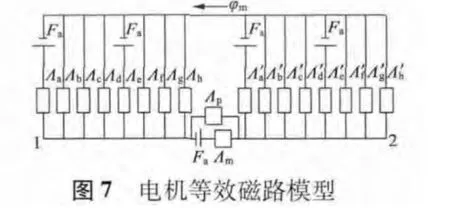
当定子绕组无励磁且只考虑齿层齿导时，即绕组励磁磁势为零，对应电机面向永磁磁钢S 段、N 段的各个齿层磁导如下:

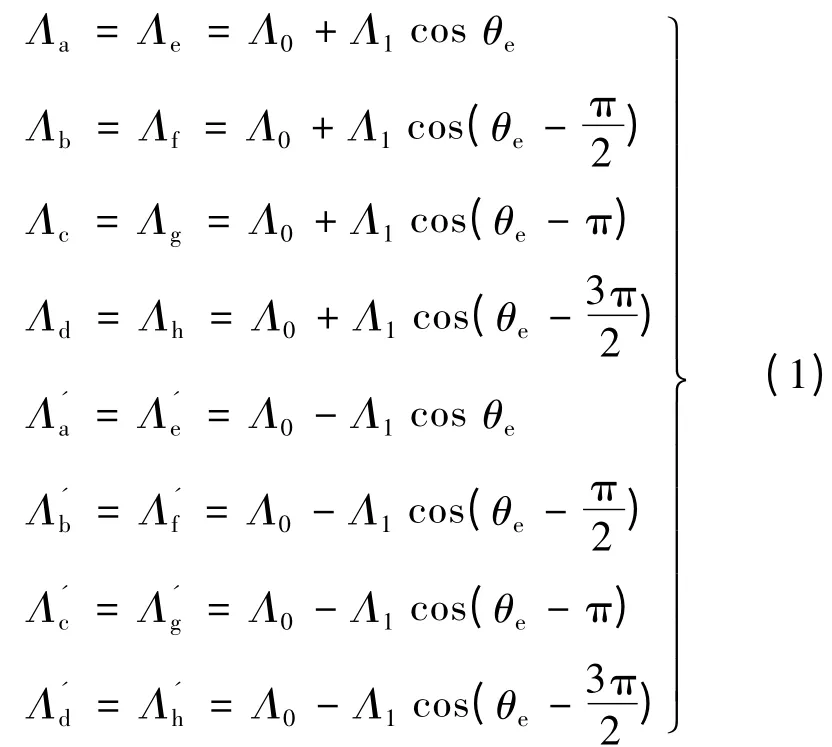
式中:Λ0为定子极身磁导;Λ1为定、转子齿相对时的最大等值磁导;θe为定、转子中心线间的电角度。由图7 结合式(1)可得出磁钢两段的外部磁路总磁导分别:

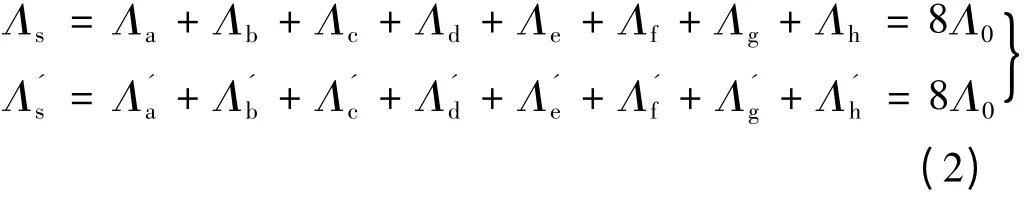
外部磁路的总磁导Λ:

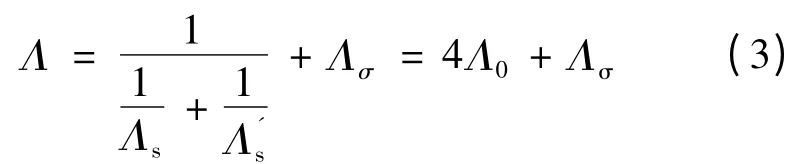
式中:Λσ为漏磁导。由式(3)可知，外部磁路总磁导一定，故磁钢工作点和总磁通与转子位置角无关，可求得各个极的磁通:

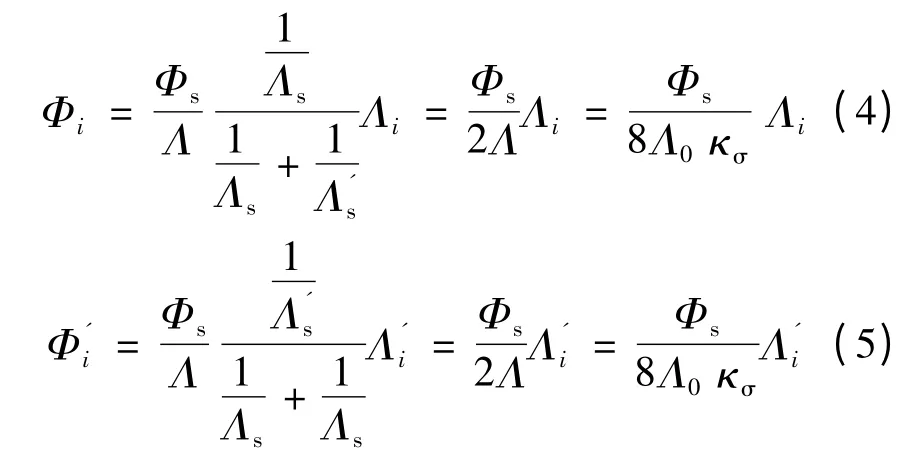
式中:κσ为磁路漏导系数。依据式(4)～式(6)建立各相总磁通表达式ΦI(I=A，B，C，D，E，F，G，H)。

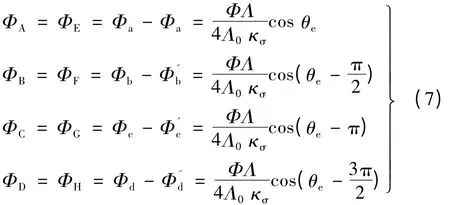
由式(7)知，当磁路网络中定子绕组无励磁且只考虑齿层磁导时，各相磁通是转子位置角的函数。

依此讨论A 相绕组励磁时，动子的转矩特性求解。对图7 中所列节点1、2 建立节点磁压方程:

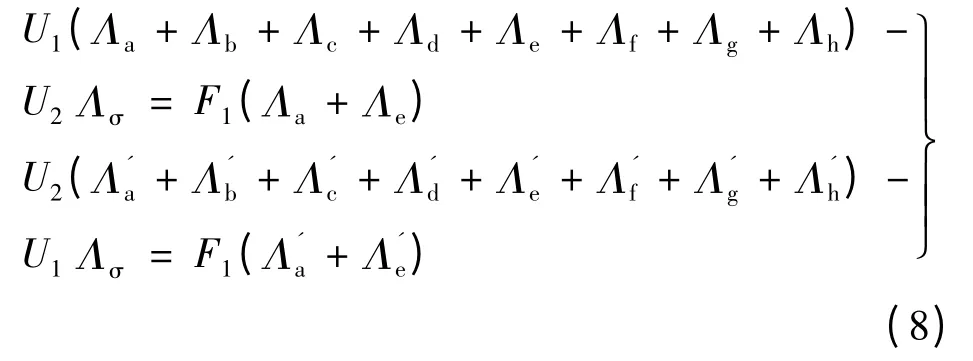
对式(8)求解，可得1、2 两点间的磁压降:

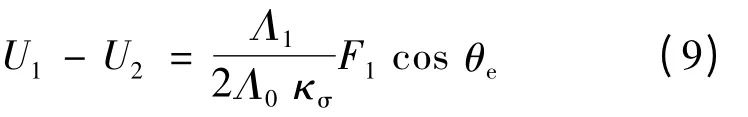
由此分析可知，当A 相绕组单独励磁时，定子磁势在磁钢两段产生的磁压降:

转子磁钢与A 相绕组交链的总磁链:

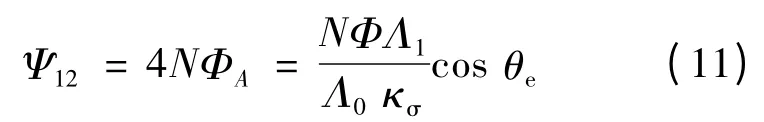
由式(11)可知，定子产生的磁共能:

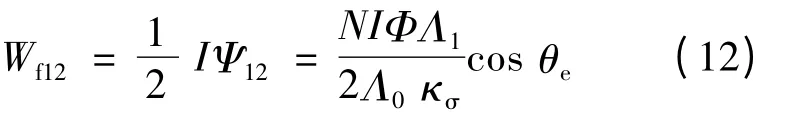
设A 相绕组励磁在磁钢中产生的磁通为ΔΦ，在转子磁钢中产生的磁共能:

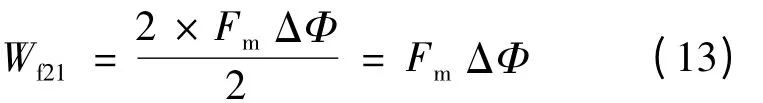
由于永磁磁钢的退磁曲线为直线，可得关系式:

联立式(13)和式(14)可得转子磁钢的磁共能:

则电机内的总磁共能:

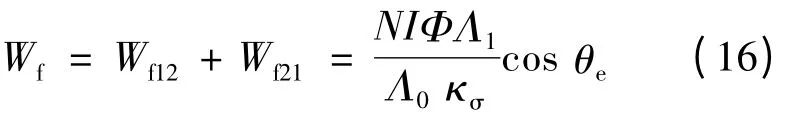
由虚位移原理可得A 相通电时的静态转矩:

式中:N 为定子每个大极上的绕组匝数;I 为相电流;Zr为转子齿数;θ 为定转子齿中心线间夹角的机械角度，且θe=Zrθ。

4 结 语

齿层比磁导法适用于直线旋转步进电动机静态性能的试验分析。该方法有效地计及了直线旋转步进电动机运行时的铁心饱和，因而显著地提高了性能数值分析的准确程度，能满足直线旋转步进电动机工程计算的要求。

［1］ 王宗培，姚宏.步进电机设计和计算方法的研究［M］.南京:东南大学出版社，1994.

［2］ 杨文焕，怡勇，赵天明.双径向磁场反应式直线旋转步进电机:中国，2008100427463［P］. 2008－10－01.

［3］ 汪玉凤.永磁感应子直线步进电机的力移特性［C］//直线电机与自动化——2002 年全国直线电机学术年会论文集. 中国电工技术学会直线电机专委会，2002.

［4］ 黄建科. 步进电机在自动线中的应用［J］. 制造业自动化，2009，31(8):135－137.

［5］ 葛宝明，赵楠.横向磁场直线开关磁阻电机及其控制系统［J］.中国电机工程学报，2007，27(33):22－29.

［6］ 杨正林，全力.直线步进电机力移特性的非线性数值分析［J］.江苏工程学报，1991，12(4):103－109.

［7］ 于学海.横向磁场直线旋转开关磁阻电机的研究［D］.北京交通大学，2006:9－40.

［8］ TAKEMOTO M，CHIBA A，AKAGI H，et al. Radial force and torque of a bearingless swithched reluctance motor operating in region of magnectic saturation［J］. IEEE Transactions on Industry Applications，2004，40(1):103－112.