地铁常用隧道杂散电流场三维有限元模拟＊

王果，裴潇湘

（兰州交通大学 自动化与电气工程学院，甘肃 兰州730070）

在地铁直流牵引供电系统中，电流经钢轨流回牵引变电所负极。由于钢轨对地并不能做到完全绝缘，会使得一小部分电流由钢轨流向大地，并在大地通过某条路径流回牵引变电所负极，这些电流被称为杂散电流。杂散电流会对隧道结构钢筋以及周围埋地金属管线产生腐蚀危害，严重时甚至会威胁到人身安全［1］。因此对杂散电流的研究受到国内外的重视。

目前对地铁杂散电流场的模型研究主要是Baeckamnn等［2－4］建立的以牵引电流、轨道电阻和轨地过渡电阻为变量的电路元件模型；Pham等［5－6］建立的电场模型；Brenna等［7－9］建立的二维地铁隧道有限元模型。这些模型均能够宏观定性地确定地铁杂散电流的分布规律。电路元件模型将地铁系统模型简化为电阻网络模型和电场模型从理论推算地下电位，这些模型对复杂的隧道类型和地质环境并不能进行模拟；胡云进建立的二维有限元模型将地铁系统简化，没有考虑隧道类型、隧道材料对杂散电流的影响；Brenna等［7－8］只建立盾构型隧道模型，得出杂散电流腐蚀发生在电流流出处的结论，而且没有计算隧道周围大地的杂散电流情况。由于在一般情况下，行车区间地铁隧道类型是盾构型结构，在车站处是明挖矩形结构［10］，所以考虑隧道类型对杂散电流场的影响对杂散电流的防护范围及重点防护对象具有重要的意义。本文采用有限元方法并以实际地铁隧道尺寸和埋深建立矩形隧道模型和盾构型隧道模型［11－12］。

1 地铁隧道杂散电流场模型

1.1 几何模型

根据实际地铁隧道尺寸和埋深，图1所示为地铁杂散电流场计算域截面图。图中土壤域100m×60m，计算长度1 000m，隧道埋深10m。根据隧道结构类型不同，地铁常用隧道结构如图2所示，图2（a）为矩形隧道结构图，图2（b）为盾构型隧道结构图，隧道结构各部分尺寸在图中标示。为了简化计算，钢轨截面等效为2个0.15m×0.176 m的长方形，且2根钢轨相距1.435m。

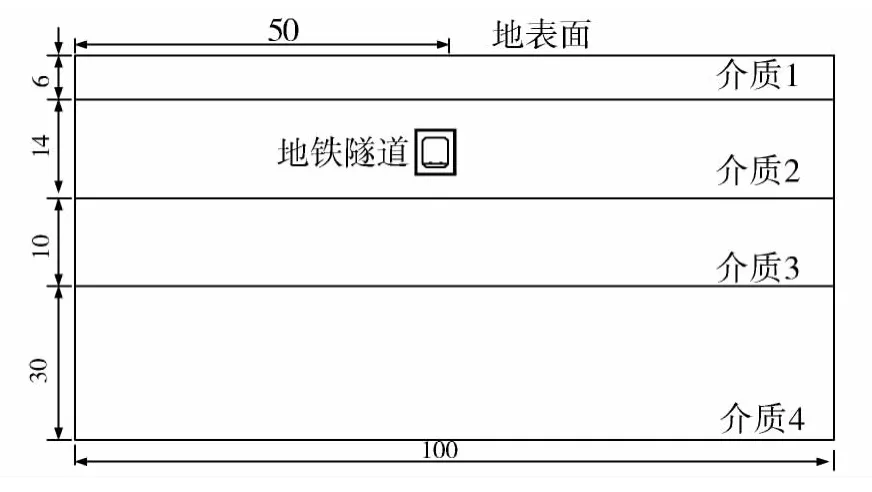
图1 地铁杂散电流场计算域截面图（单位：m）Fig.1 Sectional view of computional domain of subway stray current field（m）

1.2 数学模型

根据欧姆定律得三维恒定电流场的电流密度分量为：

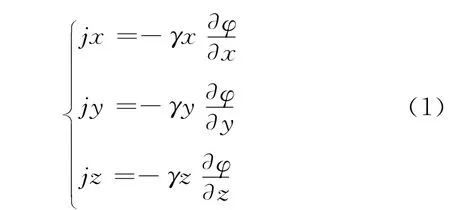
式中：jx，jy和jz分别表示x，y和z方向上的电流密度分量（A／m－2）；γx，γy和γz分别表示x，y和z方向上的电导率（S／m－1）；φ表示电位（V）。

在x，y和z方向上电流连续性方程为：

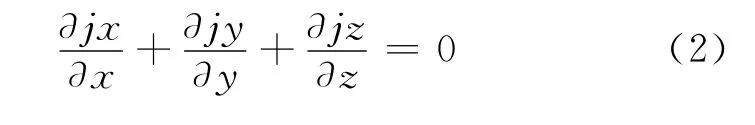
图2 常用地铁隧道结构图（单位：m）Fig.2 Structure of subway tunnel

将式（1）代入式（2）中得三维地铁杂散电流场的电位基本方程为：

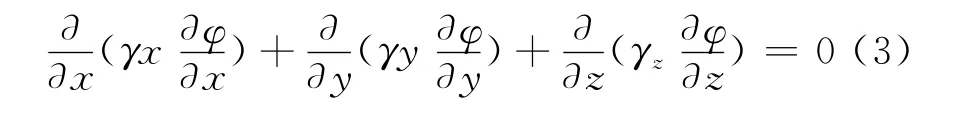
对于恒定电流场，只需列出边界条件即可，式（3）的定解条件为：

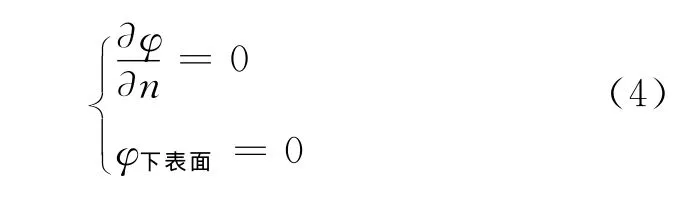
2 地铁隧道杂散电流场有限元仿真分析

有限元法可以求解计算域边界形状和地质条件复杂多变的情况，也可以处理各种类型的边界条件和模拟由多种材料构成的结构。故本文分别在均匀土壤介质和分层土壤介质中建立不同的隧道类型进行杂散电流场有限元仿真计算并进行对比分析。

2.1 均匀土壤介质杂散电流场分析

在均匀土壤介质中，图1所示的介质1－4为同一介质。根据隧道结构的不同，矩形隧道的2层衬砌材料分别为喷射混凝土和钢筋混凝土，而盾构型隧道的管片材料只为钢筋混凝土。计算所用参数如表1所示。

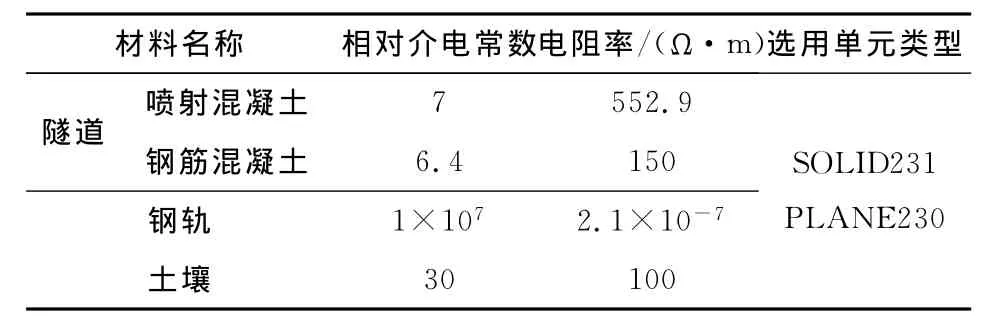
表1 均匀土壤介质仿真参数说明Table 1 Simulation parameters of homogeneous soil media

为了分析不同牵引电流在不同隧道类型的情况下对杂散电流分布的影响，分别在每根钢轨一端加载不同的电流值。由于加载到钢轨上的电流几乎全部泄露到地下，即为杂散电流，按流入地下的杂散电流为牵引电流的5%算，每根钢轨加载电流为2.5%。故分别在每根钢轨一端加载10，20，50和100A的电流值。由于计算结果中不同加载电流对应的等值线图一致，不同的只是等值线上的数值，故以加载电流10A为例，加载电流为10 A时电场电位等值线图如图3所示，图3（a）为矩形隧道电场电位等值线图，图3（b）为盾构型隧道电场电位等值线图。隧道附近电场电位等值线图如图4所示，图4（a）为矩形隧道附近电场电位等值线图，图4（b）盾构型隧道附近电场电位等值线图。

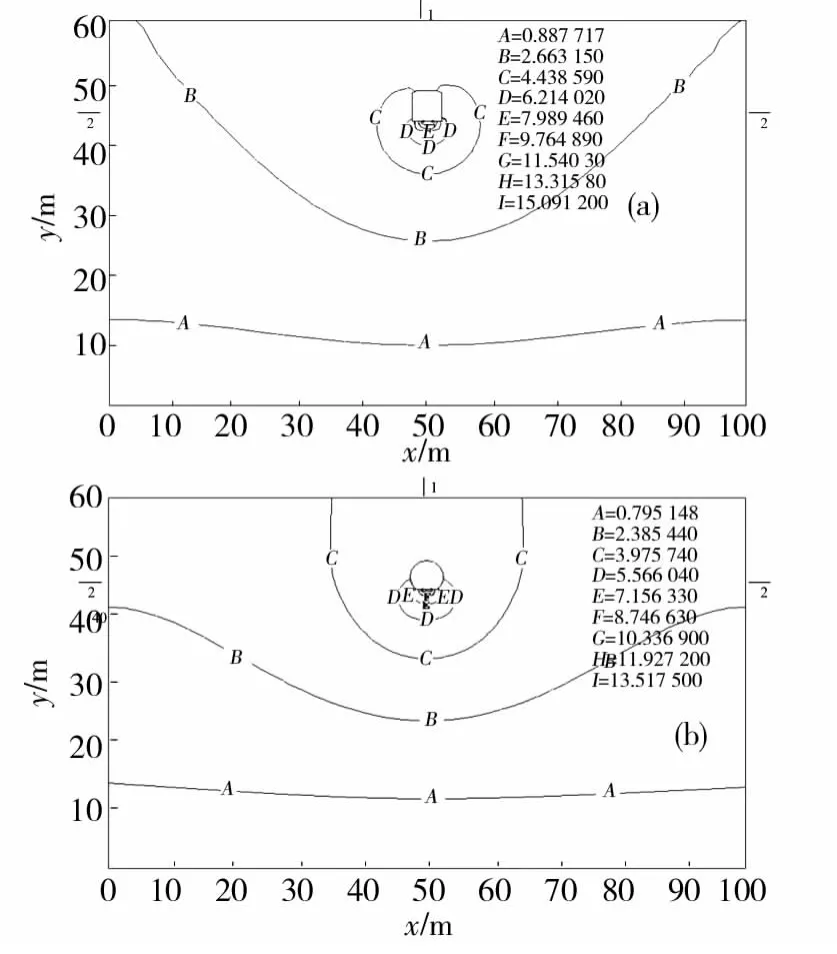
图3 均匀土壤介质中电场电位等值线图（10A）Fig.3 Electric potential contours in homogeneous soil media of 10A

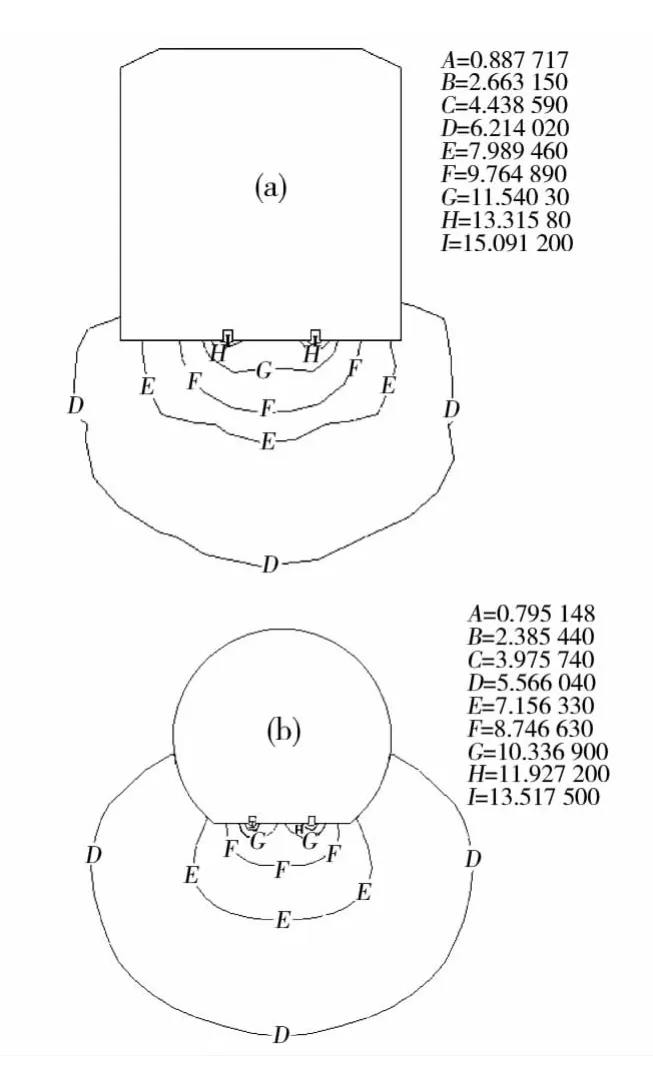
图4 均匀土壤介质中隧道附近电场电位等值线图（10A）Fig.4 Electric potential contours of neighboring tunnel in homogeneous soil media of 10A

由图3和图4的分析可知：在均匀土壤介质中，地铁矩形隧道结构和盾构型隧道结构有限元仿真的计算结果均为：钢轨及钢轨至周围地下环境的电位是逐渐降低的，这表明离钢轨越远杂散电流强度越低。

为了更详细比较分析不同隧道对杂散电流分布的影响，本文将模型划分3个剖面：分别为如图3所示的1－1剖面即穿过左侧钢轨中心的纵剖面；2－2剖面即穿过钢轨底面的横切面和钢轨面。选取1－1剖面z＝0的路径，距离地表面不同深度的电位曲线图如图5所示，图5（a）为矩形隧道1－1剖面电位曲线图，5（b）为盾构型隧道1－1剖面曲线图；选取2－2剖面z＝0的路径，距离左侧土壤边界不同位置的电位曲线图如图6所示，图6（a）为矩形隧道2－2剖面电位曲线图，6（b）为盾构型隧道2－2剖面曲线图；钢轨面钢轨上的电位曲线图如图7所示，图7（a）为矩形隧道钢轨电位曲线图，7（b）为盾构型隧道钢轨曲线图。

图3－7的电位曲线图表示矩形隧道和盾构型隧道在不同的牵引电流下，钢轨及钢轨到周围地下环境的电位分布情况，其电位的最大和最小值如表2所示，这里矩形隧道结构和盾构型隧道结构的1－1剖面电位最小值均为0。由图5－7和表2得出在均匀土壤介质中：

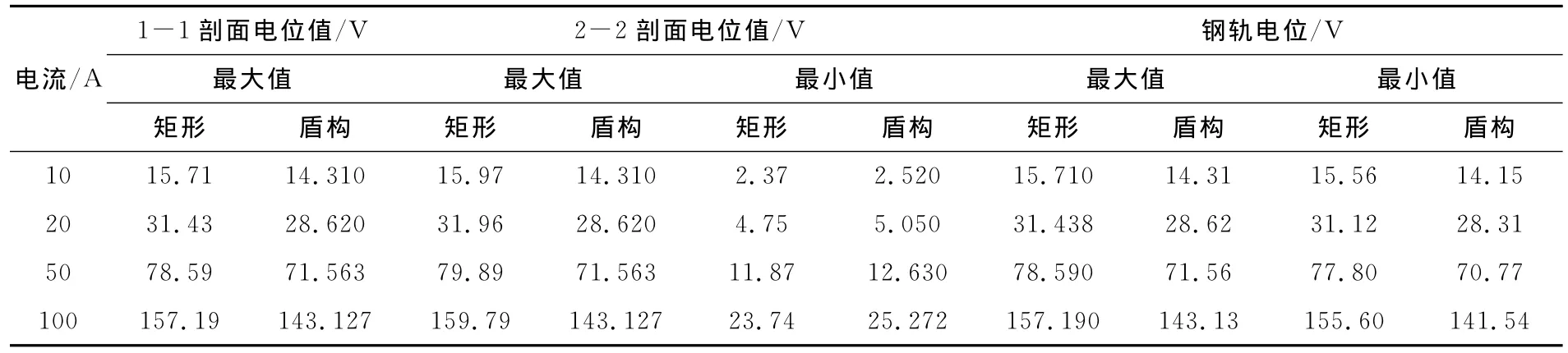
表2 钢轨和钢轨到周围地下环境电位分布情况Table 2 Poential distribution of the railway and railway to the surrongding undergrond environment

图5 均匀土壤介质中1－1剖面电位曲线图Fig.5 Potential curve of 1－1in homogeneous soil media

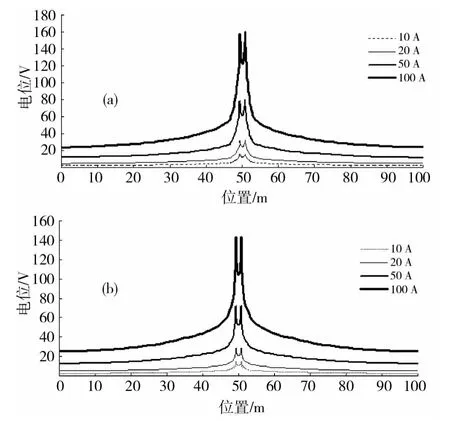
图6 均匀土壤介质中2－2剖面电位曲线图Fig.6 Potential curve of 2－2in homogeneous soil media

（1）无论是矩形隧道还是盾构型隧道钢轨及钢轨周围地下环境的电位随着加载电流的增大而增大；

（2）1－1剖面中，矩形隧道的最大电位比盾构型隧道的最大电位大，最小电位均为0；

（3）2－2剖面中，矩形隧道的最大电位比盾构型隧道的最大电位大，但是最小电位比盾构隧道小；

（4）钢轨上，矩形隧道的最大最小电位均比盾构型隧道大。

因此能够说明矩形隧道比盾构型隧道向外泄漏的杂散电流少。

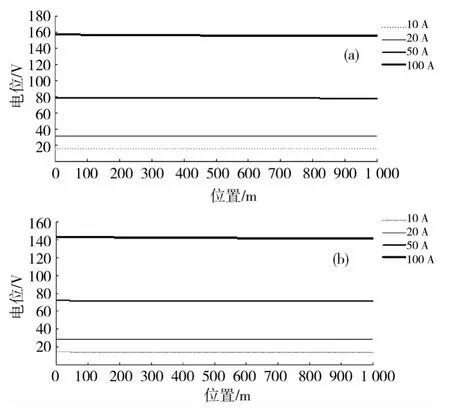
图7 均匀土壤介质中钢轨电位等值线图ig.7 Potential curve of railway in homogeneous soil media

2.2 分层土壤介质杂散电流场分析

在分层土壤介质中，图1所示的介质1－4为不同介质。建模仿真所选用的单元类型、隧道参数和钢轨参数均不变，如表3所示分层土壤介质参数［13］。

表3 各土层电阻率参数Table 3 Resistivity Parameters of each Soil

同样地，分别在每根钢轨一端加载10，20，50和100A的电流值。计算结果为不同加载电流对应的等值线图一致，不同的只是等值线上的数值。故仍以加载电流10A为例，加载电流为10A时电场电位等值线图如图8所示，图8（a）为矩形隧道电场电位等值线图，图8（b）为盾构型隧道电场电位等值线图。隧道附近电场电位等值线图如图9所示，图9（a）为矩形隧道附近电场电位等值线图，图9（b）盾构型隧道附近电场电位等值线图。

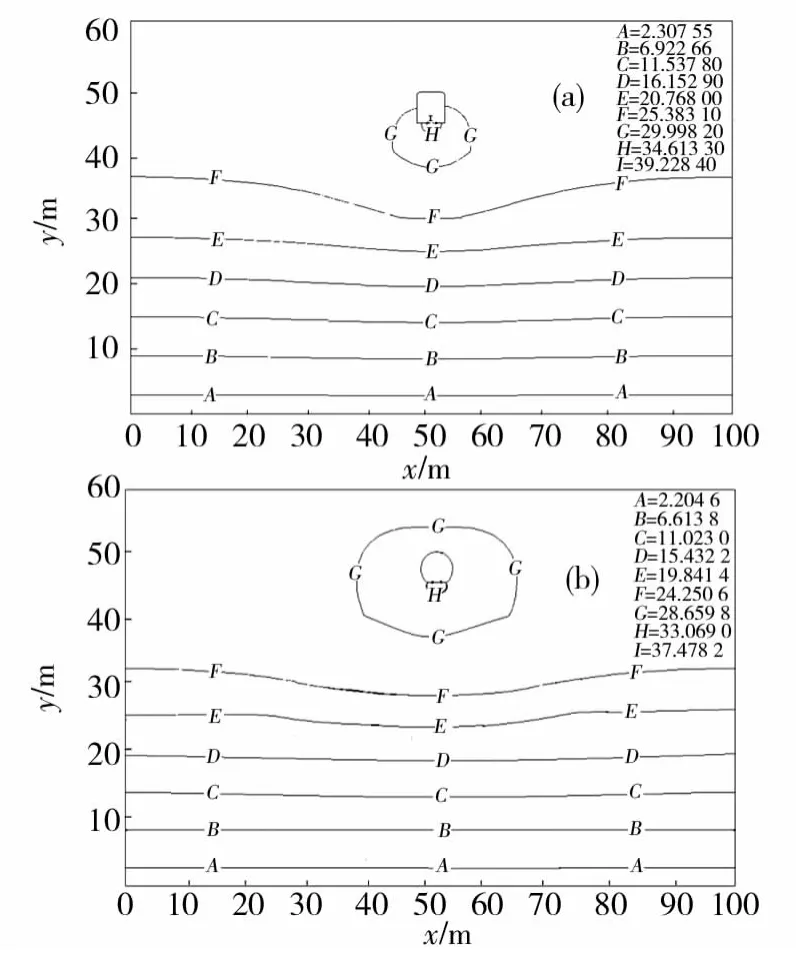
图8 分层土壤介质截面电场电位等值线图（10A）ig.8 Electric potential contours in stratified soil media of 10A

由图8和图9可以看出，在分层土壤介质中，地铁矩形隧道结构和盾构型隧道结构有限元仿真出的电位分布规律与均匀土壤介质中的电位分布规律一致。

同样地，在分层土壤介质中将三维模型划分的3个剖面同均匀分层土壤介质一致。如图10所示为1－1剖面选取z＝0路径时，距离地表面不同深度的电位曲线图，图10（a）为矩形隧道1－1剖面电位曲线图，10（b）为盾构型隧道1－1剖面曲线图；如图11所示为2－2剖面选取z＝0路径时，距离左侧土壤边界不同位置的电位曲线图，图11（a）为矩形隧道2－2剖面电位曲线图，11（b）为盾构型隧道2－2剖面曲线图；如图12所示为钢轨面钢轨上的电位曲线图，图12（a）为矩形隧道钢轨电位曲线图，12（b）为盾构型隧道钢轨曲线图。图10－12表示矩形隧道和盾构型隧道在不同的牵引电流下，钢轨及钢轨到周围地下环境的电位分布情况，其电位的最大和最小值如表4所示。这里矩形隧道结构和盾构型隧道结构的1－1剖面电位最小值均为0。

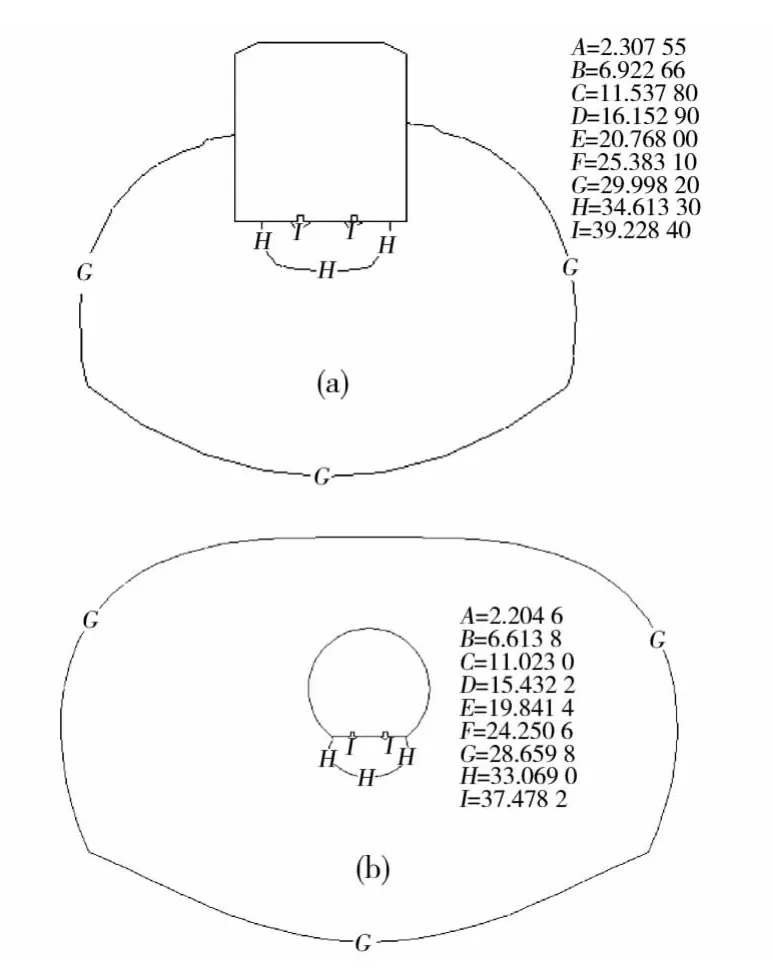
图9 分层土壤介质隧道附近电场电位等值线图Fig.9 Electric potential contours of neighboring tunnel in stratified soil media of 10A

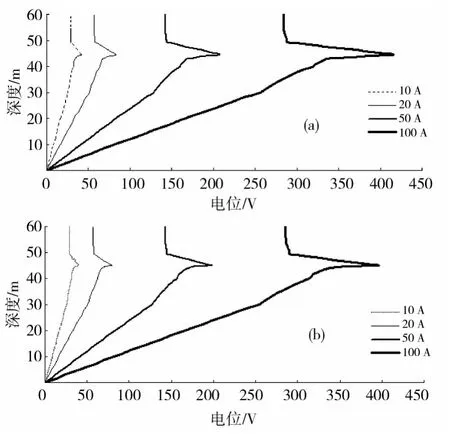
图10 分层土壤介质1－1剖面电位曲线Fig.10 Potential curve of 1－1in stratified soil media

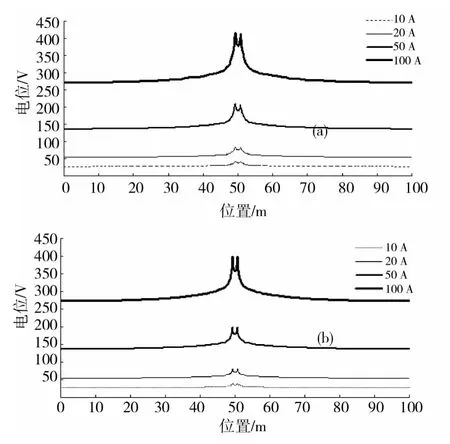
图11 分层土壤介质2－2剖面电位曲线Fig.11 Potential curve of 2－2in stratified soil media

图12 分层土壤介质中钢轨电位曲线Fig.12 Potential curve of railway in stratified soil media

由图8－12和表4可以得出矩形隧道与盾构型隧道在分层土壤介质与均匀土壤介质中，不同加载电流对杂散电流的影响规律一致。

矩形隧道与盾构型隧道无论是在均匀土壤介质中还是在分层土壤介质中，钢轨和钢轨到周围地下环境的电位都是呈衰减趋势的。在同一加载电流10A时，均匀土壤介质和分层土壤介质在剖面1－1对比如表5所示，剖面2－2如表6所示，钢轨方向如表7所示。

由表5可以清晰的看出，同一隧道结构时，剖面1－1在54－60m区域均匀土壤介质的电压降明显大于分层土壤介质，在30－40m区域均匀土壤介质的电压降明显小于分层土壤介质。这主要是由于电压降主要集中在电阻率ρ（ρ1＜ρ2＜ρ3＜ρ4）比较高的区域。

在不同隧道结构时，剖面1－1在54～60m区域矩形隧道的电压降大域盾构型隧道，在30～40m区域矩形隧道的电压降小于盾构型隧道，这表明矩形隧道的绝缘性比盾构型隧道好。

由表6所示在剖面2－2，同一隧道结构时，均匀土壤介质的电压降与分层土壤介质电压降相差不多，原因是由于本文是水平土壤分层，在水平剖面方向电阻率没有变化。

在不同隧道结构时，矩形隧道的最大电位比盾构型隧道的最大电位大，最小电位比盾构隧道小，电压降比盾构隧道大，这表明矩形隧道向外泄漏的杂散电流小。

由表7所示在钢轨方向，同一隧道结构时，均匀土壤介质的电压降与分层土壤介质电压降相等，原因与上述一致。

表4 钢轨和钢轨到周围地下环境电位分布情况Table 4 Poential distribution of the railway and railway to the surrongding undergrond environment

表5 剖面1－1均匀土壤介质和分层土壤介质的对比Table 5 Comparison of homogeneous soil media and stratified soil media on 1－1

在不同隧道结构时，矩形隧道的电压降与盾构型隧道相等。

从以上分析可知电阻率越大，绝缘性越好，杂散电流泄漏到周围土壤的范围越小，但是钢轨、隧道附近的电位也越大。

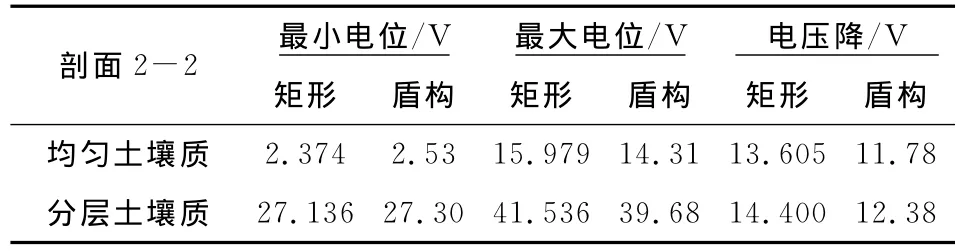
表6 剖面2－2均匀土壤介质和分层土壤介质的对比Table 6 Comparison of homogeneous soil media and stratified soil media on 2－2

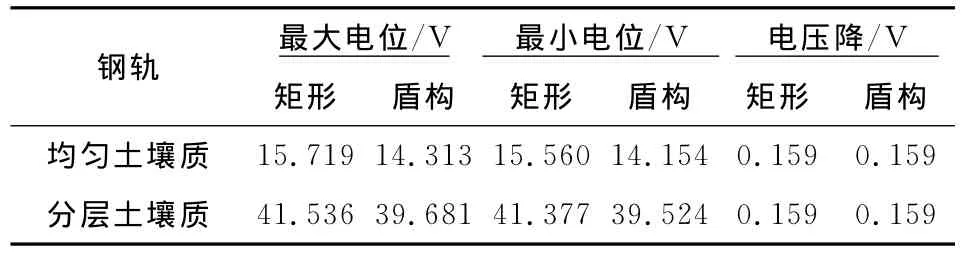
表7 钢轨均匀土壤介质和分层土壤介质的对比Table 7 Comparison of homogeneous soil media and stratified soil media on railway

3 结论

（1）随着牵引电流值的增大，钢轨及钢轨周围介质的电位升高，泄漏电流增大。减小牵引电流能够有效的减少杂散电流；

（2）由均匀土壤介质和分层土壤介质的电位分布对比分析可知，电阻率越大，向外泄漏的杂散电流越少，加大钢轨周围介质电阻率及隧道电阻率可以有效减小杂散电流影响范围；

（3）由两种隧道结构的电位分布对比分析可知：不同隧道周围相同位置处的电位不同；在钢轨加载电流和隧道周围地质条件相同的情况下，矩形隧道比盾构型隧道向外泄漏的杂散电流少；车站处比行车区间向外泄漏的杂散电流少。

［1］李威.地铁杂散电流腐蚀检测与防护技术［M］.徐州：中国矿业大学出版社.

LI Wei.Stray current corrosion detection and prevention technology in subway［M］.Xuzhou：The Publishing House of China University of Mining and Technology，2004.

［2］Baeckamnn W V.阴极保护手册［M］.胡士信，译.北京：化学工业出版社，2005.

Baeckman W V.Cathodic protection guide［M］.HU Shixin，trans.Beijing：The Publishing House of Chemical Industry，2005.

［3］牟龙华.排流网情况下地铁迷流分布规律的研究［J］.铁道学报，2007（3）：47－51.

MOU Longhua.Metro stray current distribution with current drainageNet［J］.Journal of the China Railway Society，2007，29（3）：47－51.

［4］刘 燕，王京梅.地铁杂散电流分布的数学模型［J］.工程数学学报，2009（4）：571－576.

LIU Yan，WANG Jingmei.Mathematical model of distribution of metro stray current［J］.Chinese Journal of Engineering Mathematics，2009（4）：571－576.

［5］Pham K D，Thomas R S，Stinger W E.Analysis of stray current，track－to－earth potentials ＆substation negative grounding in DC traction electrification system［C］／／IEEE／ASME Join Rail Conference，2001.

［6］庞原冰，李群湛.电场杂散电流模型讨论［J］.重庆工程学报，2007，21（11）：110－114.

PANG Yuanbing，LI Qunzhan.Discussions on metro＇s stray current model［J］.Journal of Chongqing Institute of Technology，2007，21（11）：110－114.

［7］Brenna M，Dolara A，Leva S，et al.Effects of the DC stray currents on subway tunnel structures evaluated by FEM analysis［J］.IEEE Power and Energy Society General Meeting，2010.

［8］Alberto Dolara，Federica Foiadelli，Sonia Leva.Stray Current Effects Mitigation in Subway Tunnels［J］.In IEEE Transactions on Power Delivery，2012，27（4）：125－131.

［9］胡云进，钟振，方镜平.地铁杂散电流场的有限元模拟［J］.中国铁道科学，2011，32（6）：129.

HU Yunjin，HONG Zhen，FANG Jingping.Stray current field of finite element analysis in subway［J］.China Railway Science，2011，32（6）：129.

［10］姜晨光.地铁建设简明技术手册［M］.北京：化学工业出版社，2011.JIANG Chenguang.Subway construction condensed Technical Manual［M］.Beijing：The Publishing House of Chemical Industry，2011.

［11］王磊，李珊，周陶勇.基于ANSYS的几种建模方法的探讨［J］.现代机械，2006（3）：51－53.

WANG Lei，LI Shan，ZHOU Taoyong.The discussing of building model based on ANSYS［J］.Modern Machinery，2006（3）：51－53.

［12］王世山，王德林，李彦明.大型有限元软件ANSYS在电磁领域的使用［J］.高压电器，2006，38（3）：27－33.

WANG Shishan，WANG Delin，LI Yanming.Using software ANSYS to analyze electro magnetic process［J］.High Voltage Apparatus，2006，38（3）：27－33.

［13］肖裕生，施春华.南京地区第四系主要地层类型及分层探讨［J］.南京大学学报，2008，7（2）：60－65.

XIAO Yusheng，SHI Chunhua.On the division of the quaternay in the Nanjing region，Eastern China［J］.Journal of Nanjing University （Natural Science Edition），2008，7（2）：60－65.