新型体外预应力体系预应力瞬时损失试验研究＊

郭风琪，袁石沣，单智

（1.中南大学 土木工程学院，湖南 长沙410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙410075）

朔黄铁路是我国西煤东运第二大通道，为提高运输能力，计划对沿线桥梁进行提载强化。体外预应力加固法施工简便，不阻断交通，能使桥梁的受力性能得到明显改善［1］，是优先选择的方案。针对拟强化桥梁的特点和要求，采用了体外预应力体系进行加固设计。体外预应力加固系统同样存在耐久性和安全性问题，因此在设计过程中精确计算体外预应力损失值是保证强化效果的一个重要方面［2］。本试验体系的锚具、预应力束和转向器根据朔黄铁路桥梁的特点进行了特殊设计，其预应力损失情况有必要进行专项研究。体外预应力系统的应力损失包括多个关键因素，目前的研究一般将预应力损失分为瞬时损失和长期损失2类［3］。瞬时损失是指张拉预应力筋时短时间内完成的损失，包括锚固损失、摩擦损失等。长期损失是指考虑时间因素以后预应力筋的应力损失，包括混凝土的收缩徐变损失和预应力松弛损失等［4］。考虑体外预应力结构的特性及本试验的限制，本文主要研究瞬时损失，即锚固损失σl1和摩擦损失σl2。

1 理论估算公式

1.1 锚固损失σl1

体外预应力筋只在锚固端和转向器部分与梁体局部接触［5］，计算过程中可忽略钢筋反向摩擦引起的预应力损失。因此，锚固损失σl1的计算可按下式进行［6］：

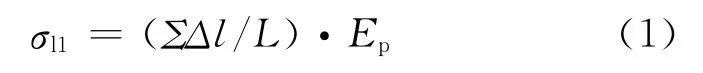
式中：ΣΔl为张拉端锚具变形和钢筋回缩值；L为张拉端至锚固端之间的有效长度；Ep为预应力筋的弹性模量。

1.2 摩阻损失σl2

根据规范σl2的计算按下式进行：

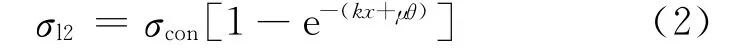
式中：σcon为预应力钢筋锚下的张拉控制应力；x为从张拉端至计算截面的管道长度；k和μ分别为管道每米局部偏差对摩擦的影响系数和预应力筋与管道的摩擦因数。对于体外索，k可值取0，θ为从张拉端至计算截面曲线管道部分切线的夹角之和，其取值可参考文献［7］。

施工过程中，由于转向器及管道安装精度不够，体外预应力筋的偏转角存在误差，考虑上述因素后公式（2）修改为：

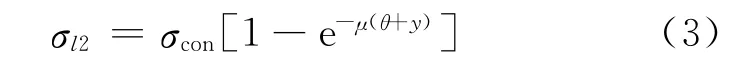
式中，y为转向器处预应力筋的偏角误差［8］。y由试验得到，数据资料不全时可近似取y＝0.04rad［9］。

2 试验设计与实施

2.1 试验设计

试验梁为24m后张预应力混凝土超低高度T梁，梁截面高1 250mm，上翼缘板宽1 950mm，下翼缘板宽1 060mm，混凝土强度C60，龄期超过5a。体外预应力筋采用4根15.2mm环氧喷涂无黏结钢绞线，强度标准值1 860MPa，钢绞线在T梁两侧对称各布置一束。为减小摩擦，每根钢绞线均用小PE层包裹后，整体用缠包带及外围PE护套包裹。整个体外预应力束直径为54mm，图1为截面示意图。沿梁纵向1／3与2／3处各设置一个转向器，转向器采用内设四氟板的三维半圆弧张口钢构件形式，如图2所示。该转向器的构造既保证了钢绞线的顺利转向，避免了应力集中现象，又可减少因加工误差带来的预应力损失。转向器通过高强螺栓与梁体横隔板相连。锚具为新型带螺帽式挤压锚，可通过螺杆和反力钢板施加预应力，如图3所示。张拉设备采用RSC－301油压千斤顶，配套手动泵体使用。考虑到数据记录的方便性与连续性，所有体外预应力筋上的应变片数据全部用IMC设备采集，IMC能够准确反应整个张拉过程有效预应力的变化情况，便于后续的数据整理分析。张拉控制应力为σcon＝0.48fptk＝892.8MPa，由于场地原因限制采用单端张拉。沿高低两侧体外预应力筋全长设5个测点，共计10个测点，每个测点分别布置2个应变片。体外预应力筋及应变片布置如图4所示。

图1 无黏结钢绞线截面图Fig.1 Section of the unbonded tendons

图2 转向器形式图Fig.2 Steering gear form

图3 锚具及千斤顶设置Fig.3 Installation of anchorage and jack

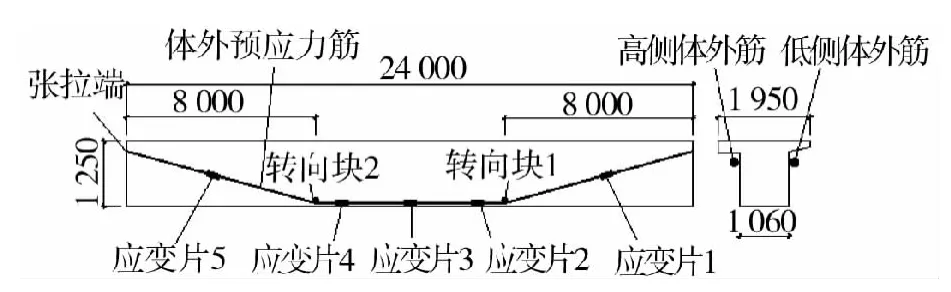
图4 体外预应力筋及应变片布置示意图ig.4 Distribution of prestressed reinforcing and steel strain gauge

2.2 试验过程

施加预应力过程中按5级加载过程依次上升油压，分级方式为20%σcon，40%σcon，60%σcon，80%σcon和100%σcon，每级加载后均需量测预应力筋伸长值，检查伸长值与理论值的偏差。根据该挤压锚的构造特点，张拉时高侧和低侧分别采用2个千斤顶同步、对称施加张拉力。由于千斤顶行程限制，在每级加载完成后都需拧紧螺帽，撤下千斤顶并相应调整反力钢板。张拉时由专人进行手动泵操作，并确保高侧和低侧油压表尽可能保持一致，以防止桥梁不均匀受力。

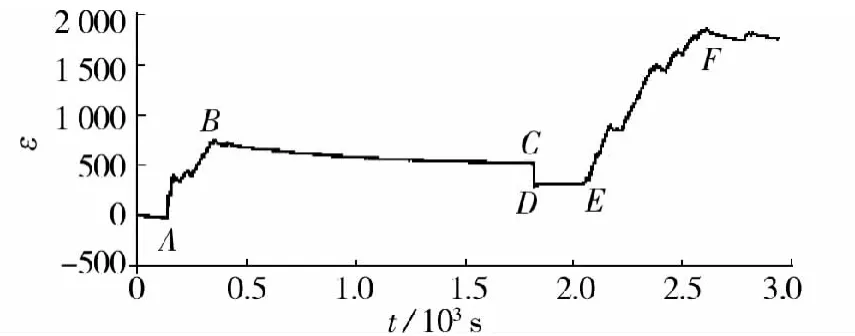
图5 预应力筋应变变化Fig.5 Strain variation

3 试验数据整理与分析

3.1 应变变化过程

受篇幅所限，本文选取IMC记录的高侧5号位置应变片的应变变化来阐述，如图5所示。从A点开始进行手动泵施加油压，由于人工操作，施加过程不稳定，AB段呈现锯齿上升状。B点达到20%σcon。BC段大致水平，有略微下降，这是达到分级控制应力时持压过程中油泵回油的缘故。CD段基本垂直下降，这是在拧紧螺帽释放千斤顶的瞬间，由于千斤顶的压力全部转由螺帽来承担时，锚具的螺丝缝隙压缩引起的锚固损失。DE段基本水平，呈现稳定状态，从E点开始进行下一级的张拉。

3.2 有效预应力值

应变片贴在预应力钢绞线的外层螺旋形钢丝上，应变片实测数据并不是严格的钢绞线轴向应变，而是外层螺旋钢丝的轴向应变，通过IMC采集的应变计算出来的应力值需进行调整。根据文献［10］的研究，预应力钢绞线拉伸时，沿外层螺旋钢丝轴线方向的应变εs小于钢绞线轴线方向的应变εc，差值百分率约为2.5%。本文通过IMC采集的应变计算时相应增大2.5%，表1为调整后高侧和低侧预应力筋各个位置的有效应力值。

表1 体外预应力筋各个位置处有效应力值Table 1 Effective stress value of externally prestressed tendons

3.3 预应力筋不同位置的应力分布

根据体外预应力筋的有效应力分别绘制高、低侧钢绞线全长应力分布如图6～图7所示。

图6 高侧体外筋有效应力分布Fig.6 Effective stress distribution in the high side

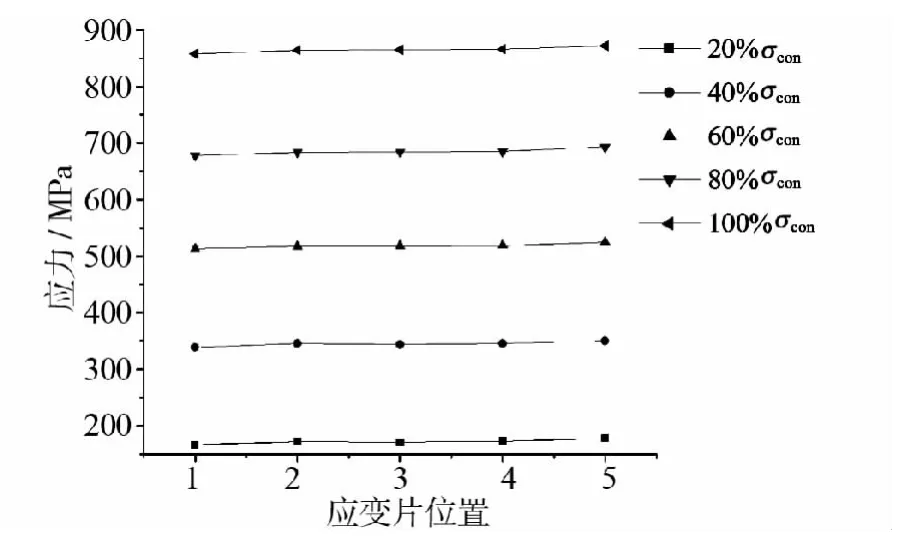
图7 低侧体外筋有效应力分布Fig.7 Effective stress distribution in the low side

理论上，5号位置靠近张拉端有效应力最大，2号，3号和4号位置处于预应力筋的水平段，理论应力值应相等且小于5号位置应力，1号位置靠近固定端，由于转向器摩擦力的影响，有效应力值最小。从图6和图7的试验数据可以看出，5号位置大于1号位置应力，与理论分析吻合，2号至4号位置应力并不是完全的水平而是略有波动，但波动值偏差为0.19%，波动很小，可以认为相等。

3.4 不同张拉阶段的预应力筋应力

不同位置应力随张拉力的增大基本呈现线弹性增大的趋势，如图8和图9所示。

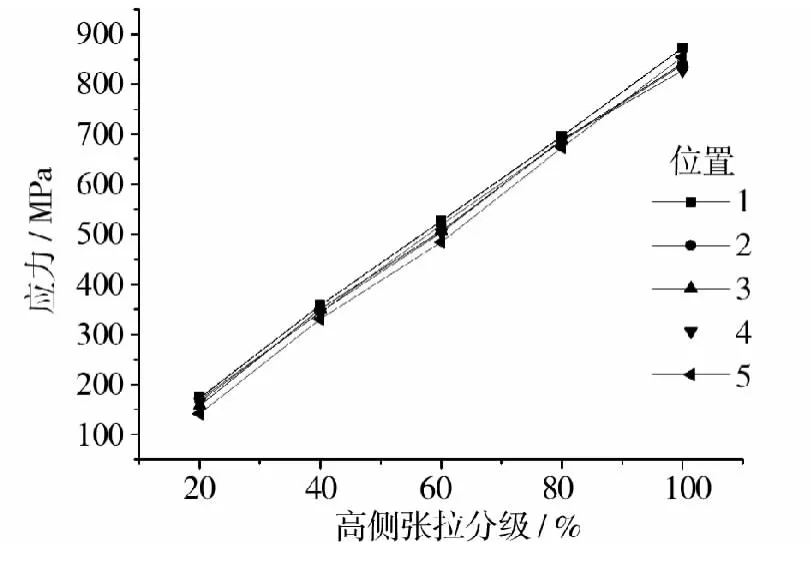
图8 高侧应力变化趋势Fig.8 Stress change trend in the high side

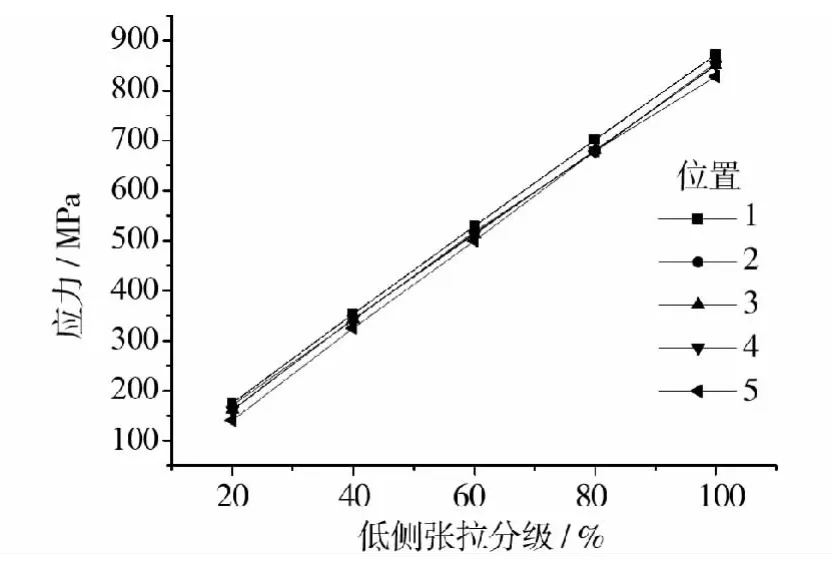
图9 低侧应力变化趋势Fig.9 Stress change trend in the low side

由图8和图9可以看出，应力随张拉等级的增加而增大的规律性比较明显。从张拉开始到张拉结束5号位置的应力都要大于1号位置，此差值σl2＝σ5－σ1即为体外预应力在2个转向器处的摩擦损失值。

3.5 体外预应力损失参数

由于张拉施工时两侧同步张拉，不用考虑分批张拉混凝土弹性压缩损失。按分项统计试验的体外预应力损失结果见表2。

表2 体外预应力损失计算结果Table 2 Loss of prestress calculation results

根据规范［6］，带螺帽锚具的螺帽缝隙Δl取1mm，按照公式（1）得出锚固损失的理论计算值σl1＝8.33MPa。而根据图5中IMC采集的CD段应力数据，锚固损失均值Δ1＝8.74MPa，两者相差0.41MPa，误差仅4.9%，与规范计算值基本吻合。

由表2可知，张拉完成后分别计算高侧和低侧5号位置与1号位置的有效应力，求得差值分别为13.6MPa和14.2MPa，二者相差不大，其均值Δ2＝13.9MPa。此处摩擦损失为2个转向器损失之和，每个转向器摩擦损失为0.8%即6.95MPa。按公式（3）反算得出无黏结体外预应力筋在使用新型转向器时摩擦因数μ为0.063，低于规范的取值0.09。

4 结论

（1）IMC不但能够实时记录大量预应力筋的有效预应力数据，而且可以直观地表现出有效预应力的发展全过程。

（2）根据试验结果，新型预应力体系计算预应力锚固损失时螺帽缝隙按规范取1mm是合理的。

（3）根据试验结果，新型预应力体系摩擦因数μ为0.063，此值低于规范的取值0.09，在本次设计予以采用。若无试验数据，偏于安全考虑，设计时此体外预应力摩擦因数μ取0.09也可行。

（4）若采用的预应力体系与现行规范不同，在有条件的情况下建议试验确定锚固损失和摩擦因数μ。

［1］徐礼华，许锋，曾浩，等.CFRP筋体外加固铁路预应力混凝土简支梁桥设计及试验研究［J］.工程力学 ，2013，30（2）：89－95.

XU Lihua，XU Feng，ZENG Hao，et al.The design and test study on prestressed railway concret beam bridge strengthened by externally draped cfrp tendons［J］.Engineering Mechanics，2013，30（2）：89－95.

［2］刘少兵.体外预应力混凝土结构耐久性防护问题的探讨［J］.铁道科学与工程学报，2007，4（4）：61－64.

LIU Shao bing.Study on durability of prestressed concrete structure with external tendons［J］.Journal of Railway Science and Engineering ，2007，4（4）：61－64.

［3］蔡建军，陶慕轩，聂建国.体外预应力组合梁桥预应力损失计算［J］.桥梁建设，2011（6）：67－70.

CAI Jianjun，TAO Muxuan，NIE Jianguo.Calculation of prestress loss of externally prestressed composite girder bridges［J］.Journal of Bridge Construction，2011（6）：67－70.

［4］兰春光，刘航，周智.基于BOTDA－FBG智能钢绞线的预应力损失监测［J］.土木工程学报，2013，46（9）：55－61.

LAN Chunguang，LIU Hang，ZHOU Zhi.Experimental investigation of prestress loss in PC beams based on BOTDA／FBG smart steel strands［J］.China Civil Engineering Journal，2013，46（9）：55－61.

［5］张连普，刘庆仁.刚混组合梁桥体外预应力摩阻损失试验分析［C］／／第十六届全国桥梁学术会议论文集（下册）.2004：805－809.

ZHANG Lianpu，LIU Qingren.Externally prestressed friction loss test analysis of steel－concrete composite beam［C］／／The 16th national conference on academic bridge（part ii）.2004：805－809.

［6］JTG／T522－2008，公路桥梁加固设计规范［S］.JTG／T522－2008，Specifications for strengthening design of highway bridges［S］.

［7］陈晓宝.预应力混凝土结构中空间索线筋的预应力摩擦损失计算［J］.土木工程学报，2003，36（6）：26－30.

CHEN Xiaobao.Calculation of prestress loss due to friction of prestress tendon with a profile of spatial curves［J］.China Civil Engineering Journal，2003，36（6）：26－30.

［8］胡志坚，胡钊芳.实用体外预应力结构预应力损失估算方法［J］.桥梁建设，2006（1）：73－75.

HU Zhijian，HU Zhaofang.Practical method for estimating the loss of prestress in externally prestressed structure［J］.Journal of Bridge Construction，2006（1）：73－75.

［9］Roberts Wollmann.Field measurements of prestress losses in external tendons［J］.ACI Structural Journal，1996，93（5）：595－601.

［10］亢景付，艾军.用应变片测定钢绞线张拉力的理论修正［J］.建筑技术，2005，36（4）：285－286.

KANG Jingfu，AI Jun.Theoretical revision of tensioning force of steel strand measured with resistance strain gages［J］.Architecture Technology，2005，36（4）：285－286.