工字型夹层板弱方向抗弯性能研究*
2014-01-04朱木锋陆铁坚宋宁王鹏皓杨诗龙
朱木锋,陆铁坚,宋宁,王鹏皓,杨诗龙
(1.江西省交通工程质量监督站,江西 南昌330009;2.中南大学 土木工程学院,湖南 长沙410075)
夹层板结构是由上表层板和下表层板以及夹在它们之间的夹芯部分组成。上下表层板一般是钢板,而夹芯部分则由不同形式的构件组成。在土木工程及海洋工程领域,夹芯部分通常是C型钢、Z型钢、波纹板以及V型板等。这种钢板夹层板由于具有良好的抗弯、抗冲击和抗爆炸[1]及隔声性能等,因此越来越受到重视。在钢板夹层板中,夹芯部分一般只沿着一个方向排列,因而在夹芯布置方向上,夹层板的刚度较大;而在垂直于夹芯方向上,夹层板的刚度相对较弱,尤其是抗剪刚度一般都比较小,这个方向称为弱方向。国内外关于夹层板有很多具有代表性的研究,Nordstrand[2]讨论了波纹板的弹性常数,分析夹层板的后屈服参数;Lok等[3-4]研究了三角形夹层板的等效常数;王海忠等[5]给出单跨、双跨以及三跨夹层板在均布荷载、集中荷载和温度荷载作用下,其弯曲内力与变形的计算方法;Fung等[6]也研究了Z型夹层板的等效弹性模量;在XU等[7-9]的研究中,本构模型被广泛地应用在模拟各种不同夹层板的变形响应中。赵彤等[10]通过预应力混凝土夹层板抗弯性能的研究,提出相应的开裂弯矩和极限弯矩计算公式;李华东等[11]对静水压力作用下的夹层板结构进行了研究,得到其内部结构变形和应力分布规律。潘鹏等[12]通过对钢丝网架水泥细石夹层板的水平承载力进行试验研究,考察了开洞及连接构造对板材受力性能及破坏模式的影响。查晓雄等[13]通过对夹层板的理论研究,得到不同面材夹层板抗弯承载力的统一表达形式。WANG等[14]研究了桁架夹层板在弱方向上静力抗弯下挠度计算方法,到目前为止,关于夹层板静力效应的研究很少,因此本文主要研究夹层板在弱方向的静力反应。
1 弱方向挠度理论分析
1.1 工字型夹层板的典型单元
图1所示为腹板夹层板结构,由上下表层板和夹在中间的腹板组成。表层板和腹板之间通过激光焊接连接成一个整体,焊接部位在工字型钢与表层板相连接处,焊接厚度与工字型钢腹板厚度一致。夹层板之间的腹板等间距分布,且均按一个方向布置。
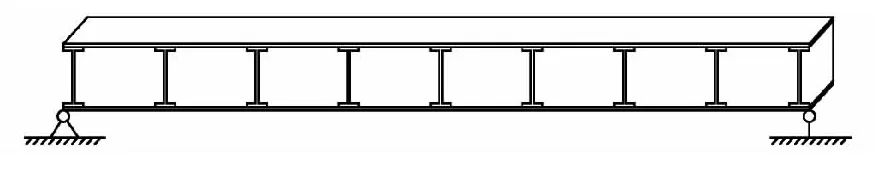
图1 腹板夹层板示意图Fig.1 AI-core sandwich panel
为了简便,将腹板夹层板的各种尺寸标注在图2中。腹板之间的间距为S,腹板高度为h,表层板的厚度为t1,工字型钢的翼缘厚度为t2、宽度为L,工字型钢腹杆的厚度为t3,腹板夹层板的宽度为B,沿着弱方向夹层板长度为C。假定x轴为腹板布置方向,z轴为夹层板发生弯曲时的挠度方向。从中拿出一个典型单元进行分析,如图2所示。
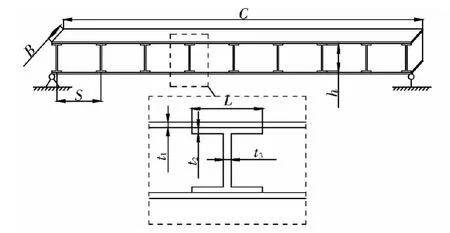
图2 腹板夹层板与典型单元Fig.2 AI-core sandwich panel and a typical segment
取出一个单元进行受力分析,先假设单元左侧弯矩值大小为M,由于沿夹层板长度方向,弯矩值不断变化,所以设右侧弯矩值大小为;先设单元左侧的剪力为V,单元右侧的剪力也为V。所以该单元受到的剪力和弯曲如图3所示。

图3 单元受力Fig.3 Internal forces of the typical segment
由图3可以看出,先观察左侧弯矩,弯矩作用于单元使上表层板受到压力,使下表层板受到拉力,同样,右侧弯矩作用于单元使上表层板受到压力,使下表层板受到拉力。因此,可以做一个等效代换,代换方法是:作用于单元左侧的弯矩M可等效为作用于该单元上下表层板所受的一对大小相等,方向相反的轴力N,作用于单元右侧的弯矩M+ΔM可等效为作用于该单元上下表层板所受的一对大小相等,方向相反的轴力N+ΔN,转化结果如图4所示。

图4 单元受力Fig.4 Internal forces of the typical segment
当腹板夹层板承受跨中静力作用时,腹板夹层板中每个典型单元的变形类似,即假定相邻单元之间的变形特性一致,反弯点位于上下表层板中间和腹板中间,所取单元上表层板左端位移与下表层板右端位移相等,同样下表层板左端位移与上表层板右端位移相等,由此可通过计算得到ΔM,ΔN的值:

设单元左侧上表层板所受剪力为,则下表面板所受剪力为,方向竖直向下,则板右侧上表层板所受剪力为,则下表面板所受剪力为,方向竖直向上。如果ΔV≠0,则该单元上表层板左侧端部所受剪力大于单元下表层板右侧端部所受剪力,同时可以观察到,该单元在受到弯矩和剪力的时候,结构会发生变形,上表层板与工字型钢上翼缘右端有接触,产生接触应力,设为F1;上表层板与工字型钢上翼缘左端会分离,不存在接触应力,同样,下表层板与工字型钢下翼缘左端会有接触,产生接触应力,设为F2。下表层板与工字型钢下翼缘右端分离,不存在接触应力。这样综合起来,由于力的作用,所取单元上表层板左侧位移比下表层板右端位移大。这与假定条件:所取单元上表层板左端位移与下表层板右端位移相等相矛盾,所以可得到单元上下表层板所受剪力为V/2,F1=F2,通设为F。单元受力如图5所示。

图5 单元受力Fig.5 Internal forces of the typical segment
1.2 工字型夹层板弱方向挠度计算公式推导
由单元受力变形可知:在上表层板与工字型钢上翼缘右端接触处和下表层板与工字型钢下翼缘左端接触处相对位移为0,可由此条件由位移法求得F,单元受力如图6所示。
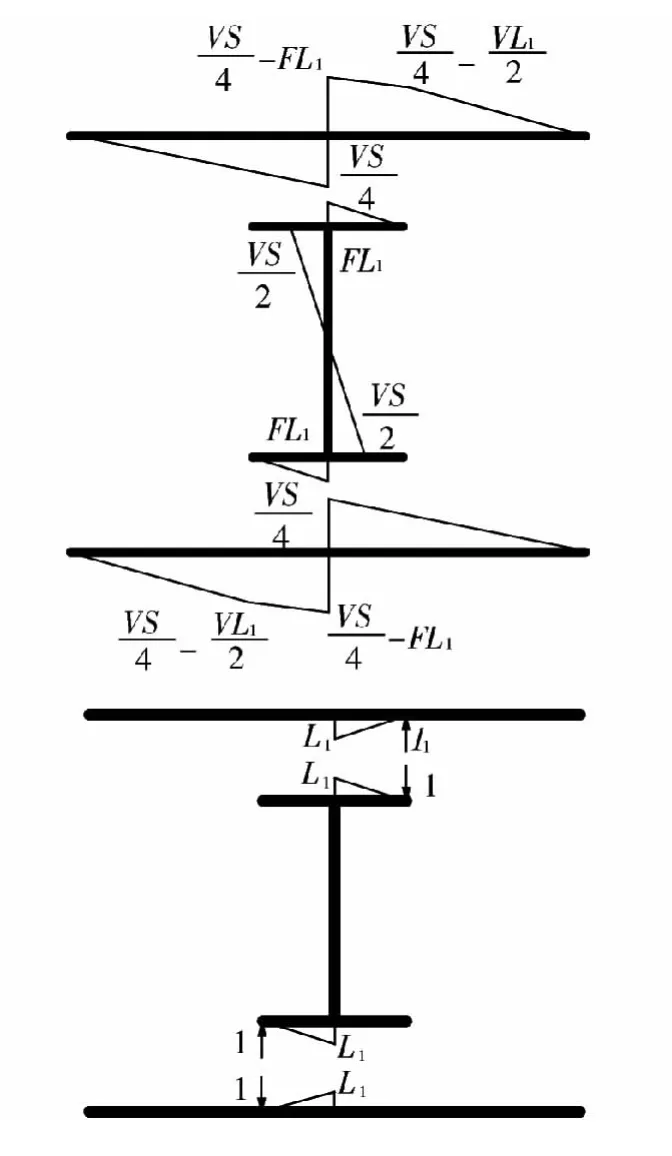
图6 单元弯矩图Fig.6 Bending moment diagram of typical segment

欲求表层板左右端部相对位移,由位移法可知,可在上下表层板左侧加方向竖直向上的单位力,在上下表层板右侧加方向竖直向下的单位力,则表层板与翼缘端部的接触应力变为,单元受力如图7所示。


图7 单元弯矩图Fig.7 Bending moment diagram of typical segment
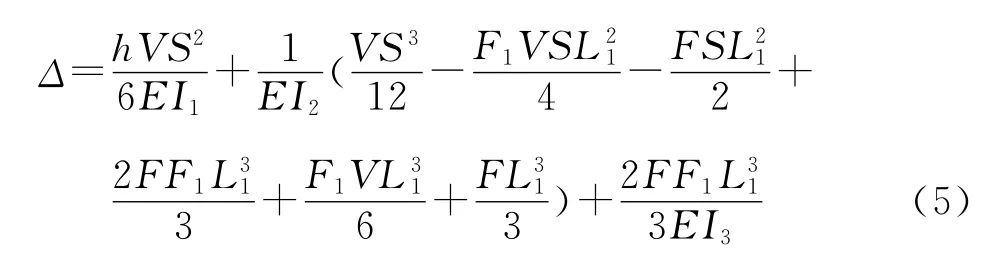
其中,L1为L/2;I1为工字型钢翼缘惯性矩;I2为工字型钢腹板惯性矩;I3为夹层板惯性矩。以上公式推导中的E基于梁理论;而实际所需的E1应该是基于平面应力理论,所以这里应该将E转化为E1;且上面推倒的公式是上下表层板左右端相对位移之和,所以单元实际挠度计算公式应为其1/2,得工字型夹层板弱方向挠度计算公式:
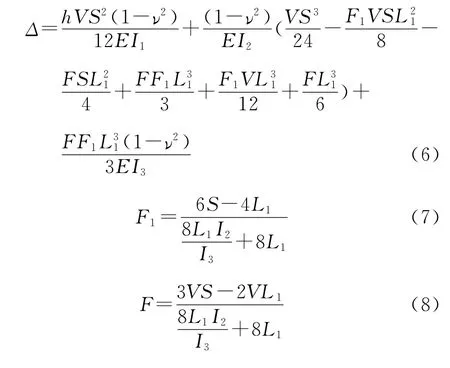
2 实例分析
通过Abaqus建立八跨工字型夹芯简支梁有限元模型,其中每个模型的表层板厚度t1,工字型钢翼缘厚度为t2,翼缘长度为L=2L1,工字型钢腹板厚度为t3,腹板的高度为h,相邻工字型钢之间的间距为S,所用材料为同种钢材,弹性模量E=206 000MPa,泊松比v=0.3,在夹层板弱方向1/2长度处作用集中力7.5N。
为了探究公式(6)的适用范围,取对计算值与有限元模拟值之间误差有影响的参数进行分析,这些参数包括工字型钢的腹板与翼缘板的比值t3/t2,上表层板与工字型钢的腹板的比值t1/t3,工字型钢翼缘宽度与腹板高度的比值L/h,夹芯间距与腹板高度的比值的比值S/h。
2.1 t3/t2 的变化对误差的影响
建立 A1,B1,C1,D1,E1,F1,G1,H1,I19个模型进行验算分析,模型尺寸如表1所示。

表1 夹层板模型尺寸Table 1 Dimensions of I-core sandwich panel mm
将已知量代入推导公式得计算值,通过Abaqus软件建模得有限元模拟值,并计算两者误差,可得图8~图9。

图8 计算值与有限元模拟值误差比较Fig.8 Comparison of the error between the theoretical and FE results

图9 计算值与有限元模拟值挠度比较Fig.9 Comparison of the deflection of the theoretical and FE results
分析可知:在一定程度上,大约t3/t2<1.5时,工字型钢腹板的厚度t3与工字型钢翼缘的厚度t2的比值越大,推导公式所得计算值和Abaqus软件建模所得有限元模拟值之间的误差越小;当大约t3/t2>1.5时,计算值与有限元模拟值之间误差随着t3/t2的变大而变大,可以看出在t3/t2=1.5附近,计算值与有限元模拟值有较高吻合度,推导公式的精确度较高。在如表1给定尺寸下,当1.25<t3/t2<2.0时,计算值与有限元模拟值的误差在5%以内,不妨初步定1.25<t3/t2<2.0为推导公式的适用范围。当然公式是否在此范围内适用还受其他变量取值的影响,需进一步研究。
2.2 t1/t3 的变化对误差的影响
取 A2,B2,C2,D2,E2,F2,G28个模型进行验算分析,模型尺寸如表2所示。

表2 夹层板模型尺寸Table 2 Dimensions of I-core sandwich panel mm
将已知量带入推导公式得计算值,通过Abaqus软件建模得有限元模拟值,并计算两者误差,可得图10~图11。
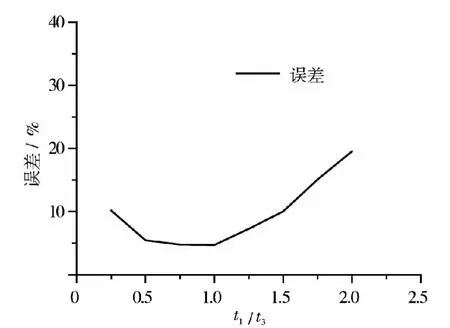
图10 计算值与有限元模拟值误差比较Fig.10 Comparison of the error between the theoretical and FE results

图11 计算值与有限元模拟值的挠度比较Fig.11 Comparison of the deflection of the theoretical and FE results
分析可知:当t1/t3<1时,计算值与有限元模拟值的误差有减小的趋势,当t1/t3>1时,计算值与有限元模拟值的误差有增大的趋势,即在t1/t3=1附近,计算值与有限元模拟值有较好的吻合度,精确度相对较高。
在上述研究t3/t2的变化对计算值与有限元模拟值的误差的影响时得出:当1.25<t3/t2<2.0,公式有较好的精度。在这里可进一步验证:令t1和t3与表2保持一致,令t2逐渐变大,即改变t3/t2的比值,具体尺寸数据如表3。

表3 桁架夹层板模型尺寸Table 3 Dimensions of I-core sandwich panel mm
将已知量代入推导公式得计算值,通过Abaqus软件建模得有限元值,并计算两者误差,可得图12~图13。
将图12和图10相比可以发现,在t1/t3的数值相同时,当t3/t2在1.25<t3/t2<2.0范围内,图12中的误差小于图10的误差,可进一步证明在1.25<t3/t2<2.0范围内,公式具有较高的准确性,不妨在1.25<t3/t2<2.0范围内随机抽取一个数,令t3/t2=1.33,在这个前提下研究t1/t3的变化对计算值与有限元模拟值之间误差影响。

图12 计算值与有限元模拟值的误差比较Fig.12 Comparison of the error between the theoretical and FE results

图13 计算值与有限元模拟值的挠度比较Fig.13 Comparison of the deflection of the theoretical and FE results
取 A4,B4,C4,D4,E4,F4,G4,H48个模型进行验算分析。令t3=2.0,t2=1.5,表层板厚度t1变化进行研究,见表4。

表4 夹层板模型尺寸Table 4 Dimensions of I-core sandwich panel mm
将已知量代入推导公式得计算值,通过Abaqus软件建模得有限元模拟值,并计算两者误差,可得图14~图15。

图14 计算值与有限元模拟值的误差比较Fig.14 Comparison of the error between the theoretical and FE results

图15 计算值与有限元模拟值的挠度比较Fig.15 Comparison of the deflection of the theoretical and FE results
分析可知:在一定程度上,大约t1/t3<1.0时,表层板的厚度t1与工字型钢腹板的厚度t3的比值越大,计算值和有限元模拟值之间的误差越小;当大约t1/t3>1.0时,计算值与有限元模拟值之间误差随着t1/t3的变大而变大,可以看出在t1/t3=1.0附近推导公式的精确度最高。这个结论与模型2中所得结论一致,可进一步证明上述规律的正确性。从整体来看,当t3/t2=1.33时,在0.67<t1/t3<1.67范围内,计算值与有限元模拟值的误差在5%以内,推导公式所得计算值与有限元模拟值有较高吻合度,不妨定1.25<t3/t2<2.0,0.67<t1/t3<1.67为推导公式的适用范围,当然公式是否适用还与其他变量有关,仍需进一步讨论。
2.3 L/h的变化对计算值与有限元模拟值之间误差的影响
取 A5,B5,C5,D5,E5,F5,G5,H5,I59个模型进行验算分析。已经分析得出:在1.25<t3/t2<2.0,0.67<t1/t3<1.67范围内推导公式结果精确度较高。不妨令t3=2.0,t2=1.5,t1=1.5保持不变,工字型钢翼缘长度L变化进行研究,见表5。

表5 桁架夹层板模型尺寸Table 5 Dimensions of I-Core Sandwich panel mm
将已知量代入推导公式得计算值,通过Abaqus软件建模得有限元值,并计算两者误差,可得图16~图17。
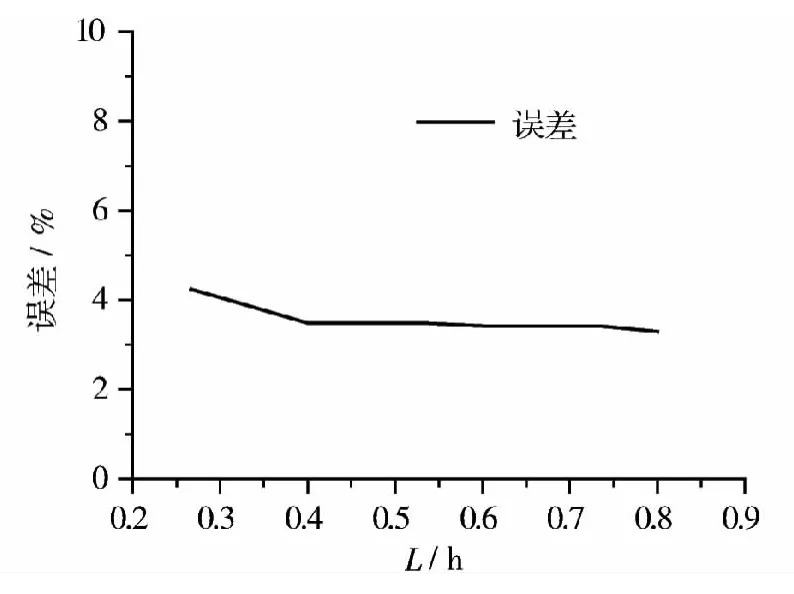
图16 计算值与有限元模拟值的误差比较Fig.16 Comparison of the error between the theoretical and FE results
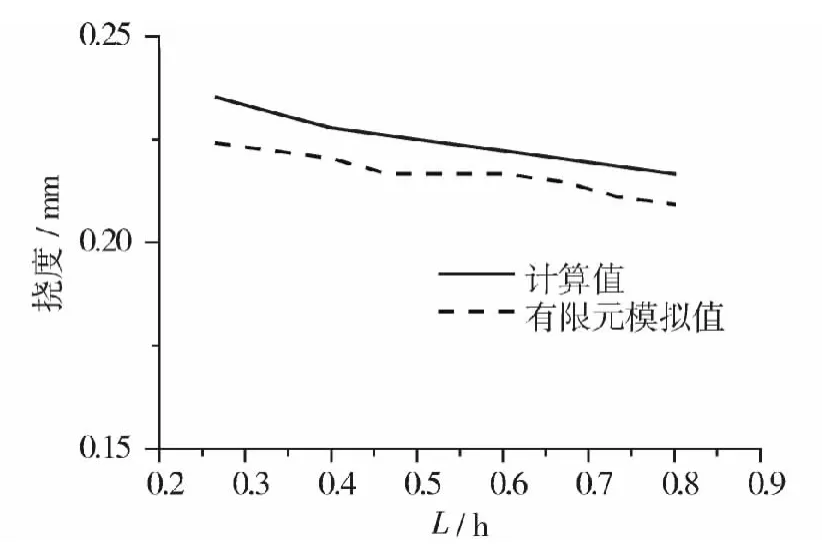
图17 计算值与有限元模拟值的挠度比较Fig.17 Comparison of the deflection of the theoretical and FE results
分析可知:在所研究范围内,计算值与Abaqus软件建模所得有限元模拟值的误差都在5%以内,推导公式所得计算值与有限元模拟值有较高吻合度,公式适用,从整体看,随着L/h增大,误差有减小的趋势。
2.4 S/h的变化对计算值与有限元模拟值之间误差的影响
取 A6,B6,C6,D6,E6,F6,G6,H68个模型进行验算分析。已经分析得出:在1.25<t3/t2<2.0,0.67<t1/t3<1.67内推导公式结果精确度较高。不妨令t3=2.0mm,t2=1.5mm,t1=1.5mm,L=40mm保持不变,工字型钢翼缘长度S变化进行研究,见表6。

表6 桁架夹层板模型尺寸Table 6 Dimensions of I-core sandwich panel mm
将已知量代入推导公式得计算值,通过Abaqus软件建模得有限元值,并计算两者误差,可得图18~图19。
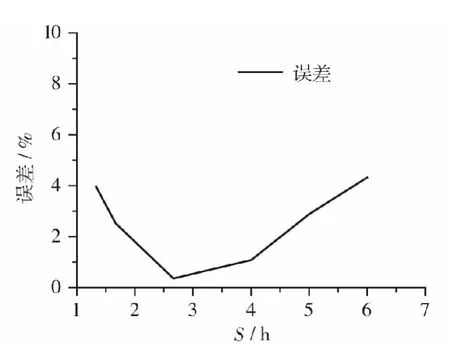
图18 计算值与有限元模拟值的误差比较Fig.18 Comparison of the error between the theoretical and FE results
分析可知:在所研究范围内,计算值与Abaqus软件建模所得有限元模拟值的误差都在5%以内,推导公式所得计算值与有限元模拟值有较高吻合度,公式适用。

图19 计算值与有限元模拟值的挠度比较Fig.19 Comparison of the deflection of the theoretical and FE results
3 结论
(1)工字钢的翼缘宽度与高度的变化对夹层板受跨中集中荷载作用在弱方向的挠度的变化的影响不大。
(2)在t3/t2<1,t1/t3<1时,夹层板受跨中集中荷载作用在弱方向的挠度变化较大。
(3)在25<t3/t2<2.0,0.7<t1/t3<1.6,0.3<L/h<0.8,1.4<S/h<6时,计算值与有限元模拟值有较高的吻合度,公式的准确度较高,定为该公式的适用范围。
[1]王洪欣,查晓雄,余敏,等.爆炸作用下金属面夹层板力学性能研究[J].建筑结构学报,2013,34:401-406.
WANG Hongxin,CHA Xiaoxiong,YU Min,et al.Mechanical behavior of metallic sandwich panels under blast action[J].Journal of Building Structures,2013,34:401-406.
[2]Nordstrand T M.Parametric study of the post-buckling strength of structural core sandwich panels[J].Composite Struct,1995,30:441-451.
[3]Lok T S,Cheng Q H,Heng L.Equivalent stiffness parameters of truss-core sandwich panel[J].Int Offshore Polar Eng Conf,1999,4:292-298.
[4]Lok T S,Cheng Q H.Elastic stiffness properties and behavior of truss-core sandwich panel[J].Struct Eng,2000,126(5):52-559.
[5]王海忠,何保康.建筑夹层板结构性能分析[J].钢结构,1999,14(46):41-45.
WANG Haizhong,HE Baokang.Structural behavior analysis of architectural sandwich panels[J].Steel Construction,1999,14(46):41-45.
[6]Fung T C,Tan K H,Lok T S.Elastic constants for z-core sandwich panels[J].Struct Eng,1994,120(10):3046-3055.
[7]Xu X F,Qiao P Z.Homogenized elastic properties of a honeycomb sandwich with skin effect[J].Int J Solids Struct,2002,39(8):2153-2188.
[8]Deshpande V S,Fleck N A.Isotropic constitutive models for metallic foams[J].Mech Phys Solids,2000,48(6-7):1253-1283.
[9]Xue Z Y,Hutchinson J W.Constitutive model for quasistatic deformation of metallic sandwich cores[J].Int J Numer Methods Eng,2004,61(13):2205-2238.
[10]赵彤,朱礼敏,陈兵,等.预应力混凝土夹层板抗弯性能的试验研究[J].建筑科学,2003,19(5):5-9
ZHAO Tong,ZHU Limin,CHEN Bing,et al Experimental study on flexural behavior of precast concrete sandwich panels[J].Building Science,2003,19(5):5-9.
[11]李华东,朱锡,梅志远,等.静水压力作用下夹层板结构的变形规律分析[J].华中科技大学学报,2010,38(11):119-126.
LI Huadong,ZHU Xi,MEI Zhiyuan,et al.Analyzing the deformation of sandwich plate structure under hydrostatic pressure[J].Journal of Huazhong U-niversity of Science and Techndogy,2010,38(11):119-126.
[12]潘鹏,钱稼茹,潘振华,等.钢丝网架水泥细石夹层板水平承载力试验研究及简化计算方法[J].建筑结构,2010,40(4):41-43.
PAN Peng,QIAN Jiaru,PAN Zhenhua,et al.Experimental study and simplified calculation method of prefabricated steel-mesh cement infilled panels[J].Building Structure,2010,40(4):41-43.
[13]查晓雄,宋新武.建筑用绝热金属面夹层板抗弯承载力的统一理论和有限元分析[J].工业建筑,2011,41(3):16-22.
CHA Xiaoxiong,SONG Xinwu.Study on the bending capacity of metal surface insulating sandwich panels by unified theory and FE analysis[J].Industrial Construction,2011,41(3):16-22.
[14]WANG Yamin,SHAO Yongbo,LIU Yukai.Prediction on deflection of truss-core sandwich panels in weak direction[J].The Open Ocean Engineering Journal,2013,6:65-72.
