独塔斜拉桥抗震分析及其合理约束体系研究＊

姜冲虎，杨博闻，李德建，杨孟刚

（1.中南大学 土木工程学院，湖南 长沙410075；2.长沙理工大学 华罡规划设计研究院，湖南 长沙410004；3.长沙理工大学 土木与建筑学院，湖南 长沙410004）

独塔斜拉桥以其造型美观、跨越能力较强而越来越多地被采用，尤其是在跨越铁路、公路时因其梁体轻盈而有着独特的优势。近年来，随着人们对抗震设计的进一步重视，独塔斜拉桥的抗震性能以及合理的约束体系也受到人们越来越多的关注。

斜拉桥常用的结构体系包括：漂浮体系（塔梁分离）、支承体系（塔梁间设置支座或其他支承）、刚构体系（塔、梁、墩固结）等。一般而言，对于独塔斜拉桥，选用刚构体系是较为适宜的［1］。但在地震高烈度地区，由于刚构体系刚度大，自振周期小，地震响应强烈，往往导致桥塔底部产生较大的内力。此时，为了满足抗震受力要求，往往需要增大桥塔截面尺寸和配筋，而这样一来使得结构的刚度和自重进一步增大，地震响应更为强烈，从而陷入恶性循环，既不经济也不合理。因此，有必要寻求更为合适的约束体系，使独塔斜拉桥在满足正常使用荷载的前提下能更好地适应地震作用，改善结构的抗震性能。本文以石河子斜拉桥为工程背景，通过计算其在不同约束条件下的纵向地震响应，寻求最优的纵向约束体系。

1 工程背景简介

石河子斜拉桥是石河子市西一路高架桥的主桥部分，位于石河子市南侧，上跨北疆铁路，与铁路的夹角约76°，桥跨布置为2×90m独塔斜拉桥，桥梁全长179.84m。全桥采用塔、梁、墩固结的刚构体系，桥塔采用钢筋混凝土花瓶形桥塔，主梁采用预应力钢筋混凝土“Π”型梁，斜拉索采用空间双索面。桥型布置见图1。

桥位所在区域地震动峰值加速度为0.2g，特征谱反应周期为0.45s。地基土以卵石为主，属抗震有利路段，可不考地震液化问题，工程场地类别为Ⅱ类［2］。

图1 桥型总体布置图Fig.1 Overall bridge bridge－type layout

2 抗震计算模型及方法

独塔斜拉桥纵向抗震分析可采用传统的简化模型，如图2所示。简化模型将主塔的质量换算成等效质量集中于塔顶，图中，F1为主塔惯性力，F2为主梁惯性力，M2为主梁质量［3］。

随着计算机技术和结构分析软件的飞速发展，目前多采用有限元方法，即按实际情况建立结构的有限元计算模型进行计算分析，可得到更为精确的结果。

对于本桥，利用大型通用软件 Midas建立有限元模型，将全桥离散为452个梁单元，建模时考虑过渡墩但不考虑引桥的影响。采用m法模拟桩土联合作用，利用主从关系模拟支座约束。有限元计算模型见图3［4－5］。

图2 纵桥向简化模型图Fig.2 Longitudinal simple calculation model

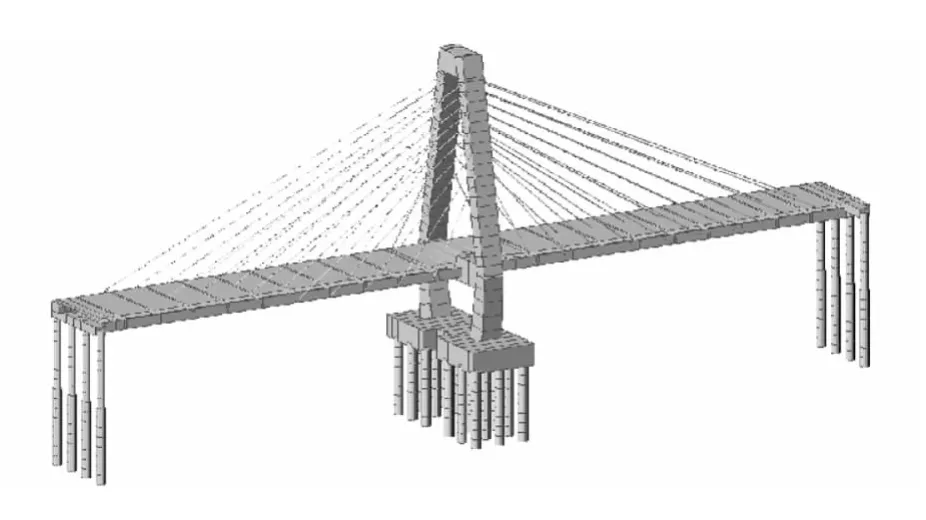
图3 有限元计算模型图Fig.3 FEA model

现有的常用地震分析方法有静力法、反应谱法、动力时程分析方法和功率谱法等［6］。

对于本桥，首先采用反应谱法进行初步的地震分析，得到控制性的结果，然后采用动力时程法进行分析，可得到更为精细的结果以及全过程的地震响应［7－8］。

3 独塔斜拉桥抗震分析

3.1 反应谱分析

按《公路桥梁抗震设计细则》JTG／T B02－01－2008（以下简称08细则）的要求计算E2地震作用下的水平设计加速度反应谱，分析时采用多自由度振型叠加法，振型数量选择100阶，保证各方向均获得90%以上的有效质量，振型组合采用CQC法，阻尼系数取为0.05。运行反应谱分析，可得本桥的基本振型为主梁纵向挠曲，基本周期为1.503s。在顺桥向反应谱作用下，结构的主要计算结果如表1所示。

表1 顺桥向E2反应谱分析计算结果Table 1 Results of transversal E2response spectrum analysis

3.2 动力时程分析

采用动力时程分析法时选用合适的地震波输入是计算的关键，采用不同的地震输入，得到的结果差别极大。本文采用三角级数法，生成了3条E2人工地震波，见图5所示。该法利用快速傅里叶变换技术，生成拟合反应谱的人工地震波，不仅能满足地震波3要素，而且与现行的反应谱法相衔接［5－6］。

针对3条地震波分别运行时程分析，计算时采用非线性直接积分法，分析时间取30s，时间步长取0.01s，阻尼采用质量和刚度因子法计算，各阶振型的阻尼比均取为0.05，迭代计算以位移为收敛标准。计算之后，可得到各截面内力、位移的时程曲线，取其绝对值最大者即为该截面控制值。在以上3条人工地震波作用下，结构的主要计算结果见表2。

从表中结果可知，3条人工波的时程分析结果与反应谱分析结果较为接近，其相对偏差均在±20%之内，表明时程分析结果基本可靠，人工地震波的选用基本合适。根据《08细则》的要求，当采用3组时程波计算时，取计算结果的最大值。

图4 水平设计加速度反应谱图ig.4 Response spectrum of horizontal design acceleration

表2 顺桥向E2动力时程分析计算结果Table 2 Results of transversal E2dynamic time－history analysis

4 纵向合理约束体系探讨

斜拉桥常用的结构体系包括：漂浮体系、支承体系和刚构体系等。一般而言，对于独塔斜拉桥，选用刚构体系是较为适宜的，在正常使用荷载作用下，刚构体系的刚度、强度和稳定性等各方面均为最优。但在地震高烈度地区，由于刚构体系刚度大，自振周期小，地震响应强烈，往往导致桥塔底部产生较大的内力［7］。因此，有必要寻求更为合适的约束体系，使独塔斜拉桥在满足正常使用荷载的前提下能更好地适应地震作用，改善结构的抗震性能。

针对刚构、漂浮和支承等各种不同的约束体系，在相同的地震作用下分别进行抗震分析，对其结果进行比较，以寻求合理的约束体系。

4.1 刚构体系

刚构体系塔、梁、墩3者固结，体系刚度大，在正常荷载及风振、车振作用下结构稳定性好，承载力强，是独塔斜拉桥中最为常见的约束体系。梁体及桥面荷载大部分通过塔梁固结传递给桥塔，一部分通过拉索传递到上塔柱。在地震作用下，由于刚构体系刚度大，自振周期小，地震响应强烈，在塔底会产生较大的弯矩及剪力，但塔顶及梁体位移较小。如上文所述，在刚构体系下桥梁的一阶振型为主梁纵向挠曲，相应周期为1.503s。

4.2 漂浮体系

漂浮体系塔梁分离，体系刚度小，结构稳定性和承载能力相对较差；加之梁体及桥面荷载全部由斜拉索承担，导致斜拉索（尤其是靠近桥塔的短索）索力过大，故在独塔斜拉桥中一般较少采用。在地震作用下，由于漂浮体系刚度小，自振周期大，在塔底产生的内力相对较小，但是塔顶及梁体位移较大。对于本桥，在漂浮体系下桥梁的一阶振型为主梁纵向挠曲＋漂移，相应周期为3.779s。

4.3 支承体系

在塔梁之间设置支承，一般是设置纵向自由的活动支座，称之为支承体系，或半漂浮体系。由于竖向支承的存在，使得梁体及桥面荷载的一部分可以通过其传递给桥塔，其余部分通过拉索传递。在自重作用下，拉索的传力比例与刚构体系基本相同。对于本桥，在支承体系下桥梁的一阶振型及周期与漂浮体系相同。

当采用纵向自由的活动支座做为竖向支承时，是否考虑支座摩阻力是影响抗震计算的一个重要因素。不考虑支座摩阻力是偏于安全的，但可能会使结果过于保守，造成不必要的浪费。考虑支座摩阻时，活动支座可等效为弹性索和阻尼器的并联，在程序中可采用滞后系统进行模拟［9－10］。滞后系统的恢复力模型见图5。

图中，k为弹性刚度，可近似取为k＝Fy／0.002；Fy为屈服强度，对于活动支座为滑动摩阻力，Fy＝恒载反力N×摩阻系数μ；r为屈服后强度与屈服前强度之比，r＝0。对于本桥，主塔处单个支座的摩阻力为146kN，弹性刚度k＝74 475 kN／m；过渡墩处单个支座的摩阻力为72.9kN，弹性刚度k＝36 465kN／m。

图5 滞后系统恢复力模型图ig.5 Mechanical model for time－delay system restoration

对考虑与不考虑摩阻力的情况分别进行了计算，结果见表3。

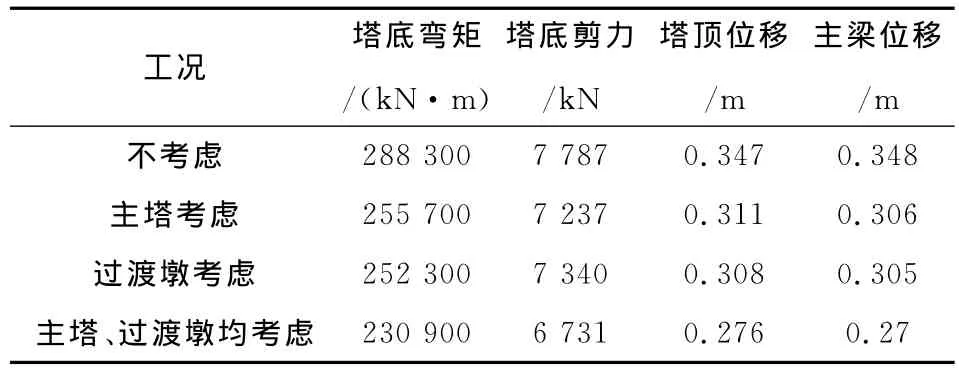
表3 支座摩阻力对抗震的影响计算结果Table 3 Bearing resistance influencing in seismic reduction

从表中结果可知，考虑支座摩阻力对抗震计算结果有很大的改善，塔底内力及塔顶、主梁位移均有较大的降低，故在采用支承系统时应考虑支座摩阻力。下文的计算结果均为考虑支座摩阻力后的计算结果。

4.4 铰接体系

为了控制塔、梁位移，塔梁之间在竖向支承之外再设置纵向约束，即成为铰接体系。铰接体系与刚构体系的不同之处在于刚构体系在塔梁间可传递弯矩，而铰接体系不传递弯矩。因此，在地震作用下，铰接体系下的塔底弯矩可能会大于刚构体系。同时，结构的振型也可能发生变化。对于本桥，在铰接体系下塔底的弯矩略大于刚构体系，剪力则略小于刚构体系；塔顶及主梁的位移与刚构体系相差不大；结构的一阶振型变为主梁、过渡墩横向挠曲，相应周期为1.946s。

4.5 支承加弹性索体系

从前文可知，独塔斜拉桥的常规约束体系在抗震性能上都有一定的缺陷：刚构及铰接体系结构位移小，但塔底内力过大；漂浮及支承体系塔底内力较小，但塔顶及主梁位移过大。合理的约束体系应使结构的内力、位移2方面均得到有效的控制，因此，人们在支承体系的基础上，在塔、梁之间设置减隔震设施，从而形成新的约束体系，弹性索是其中常见的一种［8］。

塔梁之间采用弹性索连接，可以有效地减小塔、梁的位移，也可以将一部分水平力通过弹性索传递给桥塔，减小了拉索的受力并降低了水平力的传力高度［5］。但同时，由于弹性索增大了结构体系的刚度，随着弹性索刚度K的增加，体系的振动周期甚至基本振型都可能发生变化，因此，K的取值是此体系的关键。显然，当K趋于0时，即为支承体系；当K趋于无穷大时，即为铰接体系。对本桥，取K在10 000～100 000kN／m 的范围内分别进行计算，以寻求最佳的参数取值，同时观察塔底弯矩、剪力、塔顶位移、主梁位移等关键结果的变化规律，见图6～图8。

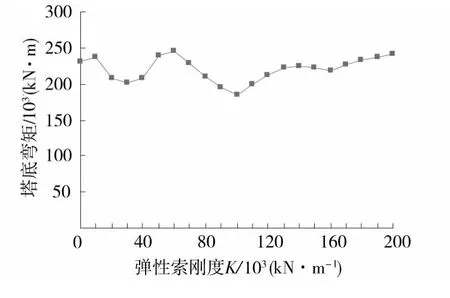
图6 弹性索体系塔底弯矩图Fig.6 Bending moment at the bottom of elastic－cable system

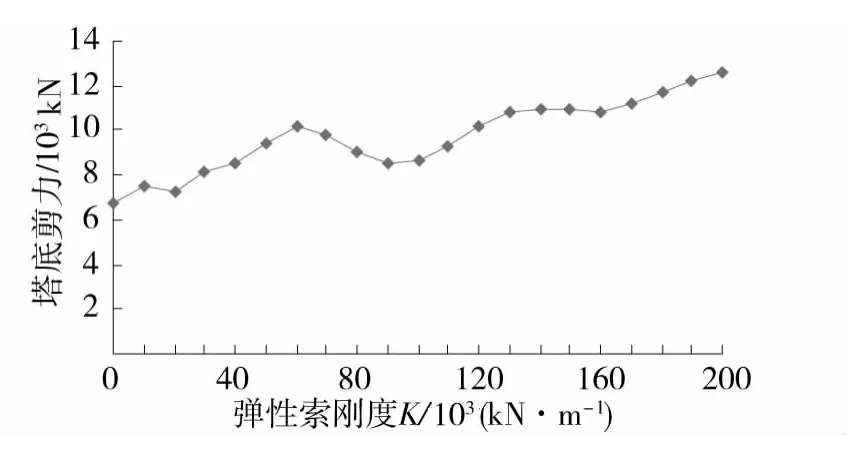
图7 弹性索体系塔底剪力图Fig.7 Shear force at the bottom of elastic－cable system

从图中结果可知，随着弹性索刚度K的增加，塔底弯矩大体上呈一个先增大后减小再增大的过程。塔底剪力的情况与弯矩基本类似，需要注意的是，当K值在某些范围内时，弹性索体系的塔底弯矩比支承体系要小；而对于塔底剪力，无论K取何值，弹性索体系的值都要比支承体系大。因此，对于塔底剪力，采用弹性索体系是不利的。

图8 弹性索体系塔顶及主梁位移图Fig.8 Pylon－top and beam displacement in elastic－cable system

对于塔顶及主梁位移，采用弹性索体系效果是较为明显的。随着K的增大，塔顶及主梁位移总体上呈下降趋势，其中，主梁位移的变化过程较为单一，而塔顶位移则随着K增大有一些起伏波动。在K达到150 000kN／m即基本振型发生变化之后，位移的变化趋势变缓。

综上所述，弹性索体系对于控制塔底内力效果不明显，甚至是不利的；对于控制位移较为有效。由于体系的周期随着弹性索刚度的变化而变化，故采用弹性索体系时内力、位移的变化规律不明显，必须通过计算确定合适的弹性索刚度取值。

4.6 支承加阻尼器体系

合理的约束体系应该使结构在内力、位移两方面均得到适当的控制，从而提高抗震性能。为此，阻尼器以其优良的滞回耗能性能，在越来越多的抗震设计中被应用，其中，在桥梁工程中应用最为广泛的是液体黏滞阻尼器（FVD）。液体黏滞阻尼器通过活塞与容器间的相对运动提供阻尼力，达到减震耗能的目的。黏滞阻尼器没有起始刚度，对于温度变化、收缩徐变等因素引起的梁体慢速变形不产生附加内力，而对于地震动产生的结构快速变形，却能迅速耗能，并且能减小结构的加速度和位移［11－12］。

对于独塔斜拉桥，在塔梁交接处或过渡墩处设置黏滞阻尼器与活动支座配合使用，可以进一步改善结构的抗震性能，使得塔底内力及桥塔、主梁的位移均得到有效的控制。由于黏滞阻尼器没有初始刚度，因此，当阻尼器型号变化时，结构的振动周期和振型不发生变化，内力和位移的变化规律性较为明显。具体的阻尼器型号及布置方式应通过计算来确定。

4.7 体系比选

各约束体系下各控制截面的内力、位移如表4所示。

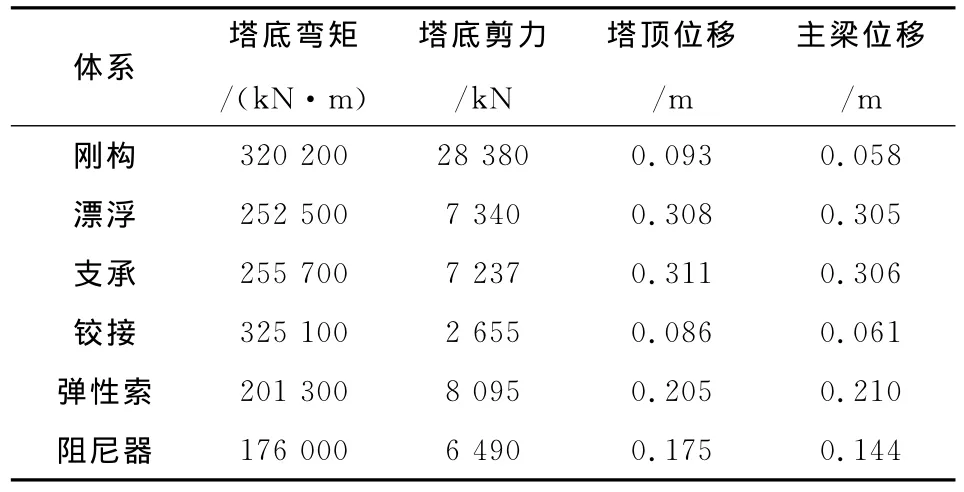
表4 各约束体系纵向抗震计算结果对比Tabel 4 Comparison between calculation results for longitudinal seismic in various restraint

根据08细要求，E2地震作用下，主塔等重要结构受力构件局部可发生可修复的损伤，但要求地震后基本不影响车辆通行，即桥塔截面的弯矩应小于等效抗弯屈服弯矩Meq；同时，主梁位移应满足支座位移量的要求。对于本桥，塔底截面为5（横向）×4.5（纵向）的矩形截面，对其进行M－φ分析，可得到Meq约为343 834kN·m；主塔处设支座时，可采用2个GPZ（II）10活动支座，位移量为±0.25m。

从表4的计算结果可看到，漂浮、支承体系主梁位移过大，不满足要求；刚构、铰接体系塔底弯矩虽可满足要求，但已接近限值，安全富余不大，同时由于抗震成为了结构设计的控制性因素，造成截面尺寸和结构配筋都偏大，导致一定的浪费；弹性索和阻尼器体系塔底弯矩和主梁位移均满足要求，其中，阻尼器体系显然效果更好。采用阻尼器体系时，塔底弯矩较之刚构体系降低了45%。仅从抗震方面考虑，若采用相同的配筋量，塔底截面尺寸可优化为3.5（横向）×3（纵向）（此时的为Meq约为202 590kN·m），大大节省材料。

通过以上比选，可以认为，对于两跨对称的独塔斜拉桥，支承＋阻尼器体系是相对最优的纵向抗震约束体系。

5 结 论

（1）对于独塔斜拉桥，建议采用反应谱法和动力时程法2种方法进行抗震分析，可将反应谱法计算结果作为控制值，并可作为动力时程法选波是否合适的评判标准之一。对于动力时程法，地震波的选取是计算的关键因素，三角级数人工合成法是广泛应用的适用的方法。

（2）当采用纵向自由的活动支座作为竖向支承时，支座摩阻力对结构的抗震性能有较大的提升，计算时应考虑其作用。

（3）在独塔斜拉桥的各种结构体系中，刚构及铰接体系结构位移小，但塔底内力过大；漂浮及支承体系塔底内力较小，但塔顶及主梁位移过大；弹性索体系对于控制位移较为有效，但对于控制塔底内力效果不明显，甚至是不利的，同时体系的内力、位移的变化规律不明显；阻尼器体系对于控制塔底内力及结构位移均有较好的效果，是相对最为理想的纵向抗震体系。

［1］JTG／T D65－01－2007，公路斜拉桥设计细则［S］.JTG／T D65－01－2007，Guidelines for design of highway cable－stayed bridge［S］.

［2］JTG／T B02－01－2008，公路桥梁抗震设计细则［S］.JTG／T B02－01－2008，Guidelines for seismic design of highway bridges［S］.

［3］黄小国，李建中，郭磊.地震作用下独塔斜拉桥合理约束体系［J］.结构工程师，2008，24（6）：29－35.

HUANG Xiaoguo，LI Jianzhong，GUO Lei.Appropriate constraint systems for simple－tower cablestayed bridges under earthquake［J］.Structural Engineers，2008，24（6）：29－35.

［4］刘昊苏，董军，杨昀.不同设计参数下矮塔斜拉桥的抗震动力学分析［J］.工程力学，2013，30（增1）：137－141.

LIU Haosu，DONG Jun，YANG Yun.Seismic response for an extradosed cable－stayed curved bridge with different design parameters［J］.Engineering Mechanics，2013，30（Supp1）：137－141.

［5］焦常科，李爱群，伍小平.大跨双层斜拉桥地震响应控制［J］.应用基础与工程科学学报，2012，20（4）：704－712.

JIAO Changke，LI Aiqun，WU Xiaoping.Seismic response control of double－deck long－span cablestayed bridges［J］.Journal of Basic Science and Engineering，2012，20（4）：704－712.

［6］胡聿贤.地震工程学［M］.2版.北京：地震出版社，2006：150－173.

HU Yuxian.Introduction to earthquake engineering［M］.2nd ed.Beijing：Earthquake Publishing House，2006：150－173.

［7］Camara A，Astiz M A.Pushover analysis for the seismic response prediction of cable－stayed bridges under multi－directional excitation［J］.Engineering Structures，2012（41）：444－455.

［8］Ahmet Can Altunis－ik，Alemdar Bayraktar，Baris Sevim，et al.Ambient vibration based seismic evalua－tion of isolated gulburnu highway bridge［J］.Soil Dynamics and Earthquake Engineering，2011（31）：1496－1510.

［9］Shahria Alam M，Rahman Bhuiyan M A，Muntasir Billah A H M.Seismic fragility assessment of SMA－bar restrained multi－span continuous highway bridge isolated by different laminated rubber bearings in medium to strong seismic risk zones［J］.Bull Earthquake Eng，2012（10）：1885－1909.

［10］Rahman Bhuiyan A，Shahria Alam M.Seismic performance assessment of highway bridges equipped with superelastic shape memory alloy－based laminated rubber isolation bearing［J］.Engineering Structures，2013（49）：396－407.

［11］姜冲虎，李德建.大跨度连续梁桥SSAB与FVD组合应用减隔震技术研究［J］.铁道科学与工程学报，2013，10（6）：28－32.

JIANG Chonghu，LI Dejian.Seismic isolation technology research of long－span continuous beam bridge with SSAB and FVD［J］.Journal of Railway Science and Engineering，2013，10（6）：28－32.

［12］聂利英，李建中，胡世德.任意荷载作用下液体粘滞阻尼器在桥梁工程中减震作用探讨［J］.计算力学学报，2007，24（2）：197－202.

NIE Liying，LI Jianzhong，HU Shide.Investigation of decreasing vibration effects of fluid viscous damper in engineering under random loads［J］.Chinese Journal of Computational Mechanics，2007，24（2）：197－202.