基于矩阵的Apriori改进算法与实现

张小林

关联规则[1-4]由Agrawal、Imielinski和Swami于1993年在对市场购物篮问题进行分析时首次提出，用以发现商品销售中的顾客购买模式，是数据中一种简单但很实用的规则。关联规则的主要思想就是找出频繁项集，算法的主要工作就是寻找K-项集。根据相关性质，频繁项集的子集必是频繁项集，非频繁项集的超集一定是非频繁的。利用上一步产生的频繁项集来生成长度更大的项集，并将其称之为候选频繁项集。候选频繁项集是指那些有可能成为频繁项集的集合。算法先计算所有的候选1-项集C1；从C1中找出所有的频繁1-项集L1；然后，再将L1与自身做连接运算，生成候选2-项集的集合C2；从C2中找出所有的频繁2-项集L2；再将L2与自身做连接运算，生成候选3-项集的集合C3；从C3中找出所有的频繁3-项集L3；如此下去直到不再产生新的候选集。一般地，将候选K-项集的集合记为Ck，将频繁k-项集记为Lk，显然Lk哿Ck。

1 关联规则的算法简介

挖掘关联规则的一种原始方法：计算每个可能规则的支持度和置信度。这种方法的过高代价令人望而却步，因为可以从数据集提取的规则的数目达指数级。具体点说，从包含d个项的数据集提取的可能规则的总数为：R=3d-2d+1+1。

提高关联规则挖掘算法性能的第一步是拆分支持度和置信度要求。因此，大多数关联规则挖掘算法通常采用的一种策略是，将关联规则挖掘任务分解为如下两个主要的子任务：(1)频繁项集产生。其目标是发现满足最小支持度阈值的所有项集找出所有的频繁项集。(2)规则的产生。其目标是从上一步发现的频繁项集中提取高置信度的规则。这两个步骤中，第二步是在第一步的基础上进行的，工作量非常小。挖掘关联规则的总体性能由第一步决定。

关联规则的挖掘有很多方法，比较典型的算法有两种：

(1)ARGen算法。ARGen算法由Agrawal和Ramakrishman提出的，过程如下：

(2)Apriori算法

Apriori算法在关联规则算法分析中具有相当重要的地位，其中含有priori是因为算法使用了频繁项集性质的先验（priori）知识。Apriori算法是由Agrawal等在1993年提出的，主要是基于数据库中数据项之间的关联规则。随着需求的不断扩大，应用范围的拓展，随后几年有很多的理论研究人员开始对Apriori算法感兴趣。因此，Apriori算法一直被称为经典算法，后来的一些算法主要是对经典算法进行优化，被称之为类Apriori算法。

2 Apriori算法的核心思想

Apriori算法的核心思想主要如下：

(1)通过单趟扫描事务数据库D计算出所有1-项集的支持度，从而得到满足最小支持度s%的频繁1-项集构成的集合L1。

(2)为了产生频繁k-项集构成的集合Lk，必须先产生候选频繁k-项集的集合Ck，产生Ck的方法是连接。过程如下所述：设li是Lk-1中的项集，li[j]表示li的第j项。在此假定事务或项集中的项按一定顺序排列。设l1、l2是Lk-1中的项集，如果它们的前（k-2）个项相同，则l1、l2是可连接的，即如果（l1[1]=l2[1]）∧（l1[2]=l2[2]）∧…∧（l1[k-2]=l2[k-2]）∧（l1[k-1]≠ l2[k-1]），则连接l1和l2产生的结果项集是l1[1]l1[2]…l1[k-2]l1[k-1]l2[k-1]。由Lk-1中可连接的项集连接所产生的k-项集的集合便是Ck。

(3)由于Ck是Lk的超集，可能有些元素不是频繁的。由于任何非频繁的（k-1）项集必定形不成频繁k-项集的子集，所以，当候选k-项集的某个（k-1）子集不是Lk-1中的成员时，则该候选频繁项集不可能是频繁的，可以从Ck中移去。通过单趟扫描事务数据库D，计算Ck中各个项集的支持度。将Ck中不满足最小支持度计数s的项集删除，生成频繁k项集Lk。

通过迭代循环，重复上述步骤，直到不能产生新的频繁项集的集合为止。在频繁项集的基础上筛选出支持度大于最小支持度的频繁项集，最终找到满足设定好的最小支持度和最小置信度的频繁项集，产生关联规则。

3 Apriori算法不足与改进思路

Apriori算法的思想是查找频繁项集，尽管它也在产生候选集的时候也采取了一些措施，但是仍然存在一些致命的缺点。

(1)当所挖掘的数据量很大，它可能需要产生大量候选项集。例如，如果有104个频繁1项集，则Apriori算法需要产生多达107个候选2项集，如果还要产生候选3-项集，那所产生的数据量无法估量了，显然效率极低。此外，为发现长度为100的频繁模式，如{a1,…,a100}，必须产生多达2100≈1030个候选。

(2)每当产生一个候选集的时，它就需要重新扫描数据库D，通过模式匹配来计算候选集中每个项集的支持度计数，显然通过扫描事务数据库中每个事务来计算候选项集的支持度的开销非常大，而且事务数据库中的事务数越多，效率越低。

根据以上缺点，很多理论研究者提出了一些改进算法和新的技术[5]，以提高Apriori算法的效率。主要的一些技术如下所述：

(1)基于散列的技术（散列项集到对应的桶中）：散列技术实际上是通过减少候选集的方法来提高算法效率的技术。改进思想是，当有候选1-项集产生频繁1-项集时，在扫描事务数据库的同时，也对它们每个事务可能产生的候选2-项集散列到所定义的散列表数据结构（桶）中，并将对应的桶的计数增加。然后在查找散列表中各个桶的计数，如果小于支持度阈值，那么该2-项集是非频繁的，应该从候选集中删除。该压缩算法对2-项集是非常有用的。

(2)事务压缩（压缩未来迭代扫描的事务数）：根据频繁项集的性质，不包含任何频繁k项集的事务，它不可能包含任何频繁（k+1）项集。算法思想就是利用了上述的性质，如果事务不包含频繁2-项集，那么它就不可能包含频繁3-项集，频繁4-项集。因此在产生频繁项集的时候，不断地发现这些事务，并将这些事务屏蔽，通过加上特殊的标记或者删除，因为这些事务不可能再产生更多的频繁项集，以减少下一步产生频繁项集扫描数据库的次数。

(3)划分（为寻找候选项集划分数据）：使用划分技术，实际上就是将事务数据库从逻辑上划分成n个不相交的划分块，然后再针对每个划分块查找频繁项集，最后将所有的划分块中的频繁项集集合起来，从中找出频繁项集。因此使用划分技术只需要扫描两趟事务数据库，一次是在每个划分块中，另一次是在集成频繁项集的时候。尽管划分技术从理论上来说，是减少了数据库的扫描次数，但是在实际实现过程中，还是存在很多问题，将数据库划分为多少个块，太多太少都不合适，还有就是如果从CPU运行的效率上来说，并行处理效率更高，但是它会受到每个划分产生的频繁项集之间通信的制约。

(4)采样（对给定数据的子集挖掘）：采样技术在很多领域中都在应用，在统计学中的应用更为广泛。现在将它引用到数据挖掘中，主要来解决数据挖掘中数据量大的问题。抽样方法的基本思想和其他应用领域中是一样的，从给定的数据中选取样本，但是所选取的样本要具有代表性。选定样本后，在根据挖掘算法对样本进行查找频繁项集，而不是在给定的原始数据中查找频繁项集，这样大大提高了频繁项集的查找效率。当由样本生成的频繁项集，产生一些规则，然后用非样本数据库的事务去验证哪些规则是成立的。显然，这种方法也有它的一些弊端，肯定会丢失一些频繁项集，遗漏一些重要的规则，毕竟样本不能代表所有的数据。采样技术，可以减少数据库的扫描次数，提高了系统的I/O性能。

4 基于矩阵的挖掘算法

关联规则挖掘主要分为两个步骤，首先是找出所有的频繁项集，然后是通过这些频繁项集产生关联规则。根据开始设置的最小支持度和最小置信度来提取关联规则。

在具体实现的时候，采取了一种新的改进算法。它的主要思想是：(1)减少事务数据库记录数量；(2)尽量减少读取数据库操作。在压缩事务数据库采取的策略是，尽量删除那些不可能得到频繁项集的项目。改进算法思想是，利用矩阵的的数据结构特点，直接查找频繁项集。定义矩阵数据结构，行向量表示项目，列向量表示事务。矩阵X为：

图中I1…Im表示m个项目，T1…Tn表示n个事务。yji(1≤j≤m,1≤i≤n)只能等于0或者1。行向量可以理解为，项目在哪些事务中；列向量可以理解为什么，当前事务包含哪些项目。譬如，当y11=1时，表示项目I1在事务T1中，当y21=0时，表示项目I1不在事务T2中。当yji=1时，表示项目Ij在事务Ti中，反之则不在事务Tj中。此算法只需读取一次数据库，在读取的同时就开始给每个项目计数。

当查找频繁1-项集时，只需计算当前项目Ii的行向量的和，当min_sup时，则Ij是频繁1-项集。将当前项目Ij写入数据库中，并将它的支持度计数同时写入数据中。反之则不是频繁项集，则也要将它写入数据库中，并标上标记，只要当后面出现此项目的时候，就不需要计算了，肯定是不频繁的。

当查找频繁2-项集时，同样是求和。具体算法如下：sum（IjIk）=yj1×yk1+yj2×yk2+…+yjn×ykn，当sum（IjIk）≥min_sup时，IjIk是频繁2-项集，反之就不是频繁2-项集；同上，要将频繁的项集和非频繁的项集写入数据库，为它们分别标上标记，对于非频繁的项集，在下次出现的时候，直接跳过。当查找频繁3-项集时，算法和2-项集一样，求每个项目的列向量的积，然后求和，当求的值大于或等于最小支持度，就是频繁的。

sum（IjIkIp）=yj1×yk1×yp1+yj2×yk2×yp2+…+yjn×ykn×ypm，当Sum（IjIkIp）≥min_sup时，IjIkIp是频繁3-项集，反之就不是频繁3-项集；然后将它们写入数据库，并标上标记。

在上述运算中，由于矩阵具有一些运算法则，可以直接将Ij∧Ik进行与运算，然后统计当前向量的和是否满足最小支持阈值的计数。如此循环，直到不能发现新的频繁项集，算法结束。在查找频繁K-项集时，可以利用到在查找频繁K-1项集时的数据。因为矩阵中的数据yji=0或者yji=1，因此也可以使用与运算来计算。目前，CPU性能相当的高，执行加法运算速度相当快，相对于在Apriori算法中用到的连接运算来说，效率明显提高了。

5 实验结果

将改进后的Apriori算法应用到Apache+PHP+Mysql平台上开发的web日志挖掘系统中。利用改进后的算法对学校的招生就业网站进行分析。从访问web的IIS日志中提取了相关信息进行数据挖掘，主要是希望能挖掘到一些访问信息，对网站的结构布局进行改版，便于不同要求的访客能快捷地找到有用的信息。

在经过数据净化、会话识别等步骤后，得到用户的事务集，如表1所示（部分）。

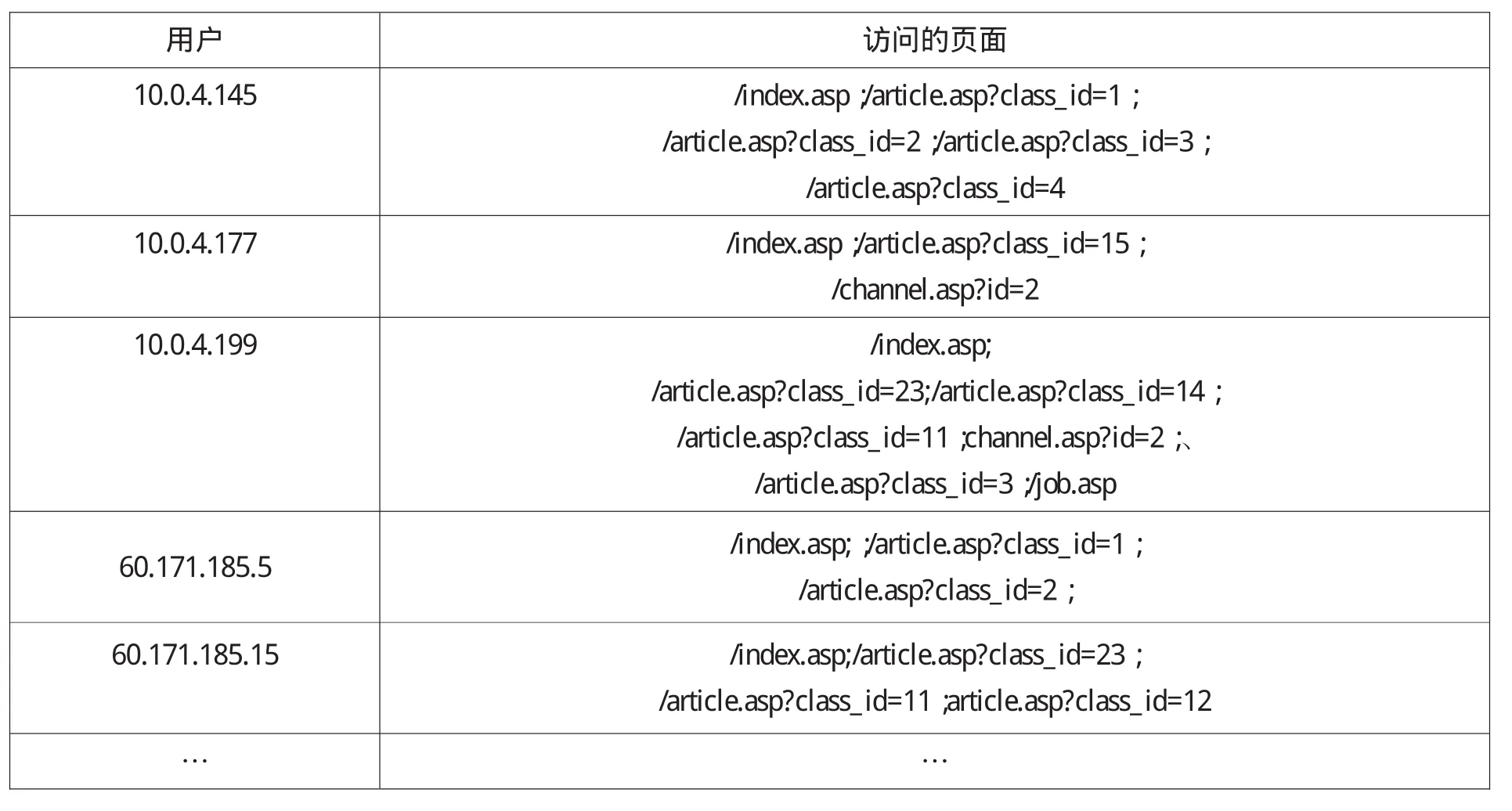
表1 净化后的数据

具体分析时，用A代表主页index.asp；B代表channel.asp?id=2；C代表/article.asp?class_id=1，后面都是通过class_id来区分不同的栏目；D代表class_id=2；E代表class_id=3；F代表class_id=4；G代表class_id=5；H代表class_id=6；I代表class_id=7……。生成的事务集如表2所示。然后在数据库中新建一个表，用于记录事务和访问者、IP的对应关系表。

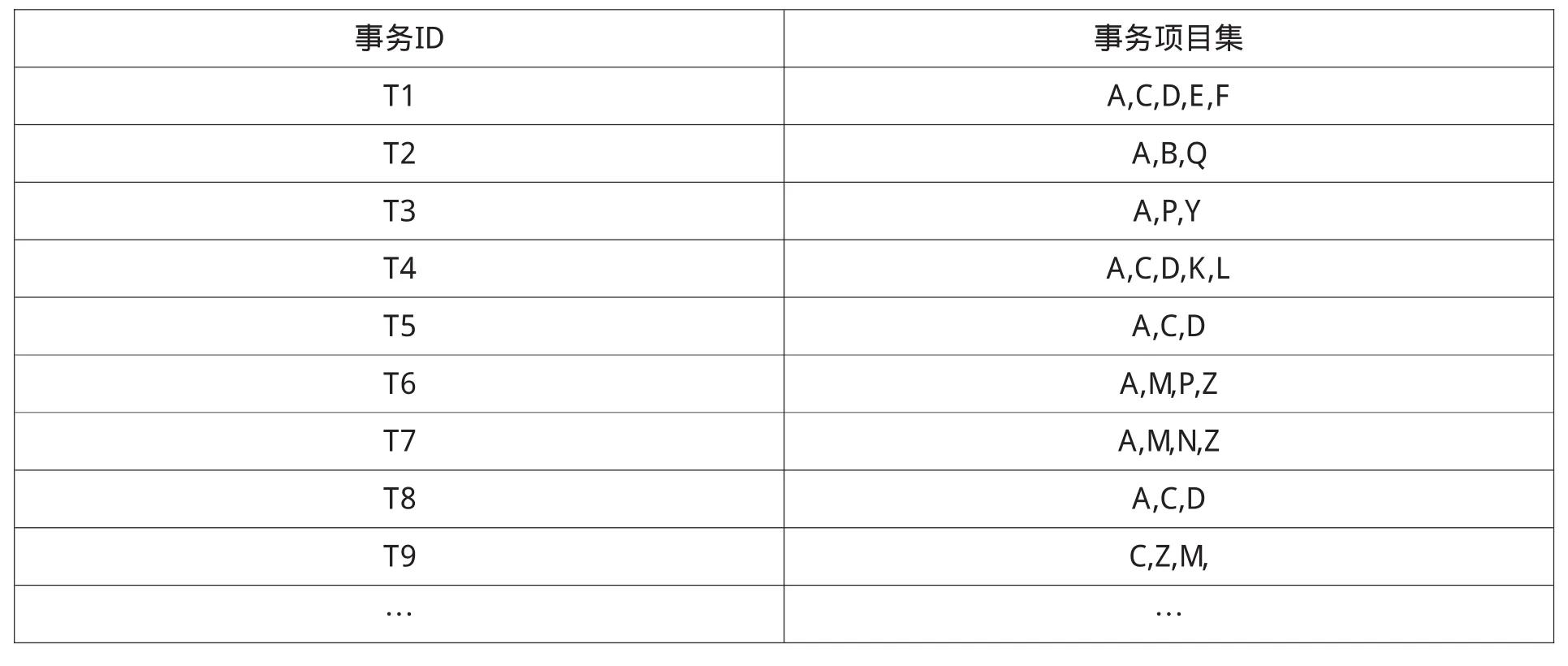
表2 就业网站事务集

在大量的数据中，选择一些典型的页面进行分析，如表3所示以及挖掘结果如表4所示。根据关联规则求得它们的支持度和置信度。

表3 网站分析

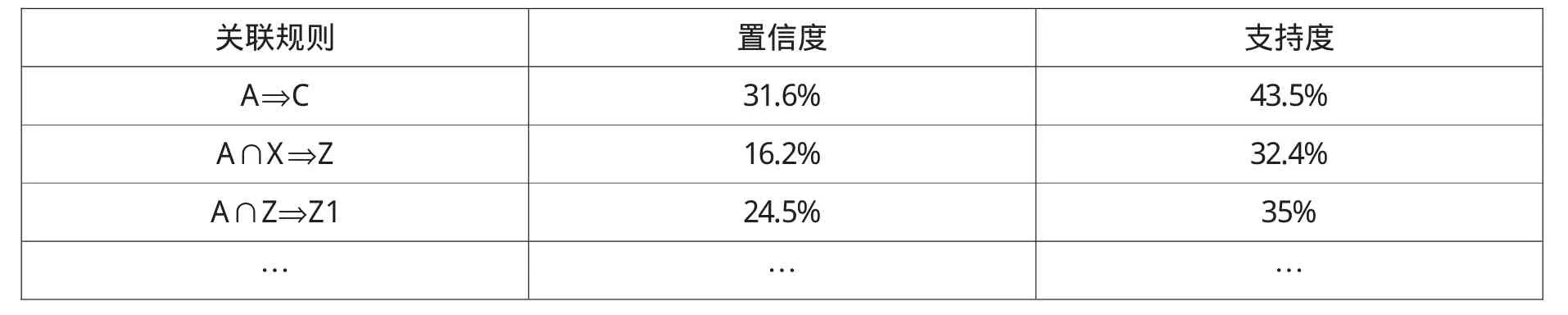
表4 选取的挖掘结果

其中showdl.asp?id=14这个网页是一个下载链接，它链接的内容是：安庆师范学院毕业生就业推荐表。A∩X圯Z表示访问同时访问主页和就业指导服务网页的人群中，有16.2%的人会去访问资料下载这个页面。6结语

网络时代的飞速发展，使网络上的数据呈几何数量级增长，数据挖掘的应用也越来越广泛。关联规则是数据挖掘中的一个重要的挖掘方法，虽然它有很多的不足，但还是能够找到一些方法加以改进。本文提出的基于矩阵的改进算法主要是基于事务压缩的思路来考虑的，在对数据库扫描的同时就开始给每个项目计数，因此对数据库只需要扫描一遍，这大大地提高了算法的效率。

[1]Agrawalr,Imielinskit,Swamia.Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACMS IGMOD International Conference on Management of Data.New York:ACMPress,1993:207-216.

[2]Jiawei Han,Micheline Kamber.数据挖掘:概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2007.

[3]梁循.数据挖掘算法与应用[M].北京:北京大学出版社,2006.

[4]陈文伟,黄金才.数据仓库与数据挖掘[M].北京:人民邮电出版社,2005.

[5]柴华昕,王勇.Apriori频繁项目集算法的改进[J].计算机工程与应用,2007,43(24):158-161,171.