层次分析法在家庭轿车选择中的应用

刘广会，齐化富，曹修文

随着居民消费水平的提高，选择一款适合自己的家庭轿车成为越来越多人的近期目标。由于各地治堵新政的出台、油价高等综合因素的影响，国内汽车市场需求增速回落。同时，购置税减免已经全部取消，技能汽车补贴的政策也即将收缩，微型和小型轿车挤占的市场空间将被归还给紧凑型车。中端汽车的下探和紧凑型汽车的不断推陈出新，汽车市场竞争激烈，居民收入的增加，使越来越多的人将将汽车消费档次上移，将起点定在紧凑型车。利用层次分析法（Analytic Hierarchy Process，AHP），可以在当前比较受关注的3款紧凑型车科鲁兹1.6L SL MT、朗逸1.6L手动品悠版、世嘉1.6L手动时尚版中选择最合适的家庭轿车。

层次分析法是美国运筹学家T.L.Saaty教授于20世纪70年代初期提出的一种简便、灵活而又实用的多准则决策方法。人们在对社会、经济以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的解决方法。以网络调查为基础，针对家庭轿车购置中的主要考虑因素建立层次结构图（图1）。

图1 家庭轿车购置考虑因素层次结构图

层次结构图反映了各因素之间的关系，使家庭轿车选购思维过程层次化。准则层中的各准则在目标决策衡量中所占的比重并不一定相同，在决策者心中各自占据一定比重。根据腾讯网汽车版网络调查结果，可以得到准则层五因素对目标层的成对比较矩阵：

该判断矩阵的最大特征向量归一后为a=（0.2492 0.2105 0.1918 0.1851 0.1633），经过一致性检验，CI=＜0.1，RI=1.12，CR=＜0.1一致性检验通过。

通过查阅三款车的官方报价，得到三款车对价格因素的成对比较矩阵：

该判断矩阵的最大特征向量归一后为a1=（0.3395 0.3362 0.3243），经过一致性检验，，RI=1.12，一致性检验通过。

通过腾讯网汽车频道调查资料，三款车型的综合油耗分别为8.6L，7.8L，8.7L，三款车在油耗方面的成对比较矩阵为：

该判断矩阵的最大特征向量归一后为a2=（0.3426 0.3108 0.3466），经过一致性检验，，RI=1.12，一致性检验通过。

在安全性因素方面，车的价位不同，而对于车中人而言，生命是等值的。抛开价格因素，一辆安全车应达到的最基本标准是：前后盘式制动系统、前排双气囊、三点式安全带、安全玻璃、高位刹车灯、ABS＋EBD(刹车防抱死和电子制动力分配系统)、车头、车尾可溃缩的安全车身设计，车门内有防撞杆、NCAP碰撞测试成绩等，选取三款车的主要安全配置、碰撞试验结果和刹车距离进行比较，得到表1。

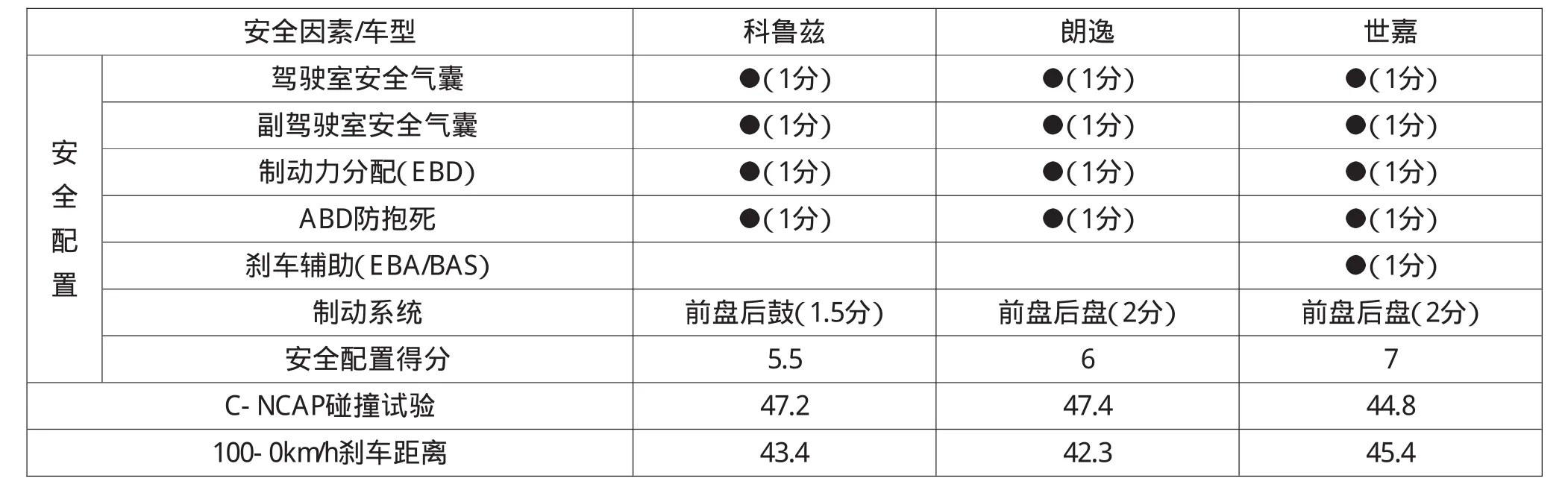
表1 三款车型主要安全因素

根据3款车的安全配置中各项分别赋分，得到安全配置对车辆安全性能的成对比较矩阵：

该判断矩阵的最大特征向量归一后为a31=（0.2973 0.3243 0.3784），经过一致性检验，，一致性检验通过。

该判断矩阵的最大特征向量归一后为a32=（0.3386 0.3400 0.3214），经过一致性检验，，一致性检验通过。

汽车的安全性与汽车的刹车距离成反比，由此得到三款车型的刹车距离倒数的成对比较矩阵：

该判断矩阵的最大特征向量归一后为a32=（0.3354 0.3441 0.3206），经过一致性检验，，一致性检验通过。

安全配置、碰撞试验和刹车距离三因素在保护乘员安全方面权重相同，取三因素均值归一化后作为三款车型安全因素的总体权重为：a3=（0.3700 0.3392 0.2907）。

对于三款车型的操控性能主要考察（性能配置、外观造型和舒适度），经查阅腾讯官网资料，找到三款车的网友评价（表2）。

表2 三款车型操控性能

由此可以得到三款车型对操控性能的成对比较矩阵：

该判断矩阵的最大特征向量归一后为a4=（0.3210 0.3047 0.3743），经过一致性检验，，一致性检验通过。

对于三款车型的维修服务，经查阅腾讯官网资料，找到三款车的网友评价，得到判断矩阵：

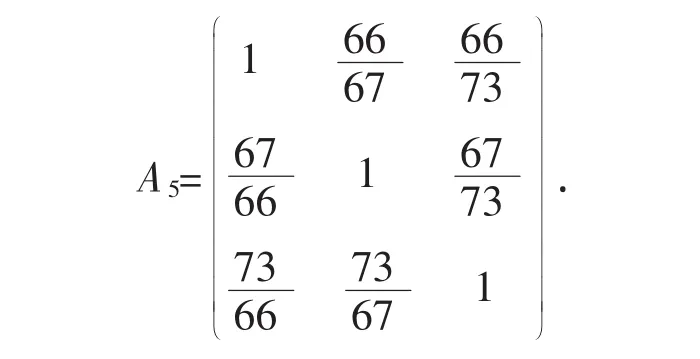
该判断矩阵的最大特征向量归一后为a5=（0.3204 0.3252 0.3544），经过一致性检验，，一致性检验通过。

由此可以得到三款车在价格、油耗、安全、操控性能和维修服务中所占的组合权重：

层次总排序为p×P=（0.3394 0.3238 0.3367）。由此可以的得到三款车的综合实力指标排序为别是：科鲁兹、世嘉和朗逸。整体看三款车型的总体实力相近，个人可以根据自己的偏爱和喜好从中选择适合自己的车型。

[1]谢季坚,刘承平.模糊数学方法及其应用[M].3版.武汉:华中科技大学出版社,2006:175-181.

[2]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社,2005:91-106.

[3]金菊良,魏一鸣,付强,等.计算层次分析法中排序权值的加速遗传算法[J].系统工程理论与实践,2002,22(11):39-43.

[4]常建娥,蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报:信息与管理工程版,2007(1):153-156.