粘钢加固损伤混凝土箱型桥墩的抗震性能Ⅱ:动力响应数值分析

邓江东 宗周红 黎雅乐 刘爱荣

(1广州大学土木工程学院,广州 510006)

(2东南大学土木工程学院,南京 210096)

地震是自然灾害中危害最大的灾种之一,桥墩作为桥梁结构中承受地震侧向力和竖向力的关键构件,在地震中易受到损毁.1995年日本阪神地震后,对3 396座桥梁钢筋混凝土桥墩进行震损调查,发现62%的桥梁轻微损伤或无破坏,25%中等程度损伤,5%严重破坏(可修复),8%倒塌或不可修复.2008年中国汶川地震中桥墩的损伤和破坏也是桥梁主要的震损形式之一[1].地震震害已经充分显示了桥墩在地震中的易损性以及在交通生命线工程中的关键地位,有必要对损伤桥墩抗震加固后的地震响应进行分析评价,以确保桥梁的抗震性能水平.

震后或者正常使用过程中桥墩往往会产生一定程度的初始损伤,目前关于加固损伤桥墩(包括结构柱)地震响应的研究资料较少.王维等[2]基于损伤因子建立了混凝土塑性损伤模型,考虑混凝土材料在动力荷载作用下的损伤演化,对钢筋混凝土桥墩进行了地震响应分析.程玲等[3]在加固锈蚀钢筋混凝土柱低周反复荷载试验的基础上,对加固锈蚀钢筋混凝土结构进行了动力时程分析,结果表明钢筋混凝土柱锈蚀后抗震性能降低,加固后有所恢复.刘海卿等[4]对FRP加固损伤厂房框架结构的抗震性能进行了有限元仿真模拟,结果表明FRP加固处理可明显提高结构的抗侧刚度,从而减小其地震响应.翁大根等[5]认为合理的布置耗能装置有利于地震能量在第一时间耗散,削减地震响应的第一峰值,并有利于地震能量向下部基础传递,从而提高结构的抗震性能.

有限元方法作为一种高效的数值分析工具,在钢筋混凝土桥墩的地震响应分析中起着越来越重要的作用[6-7].目前,对抗震加固弯曲损伤混凝土桥墩地震响应的研究工作还未见于文献资料.本文针对具有初始弯曲损伤的混凝土箱型桥墩,结合拟静力试验数据[8],采用柔度法和纤维模型,通过系统的地震响应数值分析,综合研究了混凝土箱型墩柱的抗震加固力学行为.

1 数值模型

1.1 基于柔度法的梁单元

柔度法可以保证梁单元的力平衡方程在整个计算过程中保持成立,并且单元可以在任意位置形成塑性铰,特别适合于强烈地震作用下考虑材料和几何双重非线性的模拟分析.Spacone等[9]对柔度法进行了较为系统的阐述,并给出了数值求解的具体方法.王占飞等[10]发现柔度法在地震响应分析中具有较高的计算精度.

1.2 数值模型的建立

1.2.1 材料本构模型

令混凝土的实际极限强度fc=37.5 MPa,相应的应变ε0=0.002;极限抗拉强度fcr=2.6 MPa,相应的应变εcr=0.000 1;达到极限应变后混凝土的强度取为0.1fc.考虑箍筋及加固钢板对混凝土的约束增强效果,约束区混凝土强度乘以放大系数1.2,混凝土采用Kent-Park本构模型[11].

钢材的屈服强度为335 MPa,弹性模量为200 GPa,采用Giuffré-Menegotto-Pinto本构模型.

1.2.2 单元划分

桥墩构造及分组见文献[8].墩顶集中质量根据轴压比确定,210 kN轴压下的墩顶集中质量为21 t,墩身质量按实际情况计算.桥墩分为加固段和未加固段,高度分别为H1和H2,加载的侧向力和竖向力分别为P和N,考虑由侧向变形Δ引起的二阶效应(见图1(a)).计算采用OpenSEES有限元程序,单元采用基于柔度法的非线性纤维梁柱单元,截面主要划分为保护层混凝土纤维(按无约束混凝土考虑)、核心区混凝土纤维(按约束混凝土考虑)、钢筋纤维和钢板纤维.未加固截面共有778根纤维(见图1(b)),加固截面共有808根纤维.

图1 桥墩计算简图

1.2.3 初始损伤的实现及地震动输入

图2 初始损伤分布

地震动输入采用有代表性的EL-Centro波、Kobe波和Northr波,且为X轴(强轴)、Y轴(弱轴)双向同步输入.为便于比较,峰值均设为0.22g.利用Newmark迭代法求解动力方程.

1.3 数值计算与试验结果的对比

数值计算得到的桥墩的荷载-位移滞回曲线与拟静力试验结果的比较见图3.由图可知,在弹性阶段、弹塑性阶段以及塑性发展阶段,试验结果与数值计算结果吻合较好,表明基于柔度法的非线性纤维梁柱单元在全过程中计算精度较高.

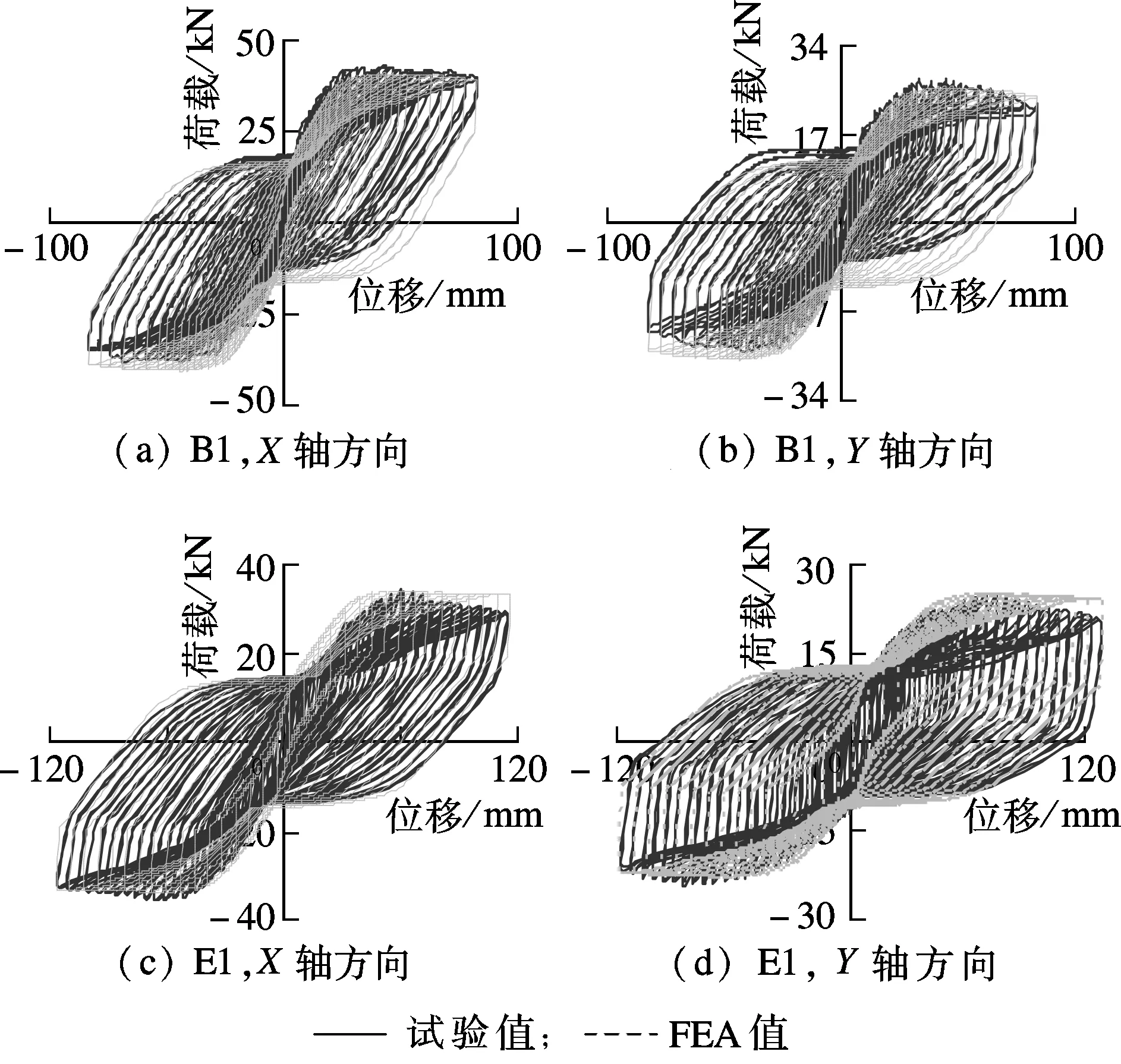
图3 荷载-位移滞回曲线

2 桥墩地震破坏模式

在EL-Centro地震波作用下计算得到的未加固桥墩A0、加固桥墩A1以及Ds=0.05时桥墩B3的钢筋最大应变响应沿墩高的分布，结果见图4.

图4 EL-Centro波作用下钢筋最大应变响应沿墩高分布

由图4可知,未加固桥墩钢筋应变地震响应的最大值发生在墩底区域;而加固桥墩钢筋应变响应的最大值发生在加固钢板的上缘,同时加固段的钢筋应变明显减小,表明采用较厚钢板加固后,即使墩底初始损伤严重,塑性铰仍会转移到加固钢板上缘,这与拟静力试验结果一致.Kobe波和Northr波作用下钢筋的最大应变分布规律与此一致.

3 地震响应规律

3.1 加固与未加固构件的比较

3.1.1 墩底地震剪力

EL-Centro波作用下,未加固桥墩A0与加固桥墩A1的墩底地震剪力响应时程见图5;3条地震波作用下桥墩的最大地震剪力值见表1.由图表可知,A1受到的墩底地震剪力较A0明显增大,其中X轴方向增大了1.29倍,Y轴方向增大了1.47倍.其原因在于,塑性铰出现在加固钢板上缘,在非线性阶段可以有效提高桥墩整体刚度,并显著改变桥墩的地震响应时程.

图5 EL-Centro波作用下的剪力响应时程

表1 最大地震剪力 kN

拟静力试验数据显示,加固后桥墩的极限承载力明显提高;在加速度为0.22g的地震作用下,A0和A1桥墩双轴方向的最大地震剪力均可能超过其极限承载力.

3.1.2 墩顶地震位移

EL-Centro波作用下,A0与A1桥墩墩顶位移的地震响应时程见图6;3条地震波作用下墩顶位移的最大值见表2.由图表可知,加固后桥墩的X,Y轴方向墩顶地震位移显著减小,分别为加固前的68%和79%,而拟静力试验数据显示加固后X,Y轴方向墩顶极限位移分别为加固前的1.29和1.51倍,这表明地震作用下加固桥墩的安全性显著提高.试件A0的Y轴方向地震位移(0.068 m)超过其极限变形能力(0.059 m),桥墩会发生破坏,加固后则处在安全范围之内.

3.1.3 震后剩余刚度

桥墩在地震作用下的荷载-墩顶位移滞回环见图7,剩余刚度定义为最大位移滞回环的刚度,即

图6 EL-Centro波作用下的墩顶位移响应时程

表2 墩顶位移地震响应 m

(1)

式中,±Δmax分别为最大位移滞回环正、反向加载时的峰值位移;±Fmax为±Δmax对应的荷载.

图7 EL-Centro波作用下的地震滞回曲线

地震作用下试件A0与A1桥墩的剩余刚度见表3.由表可知,加固后X,Y轴方向的剩余刚度均增大,分别为加固前的1.77和1.65倍,而拟静力试验数据显示加固后X,Y轴方向的剩余刚度为加固前的1.21和1.20倍,这表明地震作用下加固桥墩的安全性和震后性能大为提高,抗震性能储备增加.

3.2 关键影响参数分析

3.2.1 损伤程度影响分析

随着初始损伤程度从0增加到0.75,加固桥墩的柔性增大,构件的X轴向一阶自振周期从0.46 s增大到0.59 s,Y轴向从0.63 s增大到0.82 s.

图8中，Nt为墩底最大地震力，Lt为墩顶地震位移，Ft为剩余刚度.由图可知,随着损伤程度的增加,墩底最大地震剪力响应从整体来看略有降低,变化幅度在8%～-27%之间.墩顶最大地震位移响应从整体来看略有增加,变化幅度在29%～-7%之间,小于试验得到的极限位移,表明桥墩仍然处在安全范围之内.随损伤程度的增大,桥墩剩余刚度略有减小,但仍大于拟静力试验试件破坏时的最终刚度.

表3 剩余刚度地震响应 MN/m

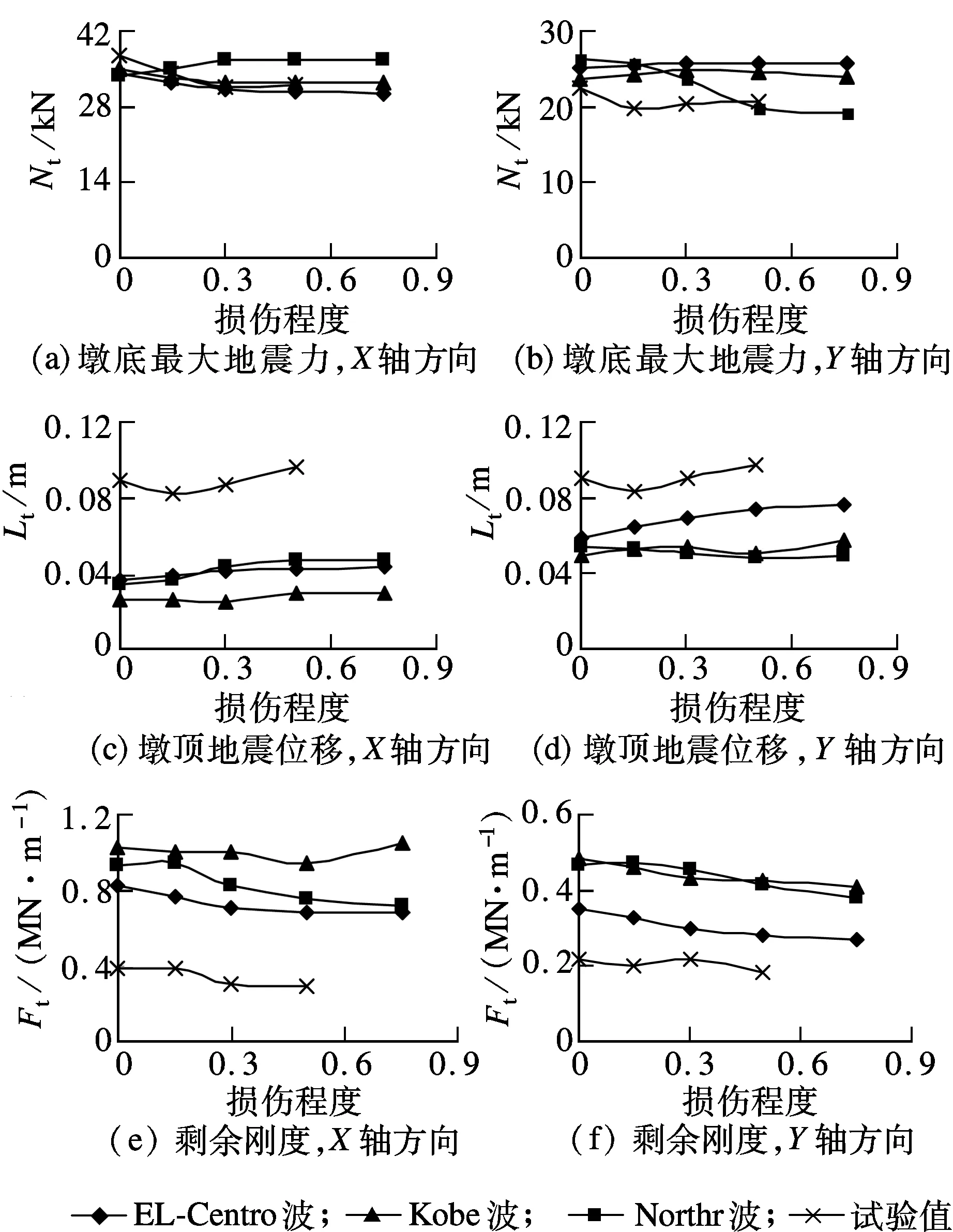
图8 损伤程度影响分析

总体来看,底部固结的加固方式可以有效地抵消墩底区域初始损伤的影响,因此初始损伤程度对桥墩地震响应的影响较小,这与拟静力试验的结论基本一致.此外,即使是在损伤程度较重的情况下,损伤桥墩加固后抗震性能仍能得到有效恢复.

3.2.2 加固厚度影响分析

加固钢板厚度影响分析见图9.未加固的C0试件X轴和Y轴方向的周期分别为0.56和0.78 s,5 mm钢板加固的C2试件X轴和Y轴方向的周期分别为0.48和0.65 s,表明在弹性阶段随加固钢板厚度的增加，桥墩刚度逐渐增大.

在非线性阶段,根据钢筋的应变分析,当加固钢板厚度小于1 mm时,在墩底形成塑性铰;当钢板厚度大于1 mm时,则在加固钢板上缘产生塑性铰.相比于在墩底产生塑性铰,加固钢板上缘产生塑性铰时桥墩的刚度显著增大,导致墩底剪力增加,墩顶位移减小,剩余刚度增加.

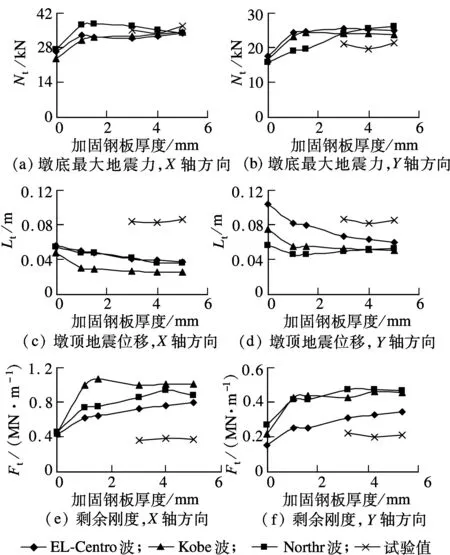
图9 加固钢板厚度影响分析

当加固钢板厚度大于1 mm时,控制段为加固钢板以上部分,粘钢加固段对整体抗震性能的影响减小,此时加固钢板厚度的增加对墩底剪力、墩顶地震位移及剩余刚度等指标影响不大.这与拟静力试验的结论基本一致.

3.2.3 轴压比影响分析

轴压比对抗震性能的影响分析见图10.由图可见,随着轴压比的增加,墩底地震剪力增加,墩顶变形量也快速增加.数值分析表明:轴压比为0.2时, EL-Centro波作用下墩顶地震位移超过其极限变形量而发生破坏,桥墩发生倾斜,且震后无法恢复到原位置.注意到在拟静力试验中随着轴压比的增加，墩顶极限位移逐渐降低,故增大轴压对桥墩抗震是极为不利的.

此外,随着轴压比的增加,剩余刚度快速减小,说明桥墩的破坏更为严重.此规律和拟静力试验结果正好相反,试验中随着轴压比的增大,试件的刚度和剩余刚度均增大.

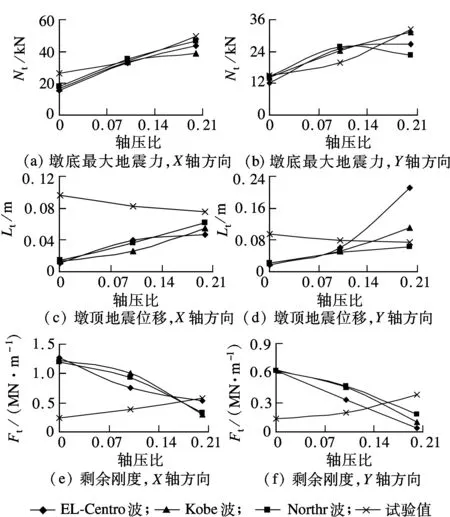
图10 轴压比影响分析

3.2.4 长细比影响分析

长细比影响分析见图11.随着墩高的增加,桥墩柔度增大,非线性情况下塑性铰长度也增加[12],从而导致地震剪力响应快速减小,最大位移响应增加,剩余刚度减小.

图11 长细比影响分析

4 地震响应与拟静力试验桥墩抗力的比较

4.1 地震剪力

试件分组可参考文献[8],采用试件墩底地震剪力与拟静力试验对应试件极限承载力的比值来表征地震作用下桥墩的安全程度,该比值称为归一化地震剪力.由图12可以看出，在0.22g地震加速度作用下,除试件D1,D2以及试件A1的X轴方向外,其他试件的归一化地震剪力均大于1,即超过了桥墩的极限承载力.

图12 归一化地震剪力

从双轴方向来看,相较于未加固桥墩A0,加固桥墩A1的X轴方向地震剪力安全度更大,Y轴方向则变化不明显,说明加固在一定程度上提高了桥墩对地震荷载的抵抗能力.

由于加固后塑性铰转移到加固钢板上缘,因此在加固区域中,损伤程度和加固钢板厚度的影响退到次要的位置.而随着轴压比和长细比的变化,桥墩地震剪力响应和极限承载力变化趋势一致,损伤程度、加固钢板厚度、轴压比和长细比等参数对地震剪力安全度的影响均不明显.

整体来看，Y轴方向归一化地震剪力较大,安全度较低.这与较低的Y轴极限承载力以及双轴之间地震作用的耦合有关.

4.2 墩顶地震位移

试件墩顶地震位移与拟静力试验对应试件极限位移的比值称为归一化墩顶地震位移.各试件的归一化墩顶地震位移对比分析见图13.

图13 归一化墩顶地震位移

相对于未加固桥墩A0，加固桥墩A1的地震变形量占其极限变形量的比例较低，构件的位移安全度较大.比如Y轴方向，Centro波作用下A0桥墩墩顶变形响应为其极限变形的1.67倍，而A1桥墩则仅为0.65倍.

桥墩的轴压比越大，其安全度越低，这主要是因为大轴压桥墩地震位移响应增大而其极限变形量减小.

随着长细比的增大，桥墩地震位移响应和极限变形量均增大，但增大幅度不同，位移安全储备略减小.

X轴方向各桥墩归一化地震变形均小于1，而Y轴方向的归一化地震变形较大，说明强震下Y轴方向更易于发生震损破坏.

4.3 震后剩余刚度

桥墩地震剩余刚度与拟静力试验试件剩余刚度的比值称为归一化剩余刚度.如图14所示,相对于未加固桥墩A0,加固桥墩A1的归一化剩余刚度较大,表明震后加固桥墩的剩余刚度安全度较大.

图14 归一化剩余刚度

损伤程度、加固钢板厚度和长细比等因素对剩余刚度安全度的影响不明显.大轴压情况下桥墩剩余刚度安全度显著减小;零轴压时桥墩震后破坏较轻,剩余刚度安全度也较大.

除试件D1外,其他试件的震后剩余刚度均大于1,表明地震后桥墩仍具有一定的刚度储备.综合来看,相比于X轴方向,Y轴方向的归一化剩余刚度较小,剩余刚度安全度较低.

5 结论

1) 地震作用下加固桥墩的易损位置为加固钢板上缘,这与拟静力试验结论一致.加固后,墩顶位移减少,剩余刚度增加,安全度提高,表明此加固方法是合理的.

2) 由于破坏控制塑性铰出现在加固钢板上缘,因此墩底加固区域的初始损伤程度对加固桥墩动力响应的影响不明显,表现为加固后几乎可以消除初始损伤的影响.

3) 加固钢板较薄时,塑性铰出现在墩底位置,导致墩底剪力和剩余刚度减小,墩顶位移响应增大.当钢板达到一定厚度时,塑性铰上移,对桥墩地震动力响应的影响显著减小.

4) 随着轴压比的增加,桥墩地震响应显著增大,墩底地震剪力、墩顶地震位移增加,剩余刚度减小.而随着长细比的增加,墩底地震剪力、剩余刚度减小,墩顶地震位移响应增加.

5) 初始损伤程度、加固钢板厚度和长细比对加固桥墩抗震安全度的影响较小.大轴压情况下,箱型桥墩的安全度快速降低.

6) 从安全度角度分析,地震作用下Y轴方向更易于发生破坏.

)

[1] 李乔,赵世春.汶川大地震工程震害分析[M].成都:西南交通大学出版社,2008.

[2] 王维,何丽丽,李涛涛,等.基于混凝土损伤塑性模型的桥墩地震响应分析[J].长江科学院院报,2012,29(6):79-82,86.

Wang Wei, He Lili, Li Taotao, et al. Seismic response of bridge pier based on plastic-damage model for concrete[J].JournalofYangtzeRiverScientificResearchInstitute, 2012,29(6): 79-82,86.(in Chinese)

[3] 程玲,贡金鑫,李金波.钢筋混凝土柱锈蚀及加固后的地震响应[J].工程抗震与加固改造,2012,34(3):31-39.

Cheng Ling, Gong Jinxin, Li Jinbo. Seismic response of corroded and strengthened RC structural column[J].EarthquakeResistantEngineeringandRetrofitting, 2012,34(3): 31-39. (in Chinese)

[4] 刘海卿,李海静,赵建军.碳纤维加固钢筋混凝土框架厂房及抗震分析[J].工业建筑,2012,40(12):102-106.

Liu Haiqing, Li Haijing, Zhao Jianjun. Analysis of anti-seismic performance of RC frame structure reinforced with CFRP[J].IndustrialConstruction, 2012,40(12): 102-106. (in Chinese)

[5] 翁大根,张瑞甫,张世明,等.基于性能和需求的消能减震设计方法在震后框架结构加固中的应用[J].建筑结构学报，2010,31(S2):66-75.

Weng Dagen, Zhang Ruifu, Zhang Shiming, et al. Application of energy dissipation method in post-earthquake RC frame retrofit based on performance and demand[J].JournalofBuildingStructures, 2010,31(S2): 66-75. (in Chinese)

[6] 艾庆华,王东升,向敏.基于纤维单元的钢筋混凝土桥墩地震损伤评价[J].计算力学学报,2011,28(5):737-742.

Ai Qinghua, Wang Dongsheng, Xiang Min. Seismic damage evaluation of RC bridge columns based on fiber elements[J].ChineseJournalofComputationalMechanics, 2011,28(5): 737-742. (in Chinese)

[7] 李正,李忠献.基于梁柱单元的钢筋混凝土桥墩地震损伤分析[J].天津大学学报,2011,44(3):189-195.

Li Zheng, Li Zhongxian. Seismic damage analysis of reinforced concrete bridge piers based on beam-column elements[J].JournalofTianjinUniversity, 2011,44(3): 189-195. (in Chinese)

[8] 宗周红,邓江东,黎雅乐,等.粘钢加固损伤混凝土箱型桥墩抗震性能Ⅰ:双向拟静力试验[J].东南大学学报:自然科学版,2013， 43(5)：944-951.

Zong Zhouhong, Deng Jiangdong, Li Yale, et al. Anti-seismic properties of damaged concrete bridge piers with hollow cross-section strengthened with adhering steel plates Ⅰ: bi-directional quasi-static test[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2013,43(5): 944-951.

[9] Spacone E, Ciampi V, Filippout F C. Mixed formulation of nonlinear beam finite element[J].Computers&Structures, 1996,58(1): 71-83.

[10] 王占飞,隋伟宁,吴权.E2地震作用下部分填充钢管混凝土桥墩非线性时程分析及抗震性能评价[J].工程力学,2011,28(S1):189-194.

Wang Zhanfei, Sui Weining, Wu Quan. Nonlinear time-history analysis and verification for seismic performance of partially concrete-filled steel bridge pier under E2 earthquake motion[J].EngineeringMechanics, 2011,28(S1): 189-194.(in Chinese)

[11] 过镇海.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003.

[12] 邓江东,宗周红,刘爱荣.粘钢加固钢筋混凝土箱型桥墩双向恢复力模型研究[J].工程力学,2014.(待刊出)

Deng Jiangdong, Zong Zhouhong, Liu Airong. Study on bi-directional model of restoring force of hollow reinforced concrete piers strengthened by adhering steel plates[J].EngineeringMechanics, 2014, to appear. (in Chinese)