基于面内位移测量和刚体旋转的形貌测量方法
2013-12-26代祥俊戴美玲杨福俊卢位昌姚亚卿
代祥俊 戴美玲 杨福俊 卢位昌 姚亚卿
(东南大学土木工程学院,南京 210096)
三维形貌测量在质量检测等工业应用方面起着重要的作用.光学测量技术因其具有非接触、高精度等优点,被广泛应用于形貌测量中.常见的光学测量方法包括影栅云纹、投影栅线、立体视觉、干涉方法等.在影栅云纹法中,试件栅和参考栅相互叠合形成云纹,此处的试件栅并不是单独的栅,而是参考栅在光线照射下投射在物体表面而形成的参考栅的影像,它包含了物体的形貌信息,其形状随物体表面形状的改变而变化[1].条纹投影技术是指,以单频或多频光栅产生的光场投影到待测物体表面,从另一个角度观测物体反射回来的光栅条纹,并进行计算、分析从而提取出三维面形信息[2].条纹投影技术通常与Fourier变换技术、相移技术和数字图像相关方法(digital image correlation, DIC)结合使用[3-7].立体视觉是另外一种广泛使用的三维形貌测量方法,它采用2个或者多个相机,从不同的角度同时采集物体图像,通过匹配计算获得形貌[8].干涉方法广泛应用于面内和离面位移测量中,近年来也被频繁应用到物体轮廓测量中[9-12];该方法不需要投影栅线,形貌信息包含在散斑颗粒内,也不需要进行多个相机的标定.
大部分形貌测量方法的最终目的是测得物体表面各点的三维坐标(x,y,z)[13].一旦获取了不同(x,y)处z方向的坐标,物体表面的三维形貌即可确定.事实上,z(x,y)可看作物体表面的相对高度.本文提出了一种基于面内位移和刚体旋转2个要素获取物体三维形貌的方法.通过旋转物体获得刚体位移,根据位移和相对高度的关系得到物体形貌.面内位移的测量方法采用了电子散斑干涉法(electronic speckle pattern interferometry,ESPI)和数字图像相关法(DIC).实验结果验证了该方法的有效性和可靠性.
1 基本原理
1.1 电子散斑干涉法
电子散斑干涉法是一种常用的位移测量方法.图1为典型的面内位移测量光路图.图中,激光器发出的光被分光镜分为两束光,其中一束为物光,经反光镜、扩束镜后照射到试件上;另一束为参考光,经反光镜、扩束镜后照射到试件上,与物光在试件表面相干形成干涉条纹.同时,利用CCD摄像头对干涉条纹进行实时采集,并传输到计算机中.实验时,分别采集变形前后的干涉图像,将其相减得到实时的干涉条纹.通常,干涉条纹可表示为
I(x,y)=a(x,y)+b(x,y)cosφ(x,y)
(1)
式中,a(x,y)为背景光强;b(x,y)为条纹幅值;b(x,y)/a(x,y)为条纹对比度;φ(x,y)为物体变形引起的位相变化,即待求位相.

图1空间载波法光路图
位相分布和面内位移的关系为

(2)
式中,λ为激光波长;u为x方向上的面内位移;θ为入射角.可见,u场位移可以通过计算位相分布φ(x,y)得到.
空间载波方法(spatial-carrier method,SCM)是一种常用的位相测量技术.其基本思想是在干涉条纹上叠加一个载波条纹,通过偏转光学器件(如图1中的载波片)或物光产生一个附加位相.一个载波条纹图通常可表示为
I(x,y)=a(x,y)+c(x,y)ei2πf0x+c*(x,y)e-2πf0x
(3)
式中,c(x,y)=b(x,y)eiφ(x,y);f0为x方向上的载波频率.Fourier变换法是空间载波法中一种较常用的求取位相的方法[14].使用Fourier变换法可得
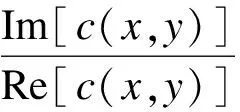
(4)
1.2 数字图像相关法
DIC法是一种广为人知的光学测量方法,通过处理变形前后被测物体表面的数字图像获得位移信息,其基本原理如图2所示.变形前采集一幅图像作为参考图像,变形后采集一系列图像作为目标图像.在参考图像中,以某点为中心,选取一定大小的区域作为子区,通过数值计算,在各个目标图像中寻找相应的子区,以确定该点的位移.计算时相关函数的选择尤为重要,本文使用归一化最小平方距离相关函数C来评价变形前后图像子区的相似程度[15-16],即
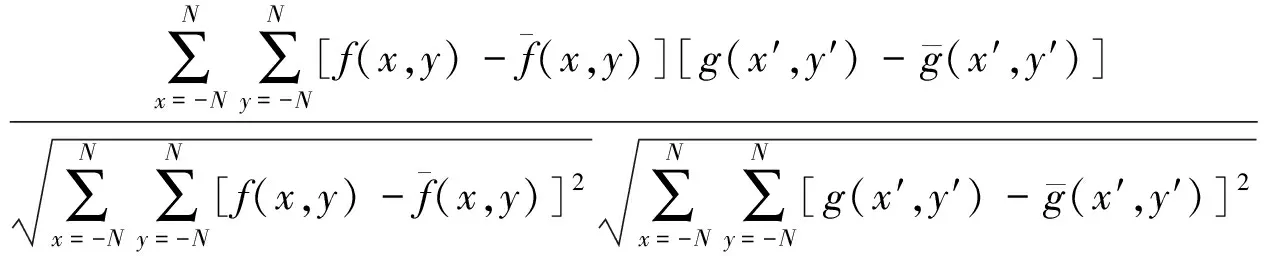
(5)

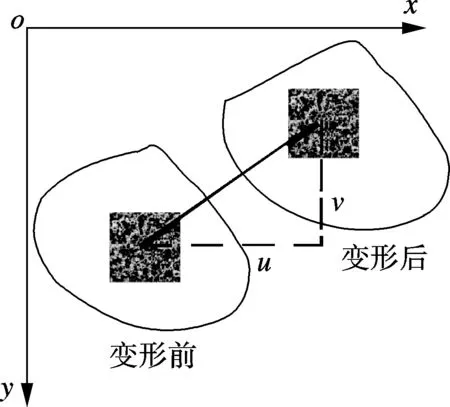
图2 变形前后图像子区示意图
1.3 三维形貌的获取
当物体发生旋转时,表面上的点会产生相应的刚体位移,并且不同高度的点产生的位移各不相同,通过测定各点的位移即可确定相对高度.相对高度和面内位移的关系如图3所示.假设试件旋转的角度为α,试件表面任意点水平方向上的坐标为x,其相对高度可通过下式得到:

(6)
将式(2)和(4)代入式(6),可得

(7)
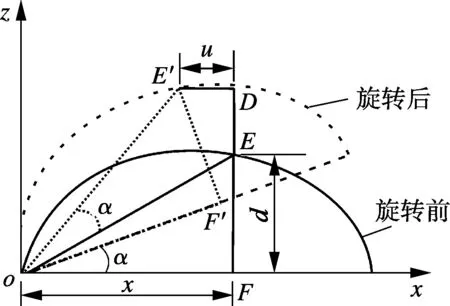
图3 相对高度和面内位移的关系
这样,只要通过电子散斑干涉法测出面内位移,即可通过式(7)得到物体的形貌.同理,通过数字图像相关法测出位移后,可通过式(6)得到物体的形貌.
2 实验系统
2.1 电子散斑干涉系统
电子散斑干涉系统采用的激光器是功率为50 mW、波长为632.8 nm 的He-Ne激光器.如图1所示,激光器发出的光经分光镜后被分为物光和参考光.物光被扩束后照射在物体上;参考光经反射后进入另一个扩束镜,扩束后的光经过一个用来产生载波条纹的载波片后照射在物体上.两束光在物体表面发生干涉,采用实时相减技术,便可在监视器上观测到干涉条纹.图像采集是通过分辨率为881×508像素、灰度为8 bit的CCD来实现的.
2.2 数字图像相关系统
图4给出了数字图像相关实验系统示意图.试件安置在旋转平台上,并通过步进电机来驱动其转动.步进电机的基本步距角为1.8°,通过调整微控制器可将步距角设置为0.9°,经细分设置后精度达到1.4′.实验时,可根据需要控制平台的旋转方向为逆时针或顺时针.系统使用的采集装置是灰度为8 bit、分辨率为1 280×1 024像素的CCD.

图4 DIC实验系统示意图
3 实验验证
本文采用基于面内位移测量和刚体旋转2个要素的方法,测量物体的三维形貌,被测试件是半径为15 mm、边缘有倒角的半圆柱(见图5).实验时选择的角度为0.9°,面内位移分别采用数字图像相关法和电子散斑干涉法中的空间载波法测定得到.

图5 被测试件
在空间载波法中,通过旋转载波片来产生载波条纹.图6(a)为典型的背景载波条纹;图6(b)和(c)分别为被载波调制后未旋转和旋转的条纹图.利用Fourier变换算法和解包裹技术,可获得解包裹的位相分布.未解包裹和解包裹的位相图分别见图6(d)和(e).根据位相和位移的关系,求得u场的刚体位移,结果见图7.由此便可得到物体的形貌,结果见图8.

图6 干涉条纹图

图7 u场位移分布图

图8 由ESPI法获得的物体形貌
在数字图像相关法中,为了测量旋转产生的u场位移,需要在旋转前采集一幅图像作为参考图像,旋转15°后采集相应的目标图像.采用相关算法,便可求得u场位移,从而得到如图9所示的物体形貌.进行相关计算时,图像子区大小为41×41像素,相邻计算点距离为5像素.
为了验证本文方法的准确性,选取了试件上2个不同位置的实验值与游标卡尺测量值进行对比.
位置A和B分别为试件边缘和靠中间部位,如图5所示.图10(a)和(b)分别为试件上2个不同位置的高度数据对比曲线.根据对比曲线可以发现,实验值和游标卡尺测量值很接近.对于边缘的位置A,ESPI法测得的最大误差小于1.20%,DIC法测得的最大误差小于1.75%.对于位置B,ESPI法和DIC法的最大误差分别小于0.50%和1.00%.

图9 由DIC法获得的物体形貌

图10 不同位置的物体轮廓比较
4 结语
本文提出了一种基于面内位移测量和刚体旋转2个要素的三维形貌测量方法.通过精确旋转试件可产生相应的刚体面内位移,并分别采用电子散斑干涉方法中的空间载波法和数字图像相关方法对其进行测量.利用面内位移和相对高度的关系,得到物体形貌.实验结果证明了该方法的有效性和可靠性.在空间载波法中,旋转试件实现了对载波条纹的调制,可通过控制旋转的角度来实现载波频率的调整.考虑到相干条件,旋转的角度要控制在较小的范围内.使用数字图像相关法时,物体旋转角度的选择范围要比空间载波法大.对于本文方法在大试件、360°形貌测量方面的应用有待于进一步研究.
)
[1] Quan C, Fu Y, Tay C J. Determination of surface contour by temporal analysis of shadow moiré fringes [J].OpticsCommunications, 2004,230(1/2/3): 23-33.
[2] Dai M, Yang F, He X. Single-shot color fringe projection for three dimensional shape measurement of objects with discontinuities [J].AppliedOptics, 2012,51(7): 2062-2069.
[3] Yi J, Huang S. Modified Fourier transform profilometry for the measurement of 3D steep shapes [J].OpticsandLasersinEngineering, 1997,27(5): 493-505.
[4] Yang F, Dai M, He X, et al. Single fringe projection profilometry based on sinusoidal intensity normalization and subpixel fitting [J].OpticsandLasersinEngineering, 2011,49(3): 465-472.
[5] Zhang S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques[J].OpticsandLasersinEngineering, 2010,48(2): 149-158.
[6] Pan B, Xie H, Gao J, et al. Improved speckle projection profilometry for out-of-plane shape measurement [J].AppliedOptics, 2008,47(29): 5527-5533.
[7] Zhu F, Liu W, Shi H, et al. Accurate 3D measurement system and calibration for speckle projection method [J].OpticsandLasersinEngineering, 2010,48(11): 1132-1139.
[8] Orteu J J. 3D computer vision in experimental mechanics [J].OpticsandLasersinEngineering, 2009,47(3/4): 282-291.
[9] Mirza S, Shakher C. Surface profiling using phase shifting Talbot interferometric technique [J].OpticalEngineering, 2005,44(1): 013601.
[10] Genovesea K, Lambertib L, Pappalettere C. A comprehensive ESPI based system for combined measurement of shape and deformation of electronic components [J].OpticsandLasersinEngineering, 2004,42(5): 543-562.
[11] Quan C, Chen W, Tay C J. Shape measurement by multi-illumination method in digital holographic interferometry [J].OpticsCommunications, 2008,281(15/16): 3957-3964.
[12] Pedrinia G, Fröninga P, Tiziania H J, et al. Shape measurement of microscopic structures using digital holograms [J].OpticsCommunications, 1999,164(4/5/6): 257-268.
[13] Su X, Zhang Q. Dynamic 3D shape measurement method: A review [J].OpticsandLasersinEngineering, 2010,48(2): 191-204.
[14] Malacara D, Thompson B J.Handbookofopticalengineering[M]. New York: Marcel Dekker Inc., 2001: 397-398.
[15] Pan B. Recent progress in digital image correlation [J].ExperimentalMechanics, 2011,51(7): 1223-1235.
[16] Pan B, Qian K, Xie H, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J].MeasurementScienceandTechnology, 2009,20(6): 1-17.
