基于粗粒度可重构架构的并行FFT算法实现

曹 鹏 杨锦江 梅 晨

(东南大学国家专用集成电路系统工程技术研究中心,南京 210096)

以无线通信和媒体处理为代表的数据流应用对硬件架构平台的性能提出了较高的要求.DSP(digital signal processer)灵活性好,但由于采用串行计算模式,难以满足高性能的需求.ASIC(application specific integrated circuit)能针对特定应用定制数据通路和运算模块,并能提供很好的性能,但难以迅速适应新的应用或当前应用的更新.可重构兼具ASIC的高性能和DSP的高灵活性,通过将运算任务映射到硬件资源上,保证了执行的高并行度,同时能够根据应用变化通过配置改变其功能,因此得到广泛采用[1].与细粒度可重构架构FPGA相比,粗粒度可重构架构[2]的区别在于将FPGA中的LUT替换成粗粒度的运算单元,同时简化了FPGA的互联类型.近年来众多粗粒度可重构架构[2]被提出并得到应用.例如,XPP和ADRES架构已经被应用于无线通讯[3-4]和媒体处理[5-6]领域.而作为数字信号处理中的核心运算单元,FFT已经在很多粗粒度可重构架构上被实现,如NoC[7],MorphoSys[8],SmartCell[9], ePUMA[10]等.REMUS_LPP(reconfigurable embedded multimedia system, low performance processor)是可重构嵌入式媒体处理系统的移动版本,已被应用于媒体[11-12]和人脸检测[13]等算法.本文基于REMUS_LPP实现了并行化的FFT算法,并提出了流水气泡消除和数据块位置重排优化技术.实验结果显示,本文的FFT性能明显优于同类并行架构,并有效降低了片上存储需求.

1 REMUS_LPP架构特征

1.1 REMUS_LPP架构

REMUS-Ⅱ是面向流处理应用的大规模粗粒度可重构阵列.REMUS_LPP作为其移动版本,与REMUS-Ⅱ[12]具有类似的架构,区别在于为了追求更高的能量效率,前者的运算资源为后者的一半.

REMUS_LPP架构的框图如图1所示,主要包括3个关键模块:用来加速计算密集型任务的可重构处理单元(reconfigurable computing unit,RPU)、用来加速控制密集型任务的微处理器单元(micro processing unit,μPU)和用于系统总体控制调度的主控核ARM.RPU接收μPU或主控核发出的配置信息,按照配置信息进行相应的运算.系统中还包含一些辅助模块,如中断控制器(IntCtrl),DMA控制器和EMI等.这些模块都通过AHB总线相连,另外在RPU和μPU之间采用一个专用数据通路来实现配置信息在2个模块间的高速传输.

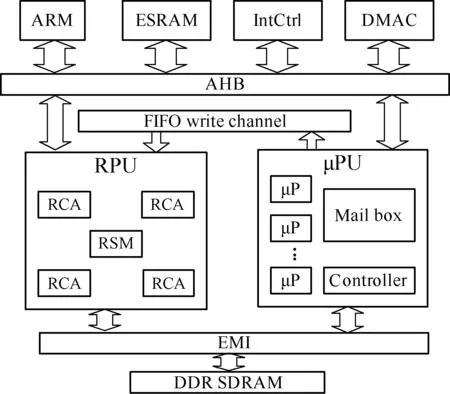
图1 REMUS_LPP架构框图

1.2 RPU

RPU主要用来加速执行密集型的计算任务,其内部结构如图1所示.RPU结构包含4个可重构运算阵列 (reconfigurable computing array, RCA)和一个RPU共享存储器(RPU shared memory, RSM).RCA作为动态可重构计算单元,包含一个运算阵列(processing element array，PEA)、一个RCA输入FIFO和一个RCA输出FIFO(RIF与ROF)、一个常数存储器(constant memory, CM)和一个RCA中间数据缓存(RCA internal memory, RIM),如图2(a)所示.PEA的结构如图2(b)所示,主要由一个8×8的PE(processing element)阵列和8×8的TR(temporary register)阵列组成,数据可以从上一层的PE或TR传输到下一层PE或TR中.每个PE实现了简单的ALU功能,TR作为阵列内的分布式存储器主要用来暂存运算的中间数据以减少流水的气泡.由RSM,RIM和TR构成的存储子系统保证了数据在RPU中传输的高效性.

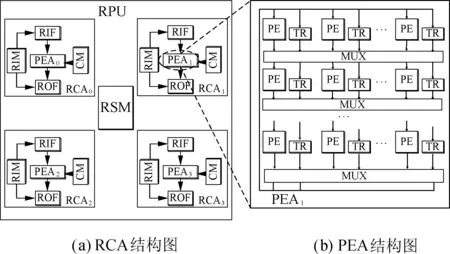
图2 RPU内部结构图

1.3 μPU

由图1可见,μPU包含一个微处理器阵列(micro processing element array，μPEA)和一个邮箱.μPEA主要用来处理控制密集的任务,如生成配置信息等.μPE之间的通信以及μPE与主控之间的通信通过邮箱完成.μPU在生成配置信息后通过专用数据通路传输到RPU.

2 FFT算法在REMUS_LPP上的实现

离散傅里叶变换(DFT)是数字信号处理领域的经典算法之一,可表示为

式中,N为点数;旋转因子WN可由下式计算获得:

WN=e-2πj/N

快速傅里叶变换(FFT)[14]将传统离散傅里叶变换的计算量从N2大幅降低到Nlog2(N),但依旧是诸多应用中计算的瓶颈.本文提出一种基于粗粒度可重构架构的FFT实现方案.

根据输入数据的不同,FFT通常可分为按时间抽取(DIT)和按频率抽取(DIF)2种.鉴于DIT算法能在蝶形运算的2个分支上获得更好的计算平衡,本文采用经典的基2FFT算法,从而将N点FFT分为log2(N)个步骤完成,每个步骤执行N/2个2点的DFT.实现该步骤的执行单元被称为蝶形运算单元(BU),其基本运算公式如下:

Aout=Ain+BinW

Bout=Ain-BinW

式中,输入Ain,Bin和输出Aout,Bout以及旋转因子W都为复数.在算法映射过程中,BU运算被分解为多个实数运算,包括4次加法、2次减法和4次乘法,具体过程如下:

Tmpre=Bin_reWre-Bin_imWim
Tmpim=Bin_reWim+Bin_imWre
Aout_re=Ain_re+Tmpre
Aout_im=Ain_im+Tmpim
Bout_re=Ain_re-Tmpre
Bout_im=Ain_im-Tmpim

式中,Ain_re和Ain_im为输入Ain的实部和虚部;Bin_re和Bin_im为输入Bin的实部和虚部;Aout_re和Aout_im为输出Aout的实部和虚部;Bout_re和Bout_im为输出Bout的实部和虚部;Tmpre,Tmpim和Wre,Wim分别表示中间结果和旋转因子的实部和虚部.

2.1 算法并行化

在本文设计中,输入数据首先经过位反转排序,然后通过2个步骤完成FFT算法.第1步可被称为局部串行FFT,输入数据被等分为p个数据块,每个N/p的数据块在编号为0～p-1的执行单元(EU)中独立执行,分别完成N点FFT的前log2(N/p)阶,计算结果存储在每个EU的局部存储器中,伪码如算法1所示.第2步可被称为数据交换FFT,每个EU只将其上半部分和下半部分的N/(2p)的数据和其配对的EU进行交换,完成N点FFT中剩余的log2p阶计算,运算完成后再按同样的交换规则写回到对应的EU,从而保证下一阶运算进行数据交换的统一性,伪码如算法2所示.

算法1局部串行FFT

1 Inputc=(c0,c1,…,cN/p-1)

2 Outputc=(c0,c1,…,cN/p-1)

3 fori=0 to log2(N/p)-1

4l=2i

5 fork=0 toN/p-1

6 getwbyjandi

7 if((i*N/p+k)modl=(i*N/p+k)mod 2l)

8c(k)=c(k)+c(k+l)*w

9c(k+l)=c(k)-c(k+l)*w

10 end if

11 end for

12 end for

算法2数据交换FFT

1 Inputc=(c0,c1,…,cN/p-1)

2 Outputc=(c0,c1,…,cN/p-1)

3j=log2(p)+1

4 fore=0 to log2(p)-1 do

5t=2e,v=2j,j=j-1

6 fori←0 top-1 do

7 if (imodt=imod 2t) then

8 Send upperN/(2p) data stored inc[N/(2p)]-c[N/p-1] to the (i+p/v)-th PE.

9 ReceiveN/(2p) data from (i+p/v)-th PE and store them to upperN/(2p) location ofc[].

/*transform*/

10 fork←0 toN/(2p)-1 do

11 getwbyi,kande

12c[k]=c[k]+c[k+N/(2p)] *w

13c[k+N/(2p)]=c[k]-c[k+N/(2p)]*w

14 end for

15 Send upperN/(2p) of transformed data stored inc[N/2p]-c[N/p-1]back to the (i+p/v)-th PE.

16 Receive theN/2ptransformed data from (i+p/v)-th PE and store them back to upperN/(2p) location ofc[].

17 else

18 Send lowerN/(2p) data stored inc[0]-c[N/(2p)-1] to the (i-p/v)-th PE.

19 ReceiveN/(2p) data from (i-p/v)-th PE and store them to lowerN/(2p) location ofc[].

/*transform*/

20 fork←0 toN/(2p)-1 do

21 getwbyi,kande

22c[k]=c[k]+c[k+N/(2p)]*w

23c[k+N/(2p)]=c[k]-c[k+N/(2p)]*w

24 end for

25 Send lowerN/(2p) of transformed data stored inc[0]-c[N/(2p)-1]back to the (i-p/v)-th PE.

26 Receive theN/(2p) transformed data from (i-p/v)-th PE and store them back to lowerN/(2p) location ofc[].

27 end if

28 end for

29 end for

2.2 流水气泡消除

BU的数据流图(DFG)如图3(a)所示.由图可见,BU运算可利用10个PE在3个周期内完成2点FFT的计算.由于每个RCA中包含规模为8×8的PE阵列,因此能同时实现4个BU.BU的执行过程如图3(b)所示,分为读入、计算和写出3个步骤,其中计算步骤通过3个计算周期完成.虽然输入A和输入B可被同时传输至运算阵列PEA,但是输入A在第3个计算周期才被使用,这样使得下一次的输入需要等待3个周期才可以进行,产生了流水气泡.

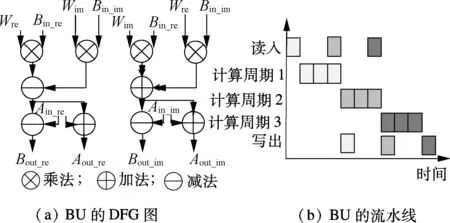
图3 优化前的蝶形运算单元DFG图和流水线

为了提升BU执行效率,对BU的DFG通过插入寄存器的方式进行优化,优化后的DFG如图4(a)所示.将优化后的DFG映射至RCA时,插入的寄存器采用临时寄存器TR实现,从而保证所有数据输入可以连续进行.改进后的BU流水线如图4(b)所示,和图3(b)所示的流水线相比,BU的执行效率大幅提高.

图4 优化后的蝶形运算单元DFG图和流水线

2.3 数据块重排

本文将每个RCA作为FFT算法中的EU,共可实现4个EU,每个EU可实现4个BU.每个N/4点子序列存储在各个RCA的RIM中.

N点FFT共需要进行m阶运算(m=log2N),其前log2(N/4)阶运算在4个RCA中独立并行执行,并将运算结果存储在各自的RIM中.在执行第m阶和第m-1阶运算时,RIM中的数据被分为上半部分和下半部分,并通过共享存储器RSM进行数据交换,交换方式如图5所示,其中RIM0～RIM3分别为RCA0～RCA3中的临时数据缓存RIM,不同的数字标识RIM中数据的上半部分或下半部分.在进行第m-1阶运算前,RIM0～RIM3中的数据块位置如图5(a)所示.为进行第m-1阶运算,RCA间需先进行数据交换,交换完成后的数据块位置如图5(b)所示.当第m-1阶运算完成后,各个RIM中的数据再次进行交换,交换完成后的数据块位置如图5(a)所示.第m阶的执行过程与第m-1阶类似,其数据交换后的数据块位置如图5(c)所示.

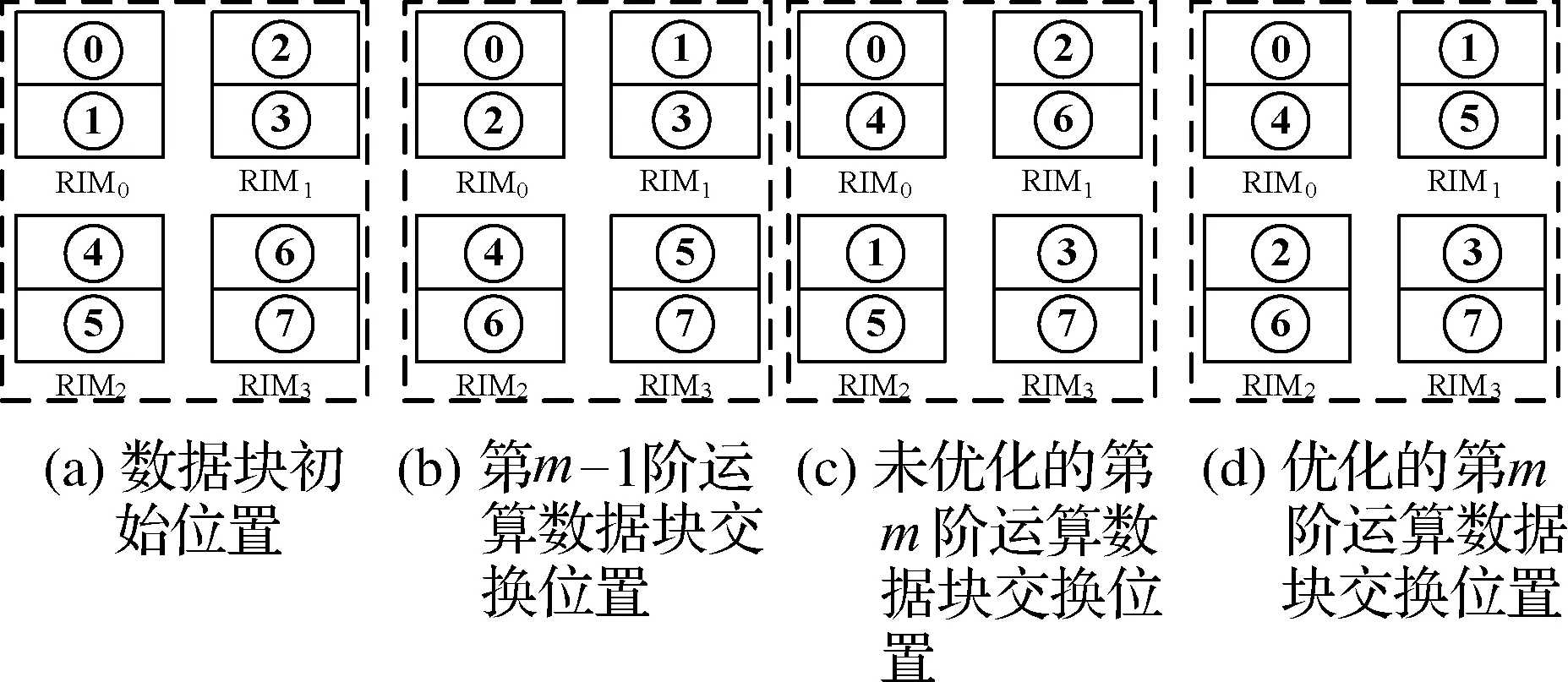
图5 数据块位置图

分析图5(a)～(c)可见,在数据块组成形式由图5(b)(针对第m-1阶运算)重排为图5(c)(针对第m阶运算)过程中,考虑到4个RCA均可实现任意数据的第m阶运算,可不必将第m-1阶运算的结果写回为图5(a)的形式,而直接对数据块位置进行重排,以满足第m阶运算的需求.优化的数据块重排方式如图5(d)所示,由图可见,4组RIM中的数据虽然分布在不同的RCA中,但是其组织形式与图5(c)无异.通过采用数据块重排的技术,FFT最后2阶计算中的数据不需要将结果写回,从而有效地减少了RCA间数据传输量.

3 结果和比较

3.1 性能分析和实现

基于可重构架构REMUS_LPP实现N点并行FFT运算时,所需时间T可表示为

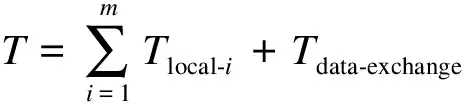
式中,Tlocal-i表示在N点FFT运算过程中,第i(i=1,2,…,m)阶运算在RCA上执行的时间;Tdata-exchange表示RCA间进行数据交换的时间,只在最后2阶FFT运算中发生;Tlocal-i包括旋转因子更新时间TW-update、计算时间Tcalc和数据读取写出时间Tload-store;Tdata-exchange包括数据传输时间Tdata-transfer和同步时间Tsync.

各阶运算执行中读入-计算-写出的流水如图6所示.在计算开始前,需要读入处理数据并完成旋转因子更新,后者更新频度与阶数有关,因此整个读入-计算-写出流水与阶数有关.第m～m-2阶FFT运算的流水线如图6(a)所示.由于数据传输完全被旋转因子的更新打断,因此读入、计算与写出完全串行,执行时间由旋转因子的更新时间决定.第m-3阶FFT运算的流水线如图6(b)所示.虽然读入和计算的时间有部分重叠,但流水线依旧被旋转因子的更新打断,不同旋转因子对应的数据块之间的计算完全没有重叠时间,导致数据不能连续输入.而在其余阶的运算中,由于旋转因子更新频度较低,因此其更新时间可被完全隐藏在计算流水中.第4阶FFT运算的流水线如图6(c)所示,需要更新2次旋转因子.由于每个RCA上4个BU最多需要4个不同的旋转因子,因此最多需要4个周期完成各个旋转因子的更新.随着每次旋转因子的更新,需要完成一半数据的传输,传输时间为N/64个周期.在图6(c)中,数据传输时间大于旋转因子更新时间,从而使得后者完全被掩盖在读入-计算-写出的流水线中,保证了数据的读入、计算和写出完全流水执行.

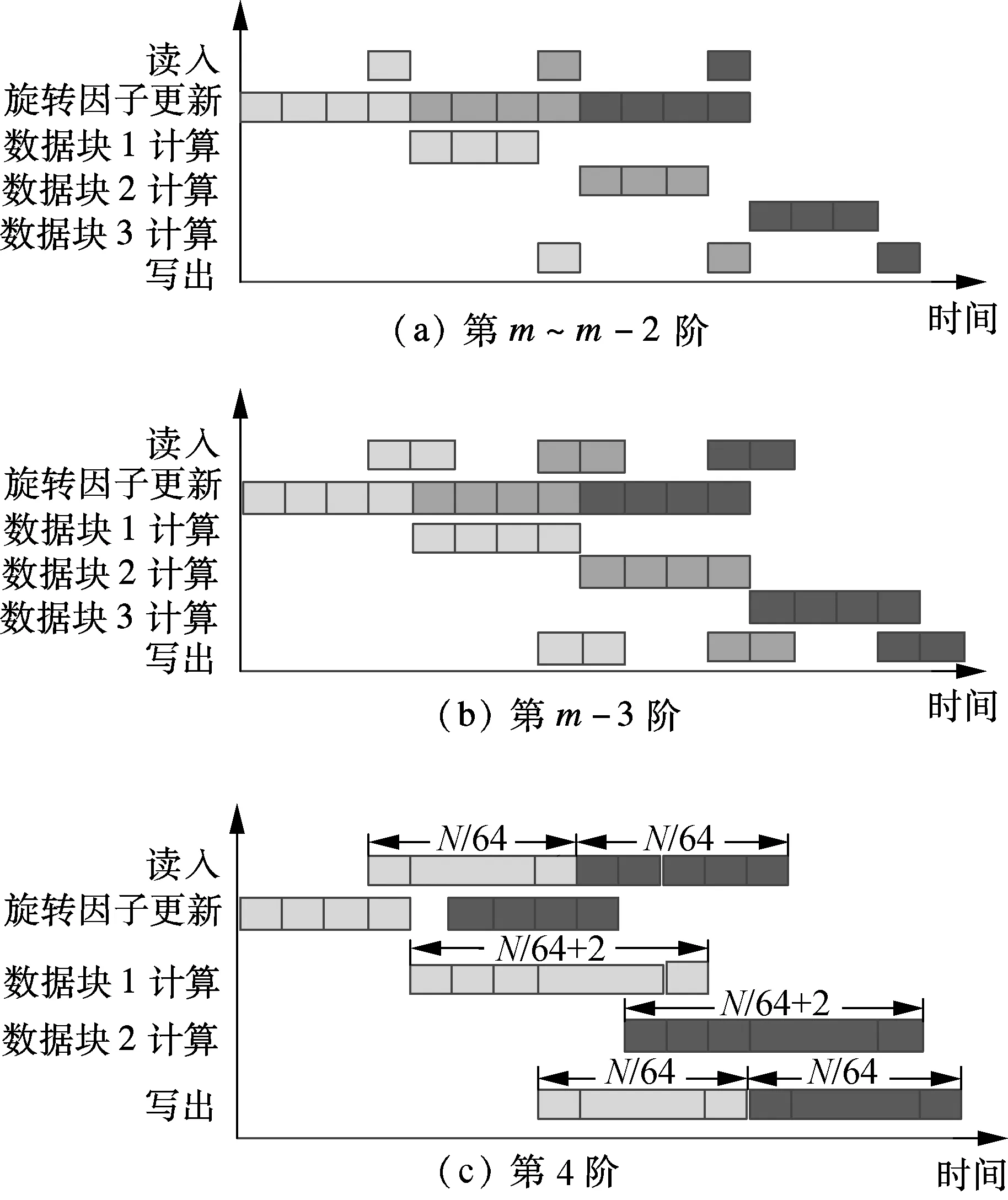
图6 FFT各阶计算的读入-计算-写出流水图

N点FFT运算的整体性能提升如图7所示,其中横坐标表示FFT的点数,纵坐标表示对应点数FFT的执行周期数T.通过采用流水气泡消除技术(优化1)和数据块重排技术(优化2),分别有效减少了Tcalc和Tdata-exchange,且收益随FFT点数的增加而增大.对于2 048点FFT运算,二者分别提升41.10%和7.47%的执行速度,整体执行速度提高了58.55%.

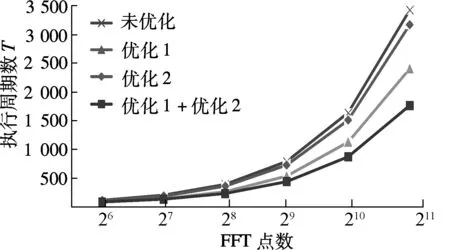
图7 N点FFT运算性能优化

本文基于REMUS_LPP实现了一款面向移动智能终端的SoC芯片.该芯片采用TSMC 65 nm LP工艺,工作频率为200 MHz,管芯照片如图8所示.该芯片面积为38.44 mm2,其中REMUS_LPP的面积为21.6 mm2.

图8 SoC芯片管芯照片

3.2 比较

将本文FFT算法实现的性能与其他同类并行计算平台实现结果进行了对比,包括NoC[7],MorphoSys[8],ePUMA[10]和SmartCell[9].平台硬件实现对比如表1所示.由表可见,REMUS_LPP片上存储需求仅为SmartCell[9]和MorphoSys[8]的28.1%和7.0%.

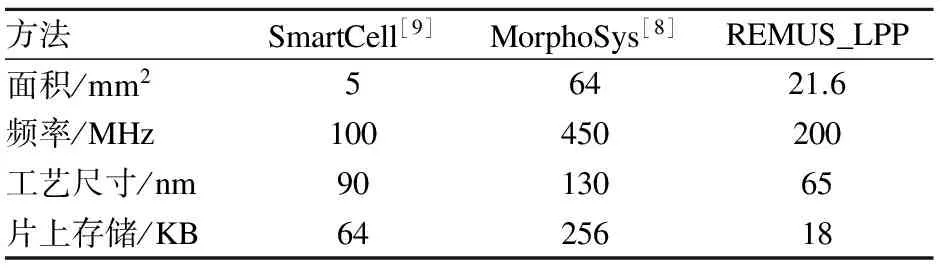
表1 并行架构与REMUS_LPP的硬件参数对比

FFT算法在不同平台上的性能比较如图9所示.在多种点数计算场景下,基于REMUS_LPP实现的FFT算法的性能提升至其他平台的2.15～13.60倍.

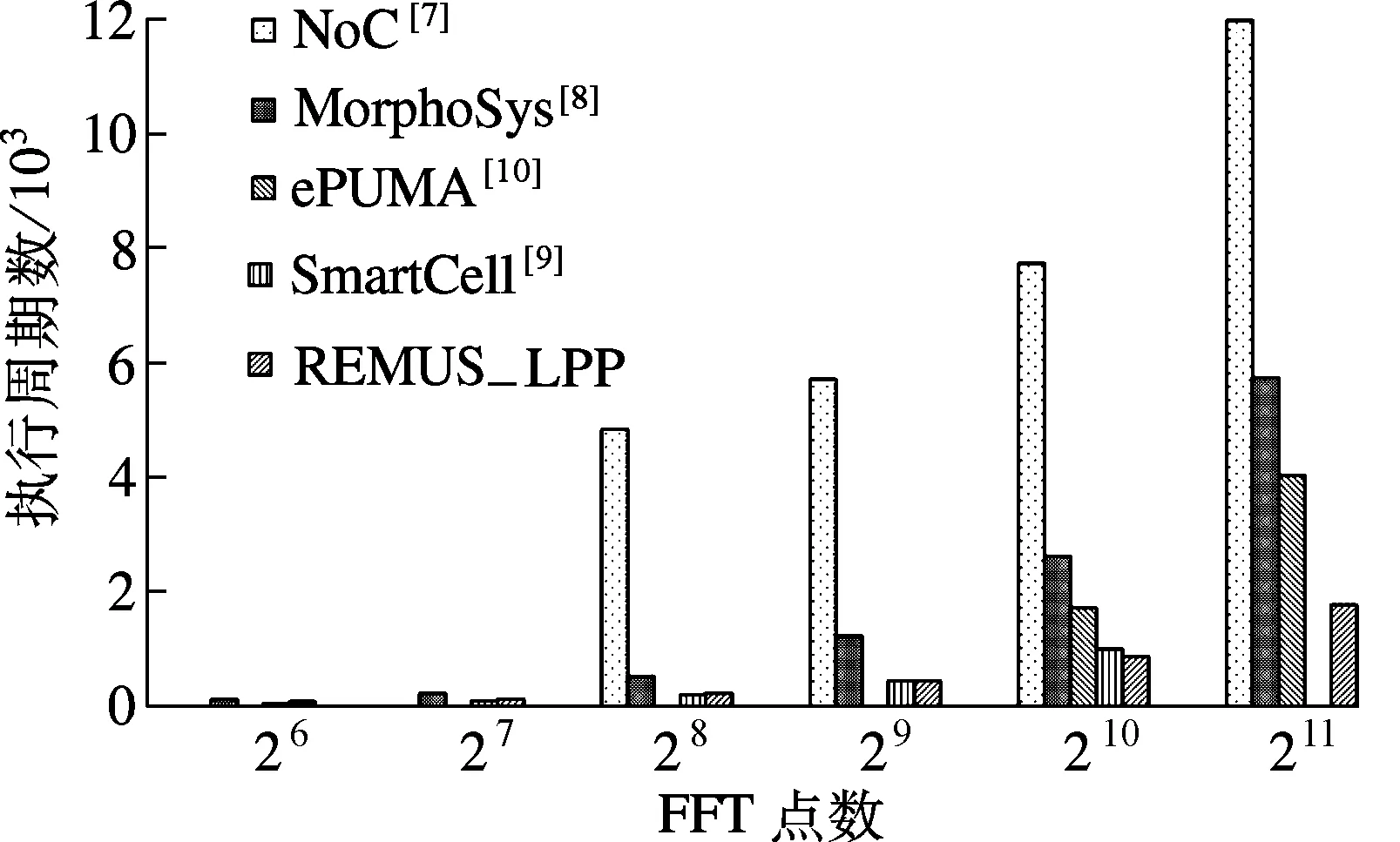
图9 FFT算法在不同平台上的性能比较

4 结语

本文基于粗粒度可重构架构REMUS_LPP提出了一种复数FFT并行化实现方案,通过引入流水线消除和数据块重排技术优化了性能.本文实现方案的执行速度提升至其他同类并行计算架构的2.15～13.60倍,而片上存储开销的需求仅为其他方法的7.0%～28.1%.

)

[1] Cervero T, López S, Callicó G M, et al. Survey of reconfigurable architectures for multimedia applications[C]//SPIEProceedingsofVLSICircuitsandSystemsⅣ. Dresden, Germany, 2009: 736303-01-736303-12.

[2] Hartenstein R. A decade of reconfigurable computing: a visionary retrospective [C]//ProceedingsoftheConferenceonDesign,AutomationandTest. Munich, Germany, 2001: 642-649.

[3] PACT Inc. White paper of reconfiguration on XPP-Ⅲ processor[R]. Munich, Germany: PACT Inc, 2006.

[4] Palkovic M, Cappelle H, Glassee M, et al. Mapping of 40 MHz MIMO SDM-OFDM baseband processing on multi-processor SDR platform [C]//11thIEEEWorkshoponDesignandDiagnosticsofElectronicCircuitsandSystem. Bratislava, Czechoslovakia, 2008: 86-91.

[5] Mei B, Sutter B, Aa T, et al. Implementation of a coarse-grained reconfigurable media processor for AVC decoder [J].JournalofSignalProcessingSystems, 2008,51(1): 225-243.

[6] Mei B, Veredas F J, Masschelein B. Mapping an H.264/AVC decoder onto the ADRES reconfigurable architecture [C]//InternationalConferenceonFieldProgrammableLogicandApplications. Tampere, Finland, 2005: 622-625.

[7] Bahn J H, Yang J S, Bagherzadeh N. Parallel FFT algorithms on network-on-chips [C]//FifthInternationalConferenceonInformationTechnology:NewGenerations. Las Vegas, NV, USA, 2008: 1087-1093.

[8] Kamalizad A H, Pan C, Bagherzadeh N. Fast parallel FFT on a reconfigurable computation platform [C]//15thSymposiumonComputerArchitectureandHighPerformanceComputing. St Paul’s, Brazil, 2003: 254-259.

[9] Cao L, Huang X M. Mapping parallel FFT algorithm onto SmartCell coarse-grained reconfigurable architecture [J].IEICETransactionsonElectronics, 2010,E93C(3): 407-415.

[10] Liu Z Y, Xie Q F, Wang H K, et al. A high performance implementation of non-power-of-two FFT with EPUMA platform[C]//InternationalWorkshoponInformationandElectronicsEngineering. Harbin, China, 2012,29: 3408-3412.

[11] Nguyen K, Cao P, Wang X X, et al. Implementation of H.264/AVC encoder on coarse-grained dynamically reconfigurable computing system [C]//FourthInternationalConferenceonCommunicationsandElectronics. Hue, Vietnam, 2012: 483-488.

[12] Liu B, Cao P, Zhu M, et al. Reconfiguration process optimization of dynamically coarse grain reconfigurable architecture for multimedia applications [J].IEICETransactionsonInformationandSystems, 2012,E95D(7): 1858-1871.

[13] Xiao J, Zhang J G, Zhu M, et al. Fast AdaBoost-based face detection system on a dynamically coarse grain reconfigurable architecture [J].IEICETransactionsonInformationandSystems, 2012,E95D(2): 392-402.

[14] Cooley J W, Tukey J W. An algorithm for the machine calculation of complex Fourier series [J].MathematicsofComputation, 1965,19(90): 297-301.