基于因子分析和贝叶斯估计的机床热误差建模*
2013-12-23代贵松杨建国朱小龙
代贵松,杨建国,朱小龙
(上海交通大学 机械与动力工程学院,上海 200240)
0 引言
随着科学技术的日新月异,制造业对于机床精度的要求不断提高[1]。大量研究表明,在高精、高速加工过程中,机床热变形引起的热误差占总误差的70%[2]。因此,机床热误差补偿能够很有效地提高机床的加工精度。在热误差补偿过程中,温度测点的布置、选择和热误差模型的建立是难点[3]。从经济上考虑,需要尽可能地减少传感器的数目,但太少的传感器势必影响热误差模型的精度[4]。因此,对温度测点进行优化布置,确定传感器的最优数目和最佳位置具有重要的实用价值。
本文采用因子分析对机床的温度变量进行分组[5],再从各分组中选择出与热变形相关系数最大的温度变量作为建模的典型变量,以减小温度变量之间的耦合性对于建模精度的影响,从而提高热模型的鲁棒性[6]。最后,根据优选出的典型温度变量,采用因子分析和贝叶斯估计建立机床热误差模型。结果表明,该方法大大提高了热误差模型的精度和鲁棒性,实现了热误差建模领域一次新的尝试,具有重大的理论意义和工程实践意义。
1 温度测点在机床上的优化布置
1.1 因子分析基本原理
因子分析是一种多变量统计分析方法[7],目的在于研究原始变量的内部关系,通过寻找变量的共同因子来简化和分析变量中存在的复杂关系。它把每个变量分解为两部分因子:一部分是由这些变量内含的公共因子构成,即所谓公共因子部分;另一部分是每个变量各自独有的因子,即所谓独特因子部分。从本质上来说,因子分析根据相关性的大小将变量分组,使得同组内的变量之间相关性较高,但不同组的变量相关性较低。由此可以认为,每组变量代表一个因子,它们可以反映问题的一个方面。
设F = (fij)= (f(1),…,f(k))为一个n × k 阶矩阵,U=(u(1),…,u(p))为一个n×p 阶矩阵,Λ=(λij)为k ×p 阶矩阵,且满足X =FΛ +U,写成向量表达式,有:
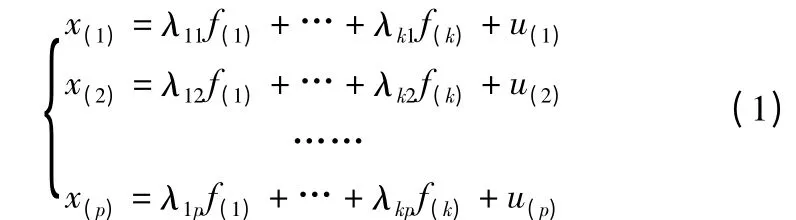
上式即为因子分析的数学模型,式中:k <p,f(1),f(2),…,f(k)为公共因子,u(1),u(2),…,u(p)为独特因子,λij表示第i 个变量x(i)在第j 个因子f(j)上的载荷。
1.2 利用因子分析选择关键温度变量
为了检测机床的温度场,按图1 所示,在一台车削中心上安装了16 个温度传感器,可分为五组:①两个传感器(0 和1)用于测量主轴箱的温度;②四个传感器(2 ~5)用于测量丝杆螺母的温度;③两个传感器(6 和7)用于测量冷却液温度;④一个传感器(8)用于测量室温;⑤七个传感器(9 ~15)用于测量床身温度。
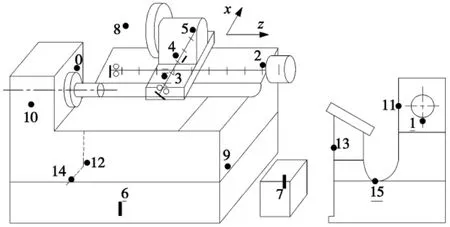
图1 温度传感器的布置
考虑到本文的篇幅,以主轴径向为例,采用数字式位移传感器测量主轴X 方向热漂移误差,位移传感器固定在刀架上,其布置如图2 所示。

图2 位移传感器在主轴径向的布置
定义编号为i 的温度传感器所测得的温度变量为Ti,位移传感器测得的位移误差为δ。在检测过程中,每隔450s 采集一次实验数据,共测得71 组数据,根据实验结果得到的机床主轴径向热误差和温度变化曲线如图3、图4 所示。
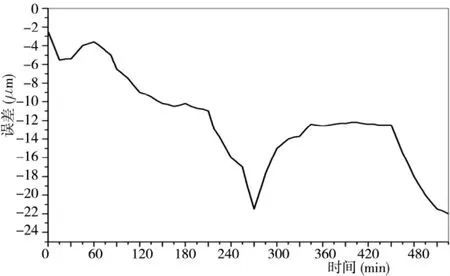
图3 机床主轴径向热误差曲线
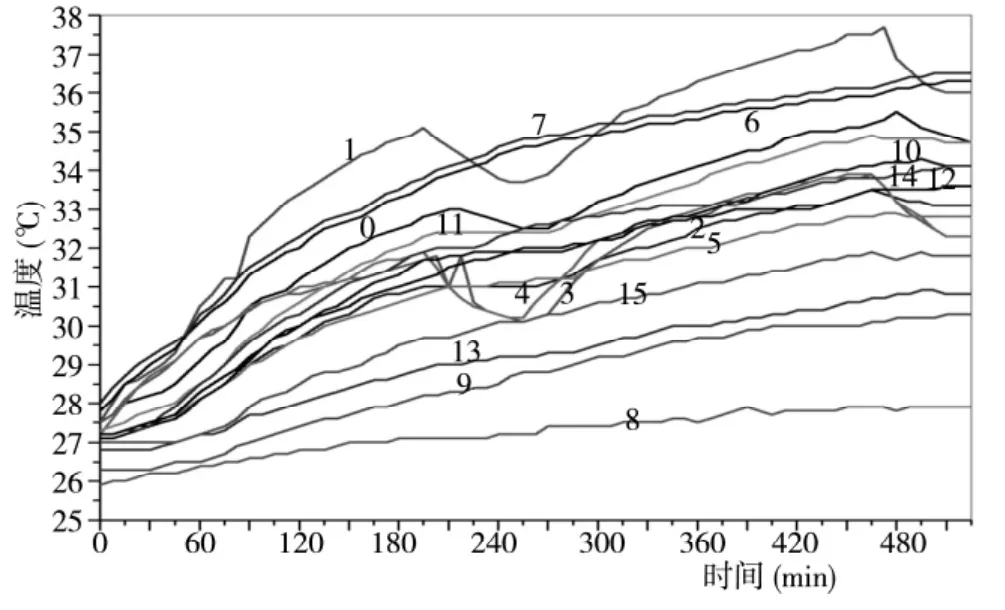
图4 机床温度曲线
对16 个温度变量进行因子分析:第一步计算出16 个温度变量的相关系数矩阵R;第二步利用雅克比方法计算出矩阵R 的特征向量和特征值;第三步计算各因子对总变差的贡献率和累计贡献率;第四步计算温度变量在各主因子上的载荷。根据上述步骤可获得前四个因子的特征值、贡献率、累积贡献率,如表1 所示。前四个因子的累积贡献率为96.701%,故可采用4 因子模型。最后,计算各温度变量在这四个因子上的载荷,如表2 所示。
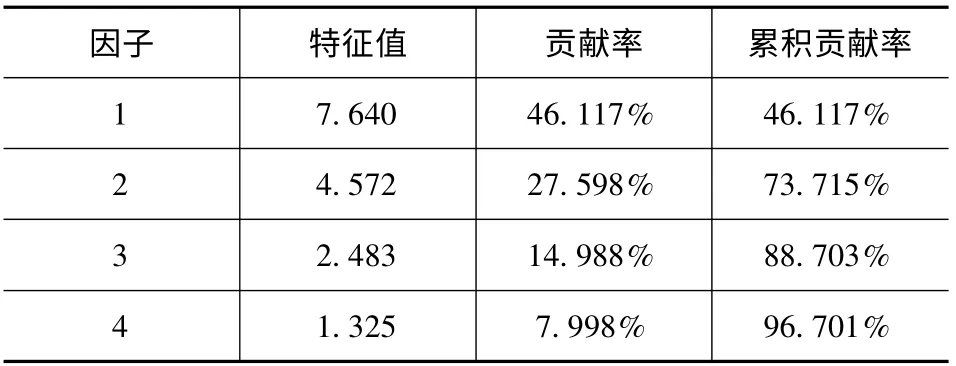
表1 总变差分解表
根据表2,将温度变量分为四组:选取在因子1上载荷较大的温度变量T3、T4、T6、T7、T10、T13、T15为第一组;选取在因子2 上载荷较大的温度变量T4、T6、T7、T9为第二组;选取在因子3 上载荷较大的温度变量T10、T15为第三组;选取在因子4 上载荷较大的温度变量T0、T1、T8为第四组。再根据各组温度变量与机床主轴热误差的相关系数大小,选择出丝杆螺母温度T4、冷却液温度T6、床身温度T15、主轴箱温度T1四个关键温度变量,该结果与文献[8]中通过灰色理论得到的温度关键点一致。

表2 载荷分布表
2 热误差建模
2.1 热误差模型推导
将机床径向热误差δ 与优选的四个关键温度变量T4、T6、T15、T1组成模型输入数据集X =[x0,x1,x2,x3,x4]=[δ,T4,T6,T15,T1],X 是n ×p 维矩阵。其中n=71,p=5,δ 为71 组热误差组成的列向量,Ti(i=4,6,15,1)为71 组温度值组成的列向量,由此可推导出机床的热误差模型。
首先,建立X 的因子分析模型,如下式:

式中,F 是X 的n×m 维主因子阵,Λ 是X 的m×p 维因子载荷阵,U 是X 的n×p 维特殊因子阵,m <5。
其次,对式(2)进行代数变换,两边同乘以C =Λ'(ΛΛ')-1可得:

令X0=x0,X1=[x1,x2,x3,x4],则X =[X0,X1];令C0为C 的第一行组成的行矩阵,C1为C 其余行构成的矩阵,则C=[C0,C1]T。
由此,式(3)可变为:

再次,对式(4)进行代数变换,两边同乘以C0'
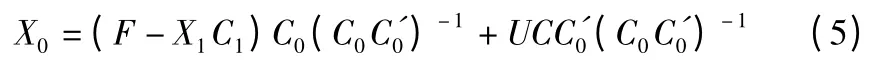
(C0C0')-1可得:即得到最终的机床热误差模型如下式:

在上式中,F、U、C 均是未知参数,本文采用贝叶斯估计的方法予以求出。
2.2 模型参数的贝叶斯估计
在因子分析模型(1)中,u(i)(i =1,2,…p)相互独立,且服从多元正态分布N(0,Ψ),Ψ 为p×p 维协方差阵,并由此可推知:
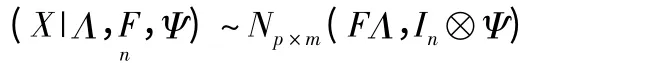

上式是因子分析模型的极大似然函数,下面讨论参数的贝叶斯估计问题[9]。
模型参数先验分布的设置是贝叶斯估计的基础,对于因子分析模型参数,Λ 的先验分布为矩阵正态分布,Ψ 的先验分布为Wishart 分布,F 的先验分布为矩阵正态分布,假设参数(Λ,Ψ)与F 相互独立,即:

其中,
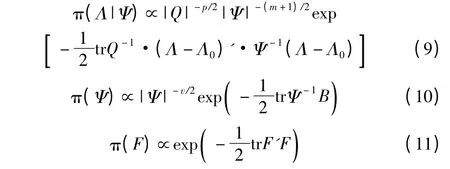
式中:B 是对称正定阵,H >0 为对称正定阵,(v,Q,B,Λ0)为超参数,具体设置方法见文献[10]。
模型参数后验估计采用最大后验估计(MAP),是通过模型参数的后验分布进行迭代得到的,因此要先计算模型参数的最大后验分布。
根据贝叶斯定理可推导出因子载荷阵Λ 的最大后验分布为:

在式(12)中,~Λ = (X'F + Λ0D-1)(D-1+ F'F)-1,显然当Λ =~Λ 时,π(Λ|F,Ψ,X)取最大,故Λ的最大后验估计是:
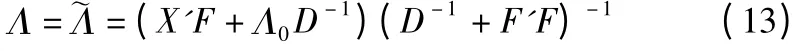
同理可得,Ψ 的最大后验估计是:

F 的最大后验估计是:
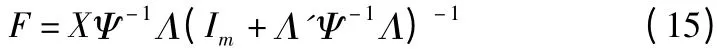
根据式(13)、(14)、(15),利用迭代法可以得到用于热误差模型的的参数估计,即

在式(16)、(17)、(18)中,k 的取值范围是0,1,…n,整个迭代过程持续到(Λk+1,Ψk+1,Fk+1)收敛为止。
综合式(2)、(16)可得:
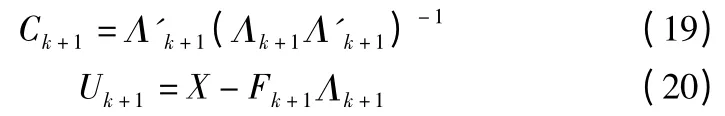
2.3 模型验证
机床主轴径向热误差δ 与四个关键温度变量T4、T6、T15、T1组成的数据集为模型输入,即2.1 所推导出的热误差预测模型,为模型1;机床径向热误差δ 与全温度变量T0、T1、…、T15组成的数据集为模型输入,按照2.1 中同样的方法,推导出类似的热误差预测模型,为模型2;以T4、T6、T15、T1为自变量,δ为因变量,采用最小二乘法得到机床的热误差模型,为模型3。模型3 的表达式为:

图5 为三个热误差预测模型对原始测量热误差的拟合情况。将模型预测热误差与原始测量误差做差值运算,可得到三个热误差预测模型的残差,如图6 所示。通过图5、图6 不难看出:对于原始测量热误差的拟合情况:模型1 比模型3 好,模型3 比模型2好;残差变化范围:模型1 比模型3 小,模型3 比模型2 小。综合比较,模型1 对热误差的预测结果最好。
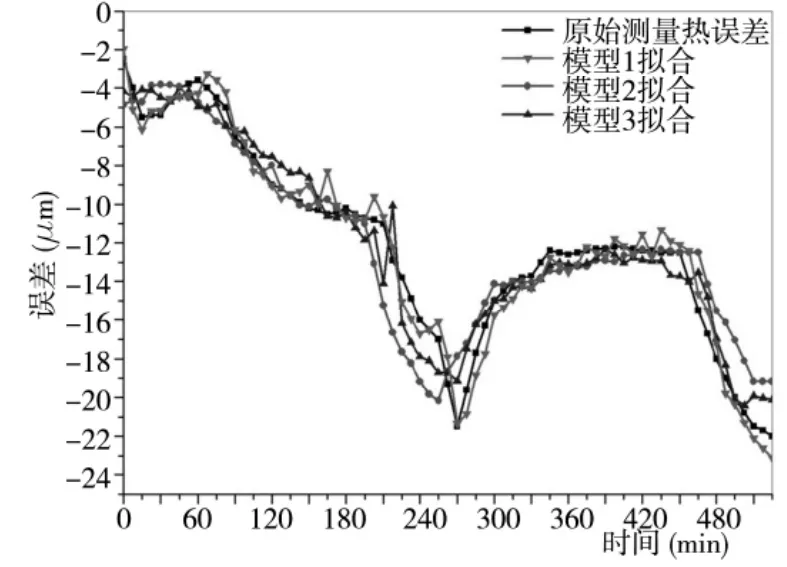
图5 预测模型的拟合情况

图6 预测模型的残差
通过因子分析和贝叶斯估计的建模补偿,使机床的径向热误差从22μm 减小到了4μm 以内,补偿效果达到了82%,大大提高了机床的加工精度。
3 结论
因子分析是较好的温度测点优化策略,极大地减少了传感器的数量,有效地避免了热误差模型中的耦合现象,提高了热误差的辨识精度。
通过因子分析模型推导出热误差预测模型,然后对模型中的参数进行贝叶斯估计,实验验证了这一方法可用于热误差建模,模型精度比最小二乘法高,而且鲁棒性也比最小二乘法好。
[1]W.S. Yun,S.K. Kim,D.W. Cho,Thermal error analys is for a CNC lathe feed drive system,International Journal of Machine Tools and Manufacture,1999(39):1087-1101.
[2]Zhao Haitao,Yang Jianguo,Shen Jinhua,Thermal error optimization modeling and real-time compensation on a CNC turning center. International Journal of Machine Tools and Manufacture,2007,207(2008):172-179.
[3]苏铁明,叶三排,孙伟. 基于FCM 聚类和RBF 神经网络的机床热误差补偿建模[J]. 组合机床与自动化加工技术,2011,2011(10):1-4.
[4]林伟青,傅建中. 数控机床热误差建模中的温度传感器优化研究[J]. 成组技术与生产现代化,2007,24(3):5-8.
[5]严乐,刘红忠,卢秉恒,等. 高精度压印机热误差补偿中温度变量的辨识[J]. 西安交通大学学报,2006,40(7):827-830.
[6]杨建国,薛秉源. CNC 车削中心热误差模态分析及鲁棒建模[J]. 中国机械工程,1998,9(5):31-35.
[7]张润楚. 多元统计分析[M]. 北京:科学出版社,2003.
[8]李永祥,童恒超,杨建国. 灰色系统理论在机床热误差测点优化中的应用[J]. 机械设计与研究,2006,22(3):78-80.
[9]吴喜之,科茨(Kotz,Samuel). 现代贝叶斯统计学[M].北京:中国统计出版社,2000.
[10]Liu Y-K and Liu B.Fuzzy Random Variables:A Scalar Expected Value Operator[J]. Fuzzy Optimization And Decision Making,2003,11(2):143-160.
