自然数的类杨辉三角性与循环性

刘 辉, 邓海云

(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)

1 引言和预备知识

数学大师陈景润、张明尧给出了一些自然数二次幂的独特性质:两位数(xy)102=(abcd)10((abc)10)，且(yx)102=(dcba)10((cba)10)，三位数性质类似,并找出了具有这一性质的所有两位、三位数.本文在此基础上首先对二次幂的性质作进一步的完善,同时给出两个相应定义;其次研究两位数三次幂的相应性质,并对具有这一性质的两位数给出证明.有关自然数的独特性质可参见文献[1-6].

定义1若两位数(xy)102=(abcd)10((abc)10),且(yx)102=(dcba)10((cba)10)，则称自然数(xy)10具有2-循环性.

定义2若两位数(xy)10n=(ab…pq)10，且(yx)10n=(qp…ba)10,则称自然数(xy)10具有n-循环性,简称循环性.

定义3若两位数(xy)102=(abcd)10((abc)10)满足(x+y)2=a+b+c+d(a+b+c),则称自然数(xy)10具有2-类杨辉三角性.若(xy)10对三次幂具有这一性质,则称(xy)10具有3-类杨辉三角性,简称类杨辉三角性.

以上3个定义可以推广到三位数及更高次幂.

定理1若自然数(xy)10具有类杨辉三角性,则它必具有循环性,即对一个自然数(xy)10而言，类杨辉三角性是循环性的充分条件.

证明假设以2次幂为例,自然数(xy)10若具有类杨辉三角性,即(xy)102=(abcd)10((abc)10)满足(x+y)2=a+b+c+d(a+b+c),通过计算发现,112=121,又(1+1)2=1+2+1,则自然数11具有2-循环性.依次试下去,可得下列两位数具有类杨辉三角性的性质:

112=121,112=121,(1+1)2=1+2+1;

122=144,212=441,(1+2)2=1+4+4;

132=169,312=961,(1+3)2=1+6+9;

222=484,222=484,(2+2)2=4+8+4.

则自然数(xy)10具有2-循环性.同时我们发现152=225,而512≠522;552=3025,而3025≠5203,所以这两个自然数不满足类杨辉三角性,故也不满足循环性.同理可得高次幂也具有该性质.则自然数(xy)10具有循环性.

2 两位、三位数的2-循环性和2-类杨辉三角性

2.1 两位数的循环性和类杨辉三角性

性质1所有具有类杨辉三角性的两位数为：11,12,13,22.

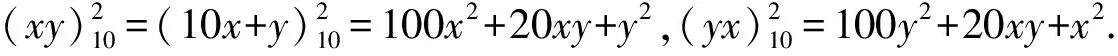
先固定其中一个,即x=1,就有(1y)2=100+20y+y2,(y1)2=100y2+20y+1.(1y)2的最大值小于400,于是1≤y≤3,否则它的平方数达到四位数,不符合要求.即当x=1时,具有这种性质的二位数只能从以下数字中找：11,12,13，但是它们都符合要求.

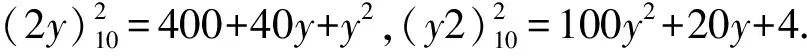
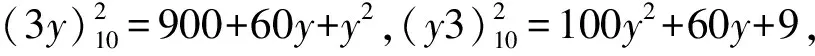
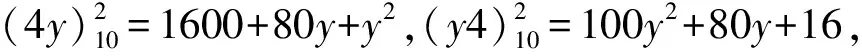
若x=5,…,9，可证明其具有类似的情况.因此,只有11,12,13,21,22,31这6个两位数满足上述性质.

2.2 三位数的循环性和类杨辉三角性

定理2若三位自然数具有循环性,当且仅当它具有类杨辉三角性.

证明对于三位数与二位数讨论方法一样,(xyz)10表示三位数,x,y,z分别表示百十及个位数字.为了使(xyz)10具有上述性质,则必须满足1≤x≤9,0≤y≤9,1≤z≤9.

在这里我们只讨论x=1的情况,则有:

(1yz)102=(100+10y+z)2=10000+100y2+

2000y+20yz+z2

(1)

(zy1)102=(100z+10y+1)2=10000z2+

2000yz+100y2+20y+1

(2)

由式( 2 )可知,(zy1)102的个位数为1,由于10000<(1yz)102≤39601,故(1yzx)102是一个五位数.对0≤y≤3有(1yz)102≤1392=19321,对y≥5有(1yz)102>1502=22500,而y=4时,对z=1有(1yz)102=1412=19881,对2≤z≤9有20164=1422≤(1yz)102≤1492=22201.因此必须有

0≤y≤3,1≤z≤9或y=4,z=1

(i)

又若z≥4,则(zy1)102≥4012=160801,这是一个六位数,而(1yz)102<2002=40000,这是一个五位数,因此必须有

0≤y≤3,1≤z≤3或y=4,z=1.

(ii)

而对y=3,则有

(1yz)102=(13z)102=16900+260z+z2

(3)

(zy1)102=(z31)102=10000z2+6200z+961

(4)

当z=3时,式(3)的个位数为9,而式(4)的最高位数为1,显然不符合条件,则必须有

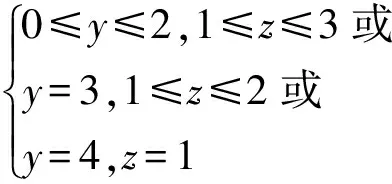
(iii)

要满足( iii),则只有在下列数中寻找:

101,102,103,111,112,113,121,122,123,131,132,141.

经计算,当y=0时,z=1,2,3都满足上面的性质;当y=1时,z=1,2,3时满足上面的性质;当y=2时,z=1,2满足上面的性质.其余的三位数依此类推.综上所知,仅以下15个数满足要求，即101,102,103,111,112,113, 121,122, 201, 202,211,212，221,301,311.还可以对更高位数进行讨论,这里不再说明.

通过2.1及2.2的证明说明,满足循环性的自然数必定满足类杨辉三角性,则给出如下定理.

3 两位数的3-循环性和3-类杨辉三角性

上面已经给出了所有满足2-循环性和2-类杨辉三角性的两位自然数,那么现在将这两个性质推广到3-循环性和3-类杨辉三角性.

性质2所有具有3-类杨辉三角性的两位数为:11.

证明记(xy)10表示一个两位数，为使其满足2-循环性和2-类杨辉三角性,显然x=0或y=0不成立,于是必须有1≤x≤9,1≤y≤9.

1)当y=1时,有

(x1)103=(10x+1)3=(100x2+20x+1)×

(10x+1)=1000x3+300x2+30x+1

(5)

(1x)103=(10+x)3=(100+20x+x2)×

(10+x)=1000+300x+30x2+x3

(6)

于是,由式(5)得(x1)103的个位数为1,若(x1)10要满足上述性质,则(1x)103的最高位数必须为1,而1331≤(1x)103<8000,并且它只是一个四位数,而2≤x≤9时,最高位数均不为1,即只有11满足.

2)当y=2时,有

(x2)103=(10x+2)3=(100x2+40x+4)×

(10x+2)=1000x3+600x2+120x+8

(7)

(2x)103=(20+x)3=(400+40x+x2)×

(20+x)=8000+1200x+60x2+x3

(8)

于是,由式(7)得(x2)103的个位数为8,若需满足上述性质，则(2x)103的最高位必须为8,而9261≤(2x)103≤23489,则(x2)10显然不满足.

3)当y=3时,有

(x3)103=(10x+3)3=(100x2+60x+9)×

(10x+2)=1000x3+900x2+270x+27

(9)

(3x)103=(30+x)3=(900+60x+x2)×

(30+x)=27000+2700x+90x2+x3

(10)

于是,由式(9)得(x3)103的个位数为7,而29791≤(3x)103≤59319,则(x3)10显然不满足.

4)当y=4时,有

(x4)103=(10x+4)3=(100x2+80x+16)×

(10x+4)=1000x3+1200x2+480x+64

(11)

而68921≤(4x)103≤117649,则(x4)10显然不满足.

5)当y=5时,(x5)103的个位数为5,而132651≤(5x)103≤205379,则(x5)10显然不满足.

6)当y=6时,(x6)103的个位数为6,而226981≤(6x)103≤328509,则(x6)10显然不满足.

7)当y=7时,(x7)103的个位数为3,所以(7x)103的最高位必须为3,而357911≤(7x)103≤493039,因为743=405224,故只能在71,72,73中找,由1),2),3)的讨论可知，71,72,73均不满足,则(x7)10不满足.

8)当y=8时,(x8)103的个位数为2,而531441≤(8x)103≤704969,则(x8)10显然不满足.

9)当y=9时,(x9)103的个位数为9,而753571≤(9x)103≤970299,通过计算只有973,983,993三个数的最高位数为9,经计算均不满足,则(x9)10也不满足.

综合1)～9)可知,所有具有3-类杨辉三角性的两位数为11.

4 结束语

经过计算还发现:1113=1367631,(1+1+1)3=1+3+6+7+6+3+1=27;1013=1030301,(1+0+1)3=1+3+3+1.114=14641,(1+1)4=1+4+6+4+1;1014=104060401,(1+0+1)4=1+4+6+4+1;经过计算1114不满足类杨辉三角性,再考虑11,101的五次幂也不再满足.通过上述两位数,三位数的二次、三次幂的证明可知，随着位数及次幂的增大,满足循环性和类杨辉三角性的自然数越来越少,那么是否可以断定到了一定的p位数及q次幂后就不会出现自然数满足上述性质,这有待于我们进一步的研究.

[1]陈景润,张明尧.关于自然数中的一些有趣的性质[J].中学数学杂志,1985(8)：2-4.

[2]吴维煊.由杨辉三角形构建的数学联系[J].数学教学研究,2010,29(2):54-57.

[3]王进明.初等数论[M].北京:人民教育出版社,2002.

[4]朱伟义.有关自然数方幂和公式系数的一个新的递推[J].数学的实践与认识,2004,34(10):170-173.

[5]赵新华.自然数幂和公式的对称形式[J].云南民族大学学报：自然科学版,2011,20(6):481-485.

[6]孟凡申.自然数幂方和用二项系数表示的系数公式[J].数学的实践与认识,2010,40(20):159-166.