基于GPS的土地面积测量算法

王陈陈， 马明建， 马娜， 张文道， 申瑞霞

(1.山东理工大学 农业工程与食品科学学院, 山东 淄博 255091；2.山东科技职业学院 经济管理系, 山东 潍坊 261053)

面积测量对于精细农业、林地测量、土地勘察等都是非常重要的.GPS作为一种方便快捷的测量手段，已经广泛应用于生产实践和社会发展.本系统从GPS接收机中实时采集NEMA-0183语句，从语句中提取经度、纬度、速度等有用信息并存储，根据测量信息计算规则土地区域和不规则土地区域面积.

1 面积测量系统

1.1 面积测量系统组成

面积测量系统组成如图1所示.

图1系统组成图

测量系统软件界面如图2所示.

图2 测量系统软件界面图

1.2 高斯投影

从GPS语句中得到的经纬度数据是基于大地坐标系的位置数据，要通过高斯投影将大地坐标转化成高斯平面直角坐标.大地坐标记为(L，B)，高斯平面直角坐标记为(x，y)，则可以用式(1)表示.

从赤道开始到任意纬度的平行圈之间的弧长投影是高斯投影的关键步骤，采用积分法可以保证弧长投影的精度[1].弧长投影公式为

(2)

本系统使用以下公式进行高斯投影.

(3)

14η2-58η2t2)l″5

(4)

当l<3.5°时，式(3)、式(4)换算精度为0.001m.本系统选择3°带投影，以第20带的中央子午线117°为中心线进行投影，横坐标加500 000m.

1.3 解析法

本系统使用坐标解析法计算面积，该算法计算精度高，可作为面积的基本控制.坐标解析法假设有n个点 (X1，Y1)、(X2，Y2)、(X3，Y3),…,(Xn，Yn)、(Xn+1,Yn+1)，其中，Xn+1=X1，Yn+1=Y1.组成多边形的点按逆时针排列，则该多边形的面积为

(5)

计算周长则使用以下公式

(6)

2 单点定位精度

单点定位精度是土地面积测量的基础.本系统使用多次定位取平均值法和拉依达准则提高单点定位精度.

2.1 接收机定位误差

由于GPS接收机自身固有的坐标数据误差，以及在测量过程中建筑物、天气等因素对GPS接收机的干扰，GPS接收机输出数据是跳动的，往往存在异常值[2].本系统从GPS接收机指示灯闪烁开始，采集输出定位数据，如图3所示.

GPS接收机输出的纬度、经度数据如图4、图5所示.

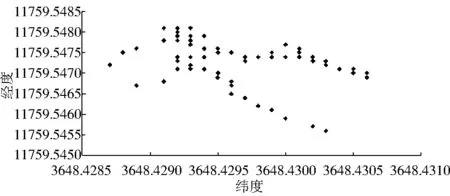
图3 系统采集到的定位数据

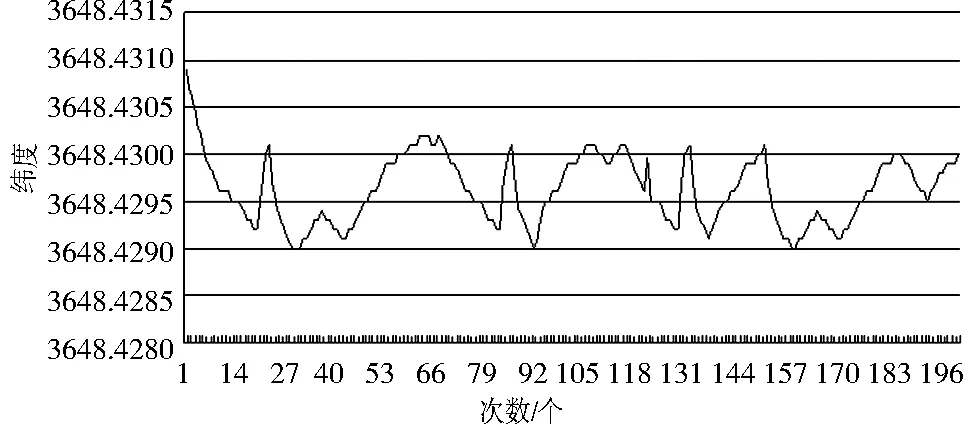
图4 纬度坐标数据

由图4、图5可知，GPS接收机在开机一定时间后，输出定位数据在一定的稳态区间内震荡.实际上，GPS接收机的最终输出值是在一定误差半径内震荡的.

2.2 拉依达准则剔除异常值

(7)

采用拉依达准则处理图3定位数据，处理结果如图6所示.

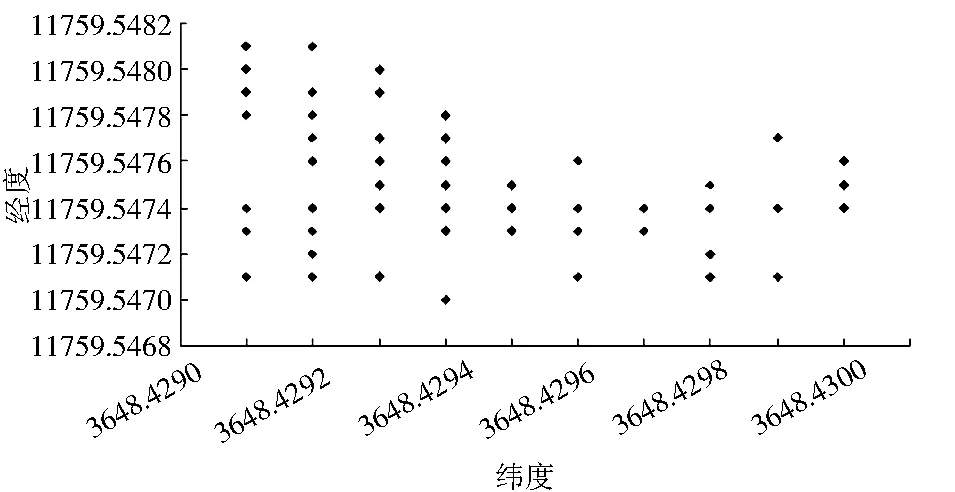
图6 拉依达准则处理后的定位数据

由图6可知，经拉依达准则处理后，剔除了稳态区间外的异常值，缩小了定位误差.

2.3 多次定位取平均值

用拉依达准则处理后的数据处于一定稳态区间内.本系统采用算术平均法对稳态区间内数据做数字滤波处理，确定单点定位值.假设对某一量进行n次等精度测量，其测量值为X1、X2、…、Xn，则其算术平均值表示为

(8)

理论上，n值越大，最终值越接近实际值.但这并不意味着观测次数n越大越好.为确定合理的测量次数n，本系统进行了6组试验.用GPS接收机采集6组数据，首先用拉依达准则剔除异常值，优化样本数据，再计算X坐标和Y坐标的标准方差和误差半径e，表1为试验结果.

图7为测量次数n与误差半径关系图.

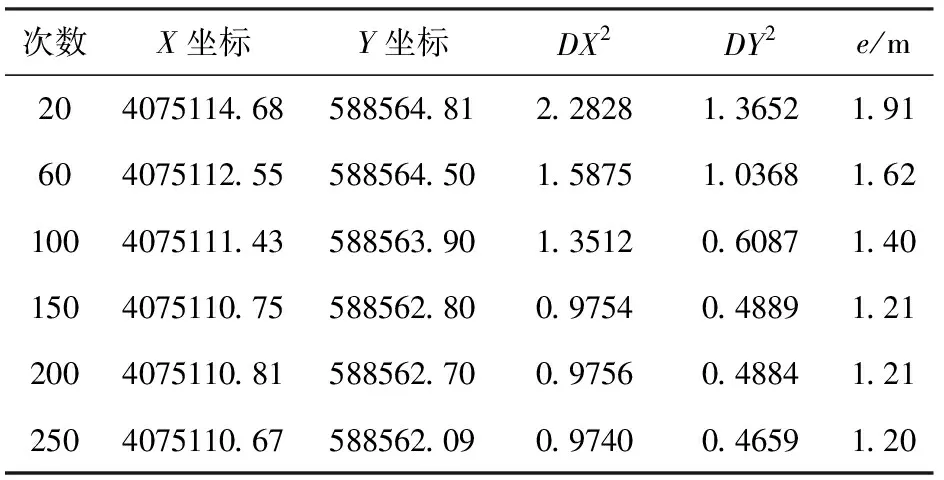
表1 测量次数n与单点定位精度分析

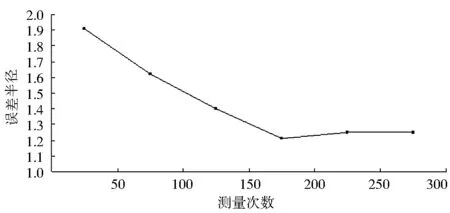
图7 测量次数n与误差半径关系

由表1可知，当n=20～150，测量次数n与精度递增关系明显，当n=150～250，精度递增不明显.因此，对于单点定位，考虑时间成本和精度两方面因素，本系统确定测量次数为n=200，以其测量结果的算术平均值作为测量点的实际坐标值.

3 面积测量试验

土地面积测量可分成规则土地区域和不规则土地区域两种情况进行试验.

本文中规则土地区域指的是边界之间有明显转折点的规则多边形地块，一般有航线法和航迹法两种测量方法[4].航线法是在边界转折点取定位数据，根据有限个点组成多边形，用解析法计算该多边形面积.航迹法是绕待测区域边界行进，获得一系列界址点的坐标信息，根据界址点计算面积.

不规则土地区域指不规则多边形土地区域.求积仪法可获得较高精度不规则土地面积，但不适用于野外作业.航迹法简单有效，而且测量面积越大，精度越高.国内外有提出插值法，即在曲线上测定若干界址点位置，再进行曲线内插，然后利用测定点和内插点计算任意图形面积[5].但如果差值次数过高，增加计算量.分段内插、低次内插的精度要比不分段内插、高次内插的精度高[6].因此本文采用分段二次内插法进行不规则土地面积测量.

3.1 规则地块区域试验

本系统试验对象为一块方型地块，用皮卷尺测得该方型地块为长134m，宽83m的长方形，面积为11 122m2.采用前面叙述的单点定位方法，使用GPS接收机取得该方型地块四个边界转折点的坐标数据为(x1，y1)、(x2，y2)、(x3，y3)、(x4，y4)，代入式(5)、式(6)求得航线法测量方型地块的面积.

然后手持GPS接收机和笔记本电脑，匀速笔直地沿方型地块边界逆时针环绕一圈，采集界址点坐标，共采集到320个点，代入式(5)、式(6)即完成了航迹法测量方型地块面积计算.表2为采用航线法和航迹法得到的测量结果比较.

表2 航线法和航迹法测量结果比较

从表2可知，对于边界明显的规则土地区域，尽管航线法的测量点数少于航迹法，但具有更好的测量结果，其测量结果更接近实际值.

3.2 不规则地块区域试验

本系统以400m田径操场作为试验对象，首先采用几何图形计算法对田径操场进行量算，几何图形计算法是将面积图形分割成若干简单图形，实测几何图形的边长和角度，此法精度较高，但较复杂且不方便.基于此法的量测结果面积为S=10 715m2.环绕田径操场一周，采集边界界址点坐标信息，用航迹法计算得出面积数据.然后再用插值法对操场两端的曲线部分进行计算.插值法的原理是在曲线上均匀地测量几个界址点，然后利用这几个界址点进行曲线的拟合，求出能代表该曲线的插值函数f(x)，计算任一点xi的函数值f(xi)，此f(xi)就成为原函数在xi处的插值.选取曲线两端和曲线中点三个位置的GPS定位数据：(3648.8614，11759.3348)、(3648.8814，11759.3134)、(3648.8669，11759.2845)，将这三个点进行高斯投影，转化成平面坐标值(4075909.28，588238.47)、(4075946.53，588206.08)、(4075919.53，588163.48)，为计算方便，x坐标减去4075900，y坐标减去588100，简化后的三点坐标值为(9.3，138.5)、(46.5，106.1)、(19.5，63.5).图8为插值点图.

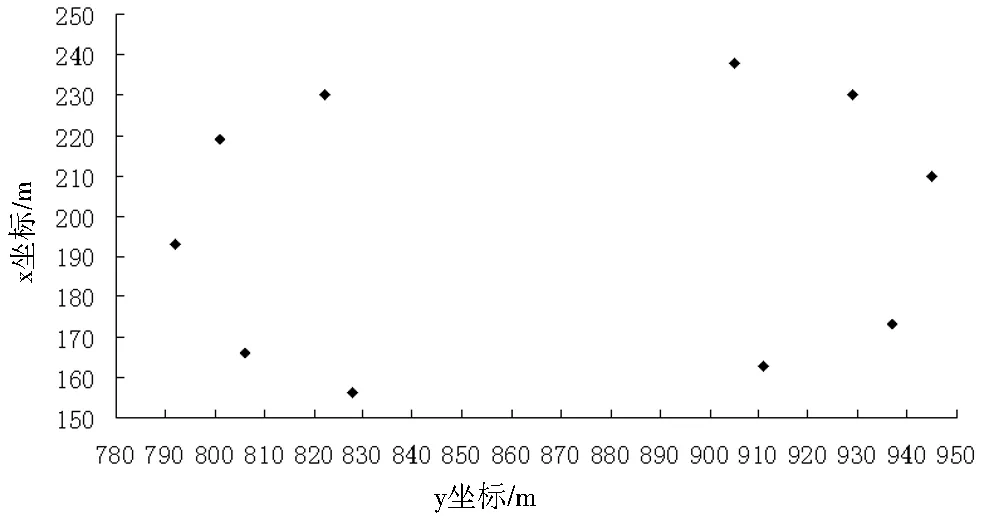
图8 插值点图

代入二次内插公式得

解式(9)得到一个二次多项式

y=0.03x2-8.4x+216.1 (10)

将此二次多项式作为计算田径操场弧段的内插函数.采用分段内插法，参考《地籍测量学》一书中计算椭圆部分面积的方法，每两点之间内插五个点，利用这13个点组成的多边形，解析法计算面积，得到S1=3 736m2，然后计算两端直线的长度以及中间长方形场地的面积.两端直道面积S2=6 765m2.相加得到操场的总面积S=10 501m2.航迹法与插值法的计算数据如表3所示.

表3 航迹法与插值法计算操场面积

从表3可知，在测量曲线边界的区域时，插值法的测量结果比航迹法更准确.

4 试验结论

根据上述试验可以得出以下结论：

1)采用多次测量取平均值法，并用拉依达准则剔除异常值，可以显著提高土地勘探中GPS单点静态定位精度；而且测量次数n=200时，测量结果的算术平均值可作为最终值.

2)当测量对象为规则地形区域时，应采用简单省时的航线测量法，该法比航迹法的测量结果准确，面积相对误差率为4.6%.

3)当测量对象为不规则地形区域时，采用分段二次多项式内插法，可以有效地减小测量误差，面积相对误差率为2.0%.

[1]刘正才.子午线弧长公式的简化及通用高斯投影计算程序介绍[J].测绘工程，2001，10(1):55-56.

[2]任婷，曲国庆，张华荣，等.基于小波相关性的对流层延迟改正数据分析[J].山东理工大学学报：自然科学版，2012，26(4):25-29.

[3]赵进文.异常值对计量建模影响的典型案例[J].统计研究，2010，27(12):92-98.

[4]高建东，雷郁文.利用后差分技术提高手持GPS的定位精度[J].物探与化探，2006，30(5):446-449.

[5]章书寿，孙在宏.地籍测量学[M].(修订版).南京：河海大学出版社，2004：106-108.

[6]杨丽萍，王宏勇.分形插值函数及其分数阶积分的扰动误差估计[J].山东理工大学学报：自然科学版，2011，25(5):16-18.