具有时滞的p－Laplacian方程非局部问题迭代正解的存在性

郑春华 ，刘文斌

(1.陕西工业职业技术学院基础部，陕西咸阳712000;2.中国矿业大学数学系，江苏徐州221116)

在人口理论、医学、生物等领域中应用时滞微分方程，具有丰富的实际背景和重要的应用价值，一直受到人们的广泛关注.近年来，时滞微分方程的边值问题研究获得了一些重要的结果［1－5］，这些结果主要集中在时滞微分方程的周期边值问题和两点边值问题上.虽然常微分方程的多点边值问题已取得不少结果［6－8］，但对于时滞微分方程的非局部边值问题的研究结果还不是很多. 文献［9］利用Guo－Krasnoselskii 不动点定理研究了边值问题

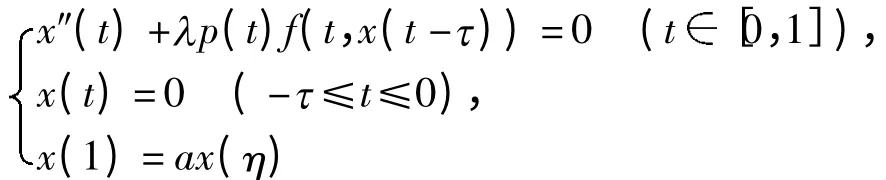
正解的存在性.

文献［10］用同样的工具研究了问题

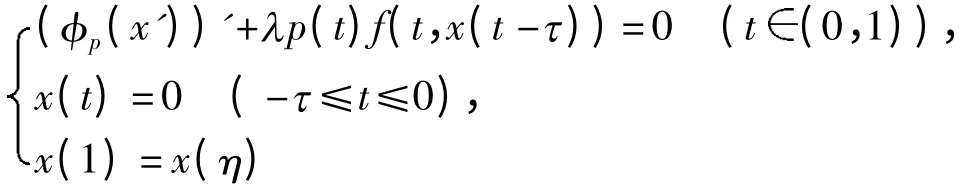
正解的存在性.

受以上研究工作的启发，本文利用单调迭代方法研究具有时滞的p－Laplacian 方程非局部边值问题

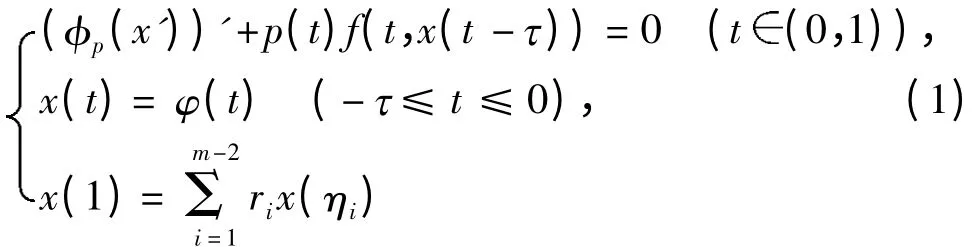
正解的存在性，得到了边值问题(1)存在正解的充分条件，并确立了收敛到该正解的迭代序列，其中为常数，m 为大于2的整数.

本文始终假设以下条件成立.

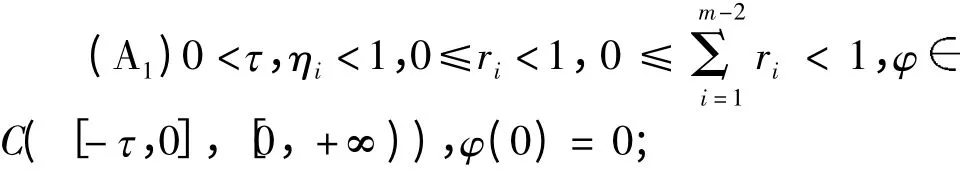
(A2)p(t)是定义在(0，1)内的非负可测函数且在(0，1)的任何子区间内不恒等于零;

(A3)fC(［0，1］×［0，+∞)，［0，+∞)).

1 预备知识

令

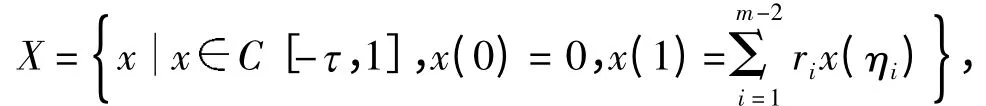
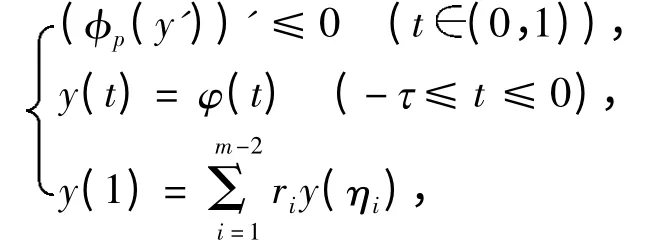
证明 利用(φp(y'))'≤0 和φp的单调性及条件(A1)易知引理1 结论成立.

定义算子T:X→X

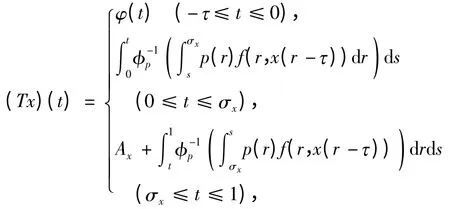
这里

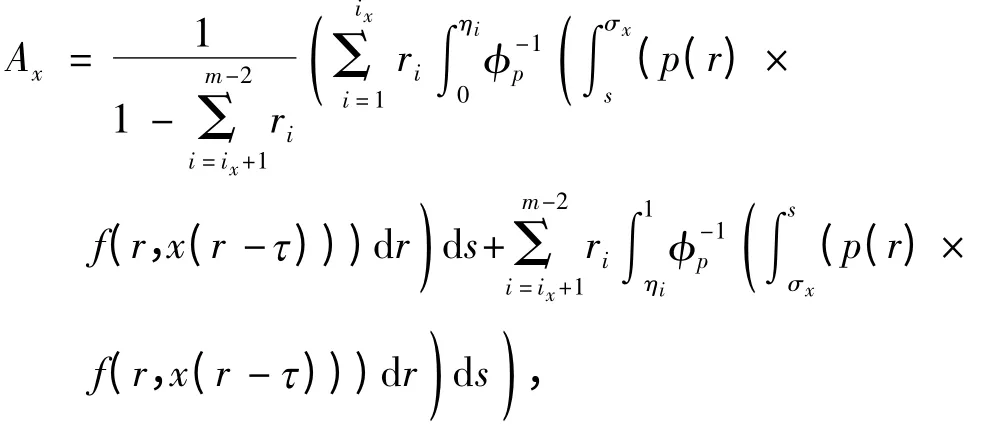
其中ix为不大于σx的最大的ηi的下标.显然，x 为边值问题(1)的解当且仅当x 为算子T 的不动点.

引理2 T 为P→P 的全连续算子. 进一步，若f(t，x)关于x 非减，则T 为增算子.

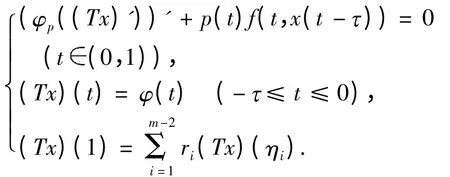
利用引理1 和Arzela－Ascoli 定理易知T 为P→P的全连续算子.

对任意的x1，x2P，若x1≤x2，则利用f 的单调性易知

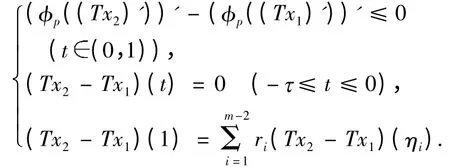
若Tx2＜Tx1，则存在t0［0，1］使得

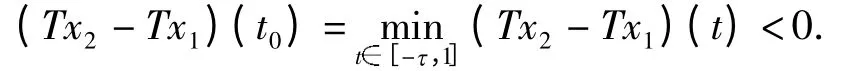
由于(Tx2－Tx1)(0)=0，故t0(0，1］.如果t0=1，则

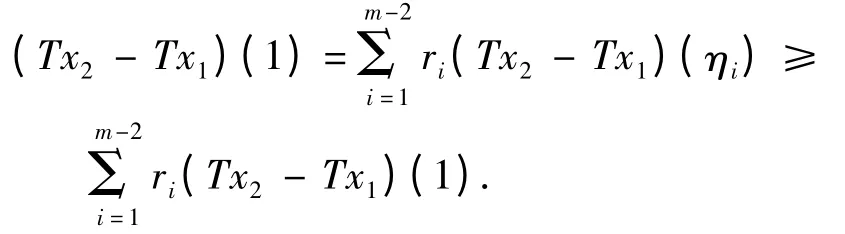
其中至少一个严格不等式成立.再结合φp的单调性可知

其中至少一个严格不等式成立.

另一方面，由(φp(Tx2)')'－ (φp(Tx1)')'≤0(t(0，1))可知(φp((Tx2)')－φp((Tx1)'))(t)在(t0－δ，t0+δ)内单调递减，再利用(Tx2－Tx1)'(t0)=0 和φp的单调性可知

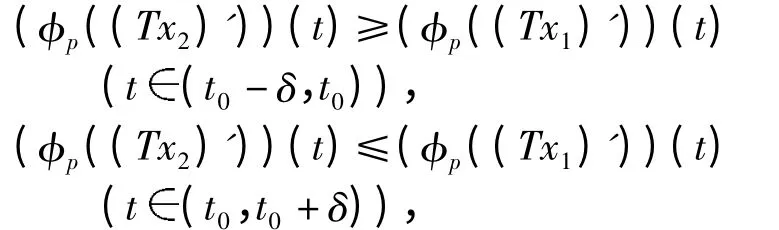
显然和前面的结论矛盾. 因此，Tx2≥Tx1成立，也即T 为增算子.

2 主要结果及证明

定理1 设条件(A1)～(A3)成立，若存在常数a≥M0，满足

(C1)f(t，x1)≤f(t，x2)，对任意的0≤t≤1，0≤x1≤x2≤a，

(C2)t

(C3)f(t，0)在(τ，1)内不恒等于零，则边值问题(1)存在正解α，β 满足

(1) α ≤a，β ≤a;

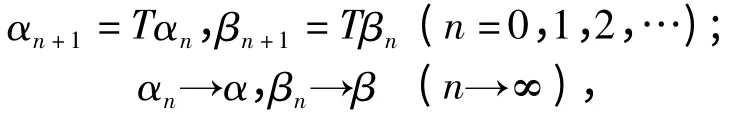
其中

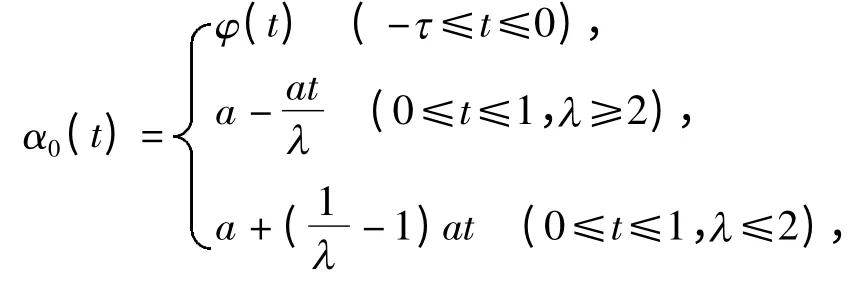
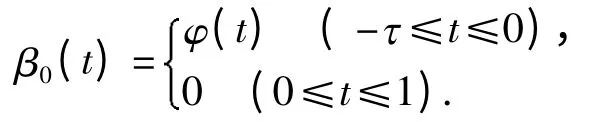
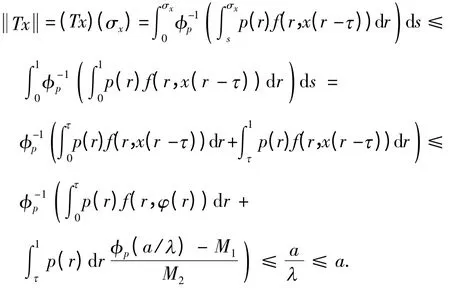
故TPa⊆Pa.

根据α0的定义易知α0Pa.令αn+1=Tαn(n=0，1，2，…)，则αnPa(n =0，1，2，…). 结合条件(C1)、(C2)可知

再利用T 的定义可得

即α1≤α0. 由引理2 可知T 为全连续的增算子，故αn+1≤αn(n=0，1，2，…)且序列一致收敛，若记，则αPa且Tα =α，因此α 为边值问题(1)的解.

显然有β0Pa.记βn+1=Tβn=Tn+1β0(n =0，1，2，…)，利用TPa⊆Pa易得βnPa，从而有β1≥β0，再结合T 的单调性可知Tβ1≥Tβ0，即β2≥β1，进一步可知βn+1≥βn(n=0，1，2，…).因为T 的紧性不难知道序列一致收敛. 令，则βPa且β 为T 的不动点，因此β 为边值问题(1)的解.

由条件(C3)易知β0不是边值问题(1)的解，再利用α(t)和β(t)的凹性可得

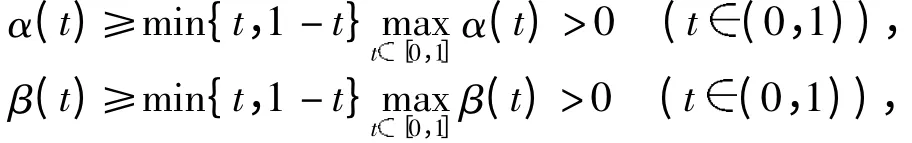
因此，α，β 均为边值问题(1)的正解.

例1 考虑边值问题

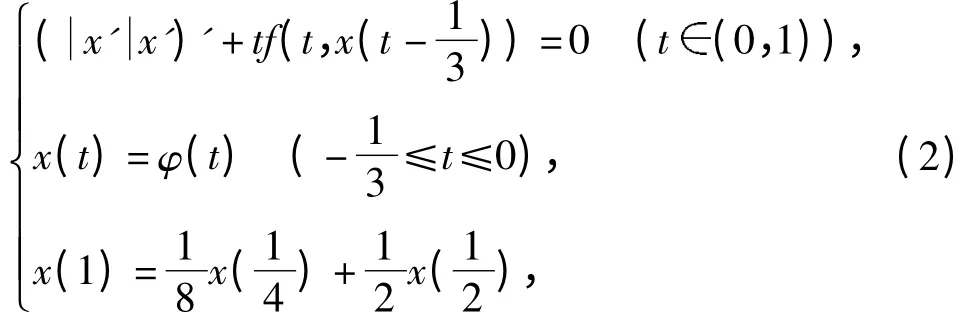
对照边值问题(1)可知p(t)=t，τ =1/3，η1=1/4，η2=1/2，r1=1/8，r2=1/2. 选取a =8，经过简单的计算可知λ =8/3，M0=1 ＜a，M1=1/24，M2=4/9，从而易得对任意的0≤t≤1，0≤x1≤x2≤5，

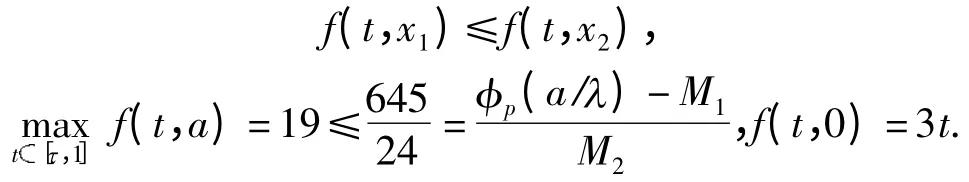
显然，定理1 的所有条件得到满足，进而可知边值问题(2)存在正解α，β 满足

(1) α ≤8，β ≤8;

其中

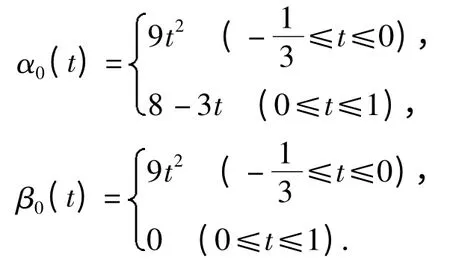
［1］许钊泉，翁佩萱. 一类具有反馈控制Logistic 模型周期解的存在性及全局吸引性［J］.华南师范大学学报:自然科学版，2010(3):19－23.

［2］宋利梅. 一类二阶非线性中立型微分方程周期解的存在性［J］.华南师范大学学报:自然科学版，2010(2):27－31.

［3］BAI Dingyong，XU Yuantong. Existence of positive solutions for boundary－value problems of second－order delay differential equations［J］. Appl Math Lett，2005，18(6):621－630.

［4］WANG Youyu，ZHAO Wenxia，GE Weigao. Multiple positive solutions for boundary value problems of second order delay differential equations with one－ dimensional p－Laplacian［J］.J Math Anal Appl，2007，326(1):641－654.

［5］SHU Xiaobao，XU Yuantong. Triple positive solutions for a class of boundary value problems of second－order functional differential equations［J］. Nonlinear Anal，2005，61(8):1401－1411.

［6］MA Dexiang，DU Zengji，GE Weigao.Existence and iteration of monotone positive solutions for multipoint boundary value problem with p－Laplacian operator［J］. Comput Math Appl，2005，50(5):729－739.

［7］SUN Bo，GE Weigao. Existence and iteration of positive solutions to a class of Sturm－Liouville－like p－Laplacian boundary value problems［J］.Nonlinear Anal－THEOR，2008，69(4):1454－1461.

［8］PANG Huihui，FENG Meiqiang，GE Weigao. Existence and monotone iteration of positive solutions for a three－point boundary value problem［J］.Appl Math Lett，2008，21(7):656－661.

［9］WANG Weibing，SHEN Jianhua. Positive solutions to a multi－point boundary value problem with delay［J］. Appl Math Comput，2007，188(1):96－102.

［10］DU Bo，HU Xueping，GE Weigao. Positive solutions to a type of multi－ point boundary value problem with delay and one－ dimensional p－ Laplacian［J］. Appl Math Comput，2009，208(2):501－510.