稳态扩散问题中Tikhonov正则化系数的收敛率

李 景，郭柏灵

(1. 长沙理工大学数学与计算科学学院，湖南长沙410004;2. 北京应用物理与计算数学研究所，北京100088)

近年来，数学物理反问题得到越来越多的关注［1-7］.其应用覆盖人体内部的重构、地质探测、遥感技术、图像处理和经济决策等方面. 本文主要探讨稳态扩散方程中系数的识别问题.

令Ω 是N中分片光滑的有界开区域，其边界Γ=∂Ω，其中Γ=Γc∪Γi且Γc∩Γi=∅.

考虑如下稳态扩散方程:

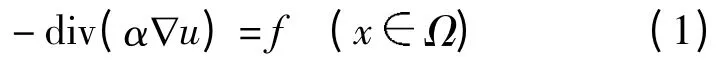
且带有边界条件

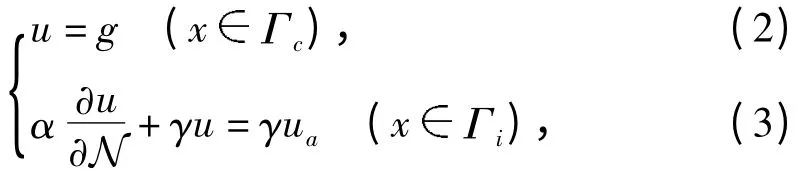
这里，α(x)表示热传导系数且满足

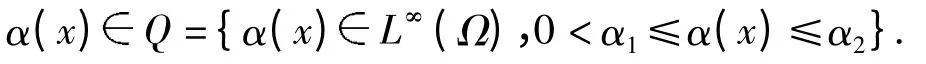
系统(1)～(3)可用来模拟稳态扩散过程以及传导体和周围环境的对流过程［8］和热传导过程［9-10］. 这个模型吸引了很多工程学家和数学家的兴趣.特别地，对工程家来说，传导系数α(x)和Robin 系数γ(x)有着非常重要的物理意义. 但是许多情形下，这2个系数是未知的，而且难于求解.因此，为了求解这些系数，出现了下面2个常见的反问题研究:

反问题1 能否利用u(x)的某些测量数据求出未知的Robin 系数γ(x)?

针对这个问题，已经有大量的数值方法［6，11-13］利用边界测量数据来重构Robin 系数γ(x). 结合Modica-Mortola 泛函，JIN 等［12］利用所讨论反问题的变分形式来求解γ(x). 而在文献［13］中，JIN 等首先构造极小化泛函，然后通过共轭梯度法求解此泛函的解(即为γ(x)的近似解)，理论分析得出L∞-收敛性. CHAABANE 等［11］利用Kohn-Vogelius价格函数，在某个允许集Φad重构了γ(x).

反问题2 假设u(x;α)(本文主要讨论u(x;α)与α 之间的联系，下文为方便起见，u(x;α)简记为u(α))是系统(1)～(3)的解. 若测量出的实际温度具有误差，这里用zδ表示实际测量温度，那么如何利用测量的温度去重构α(x)呢?

众所周知，这个问题在Hardmard 意义下是不适定的. 关于传导系数α(x)的重构问题也已经有了大量的研究结果. 例如，HÀO 等［4］讨论了∂Ω 边界上齐次Cauchy 问题的α(x)的识别问题，并得出了正则解的收敛率. CHAN 等［14］利用Lagrangian 变分方法求解α(x). KNOWLES［15］则利用共轭梯度算法计算非齐次Cauchy 问题中的α(x).

1 极小化泛函的稳定性

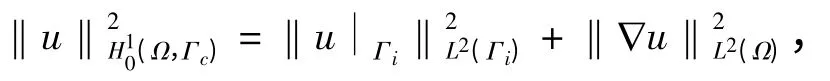
此范数等价于‖·‖H1(Ω).

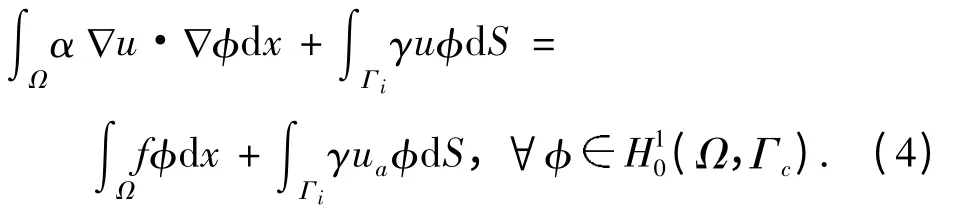
贯穿全文，用c 表示任何一个可依赖于αi，γi(i=1，2)或 文 中 其 他 已 知 量(如‖ f ‖(H1(Ω))'，‖g‖H1/2(Γc)，‖ua‖H-1/2(Γi))的常数. 为证明收敛率，首先给出如下定理.

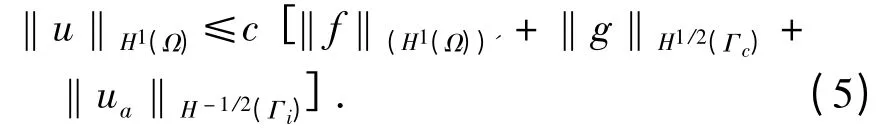
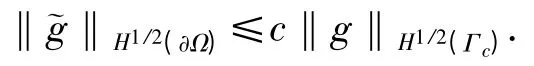
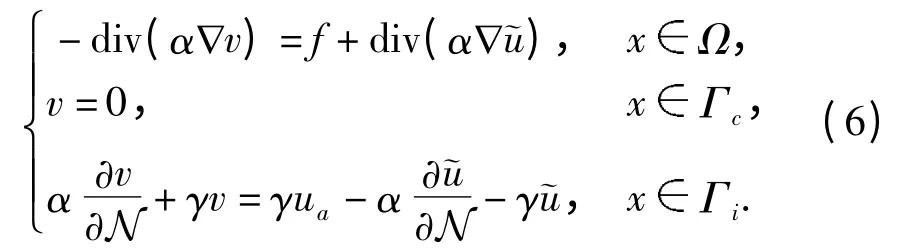
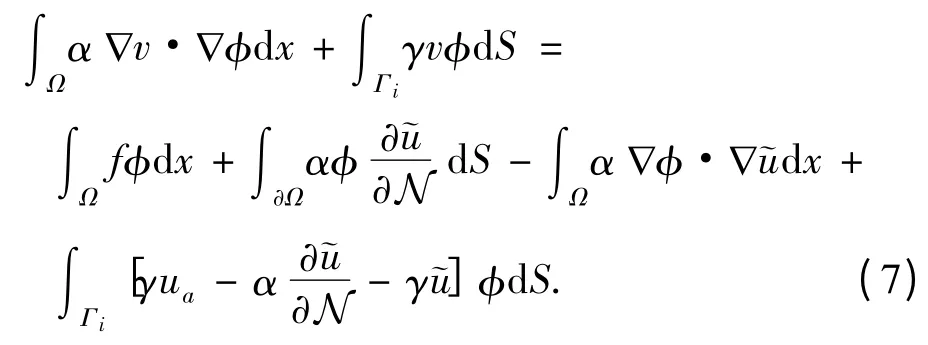
上式中取φ=v，有

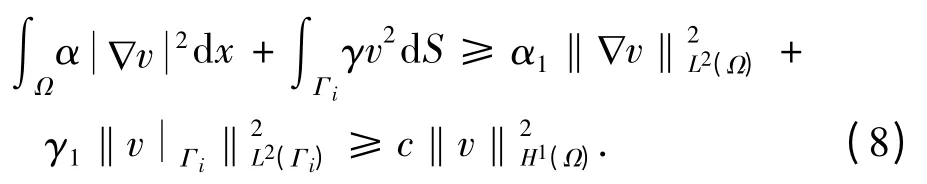
由迹定理知

因而，结合式(7)和式(9)，得

通过精益管理系统授权员工，鼓励员工参与日常工作改善活动，并培养员工持续改进能力；建立战略展开系统，确立恩泽真北目标，形成共识机制，建立持续改进文化，最终助力恩泽医疗成功转型，提高医院运营绩效，为患者和员工创造价值。

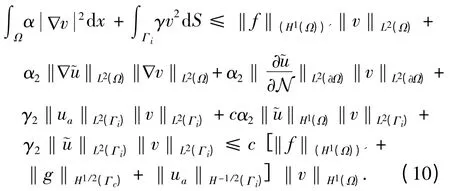
联立式(8)和式(10)，得

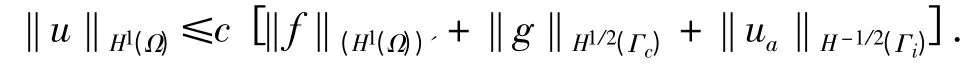
证毕.

引理1 令u(α)是问题(1)～(3)的解，那么映射u:Q ⊂L∞(Ω)→H1(Ω)在集合Q 上连续Fréchet 可微. 此外，对于每个αQ，u(α)的Fréchet导数u'(α)满足η=u'(α)h，hL∞(Ω)是下述问题在(Ω，Γc)中的弱解:

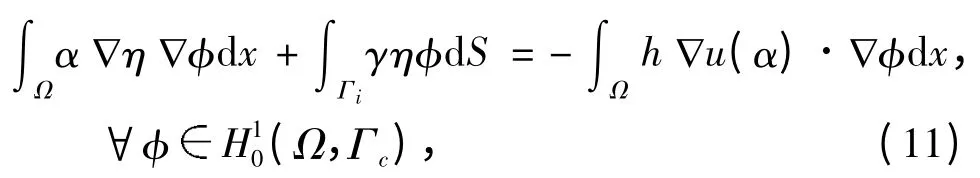
而且

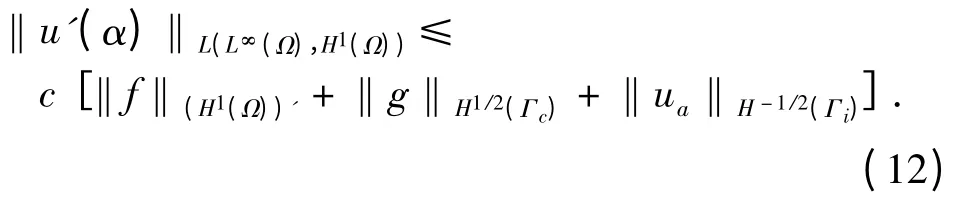
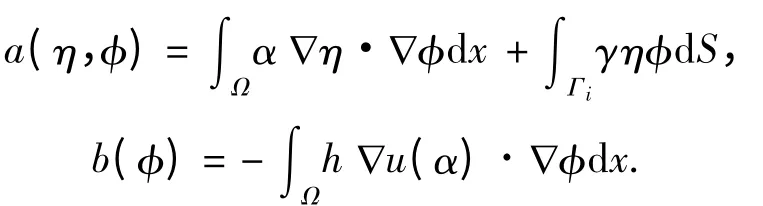
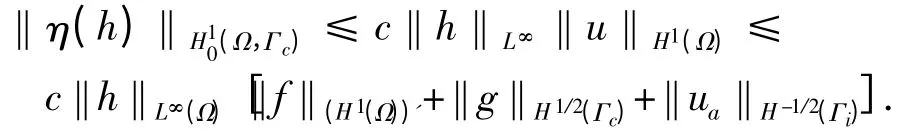
由式(4)可得

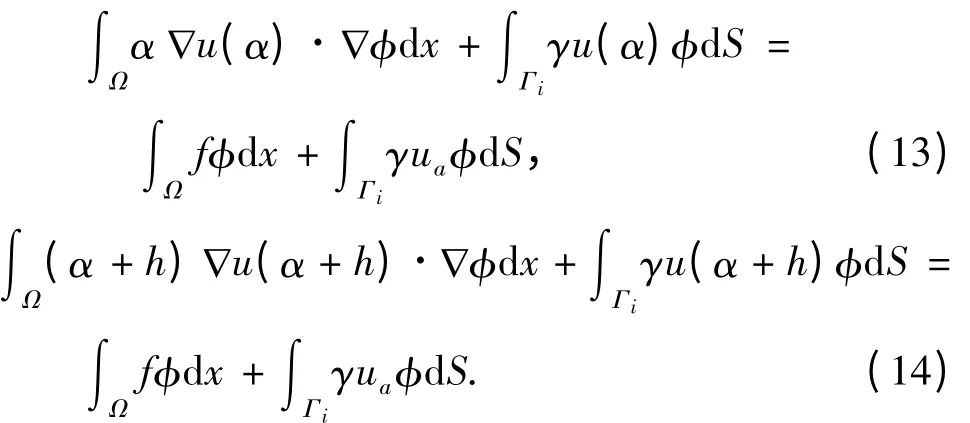
式(13)与式(14)相减，得

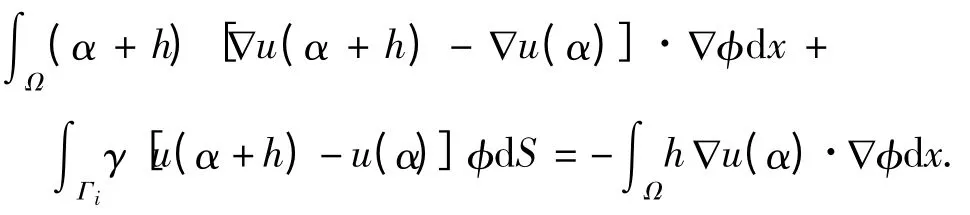
于是

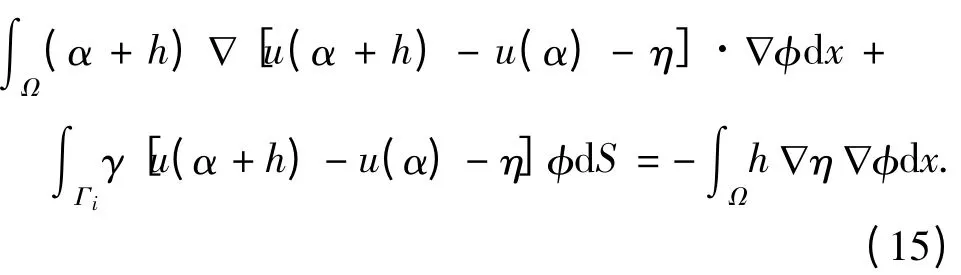
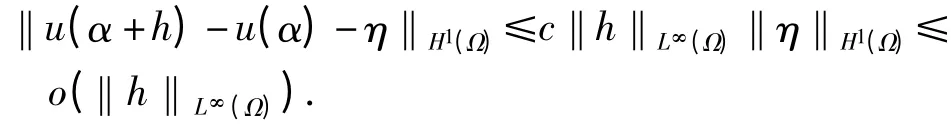
因η 关于h 是从L∞(Ω)到(Ω，Γc)的有界线性算子，从而u(α)连续Fréchet 可微，且其导数u'(α)h 即为η.

注1 u'(α)的对偶算子可表示如下

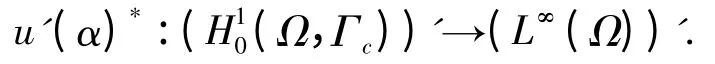
接下来将构造合适的Tikhonov 极小化泛函，利用此泛函的极小解去逼近所求传导系数，并证明其收敛率.定义

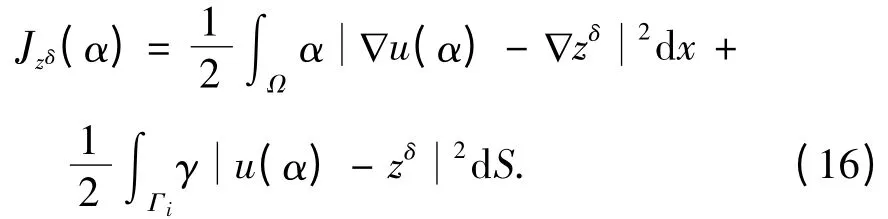
上述泛函具有如下性质:

引理2 Jzδ(α)在Q 上是凸的而且下半连续.

证明 Jzδ(x)在Q 上是连续的. 下面仅需证明Jzδ(α)的凸性. 通过简单计算，对任意的hL∞(Ω)有

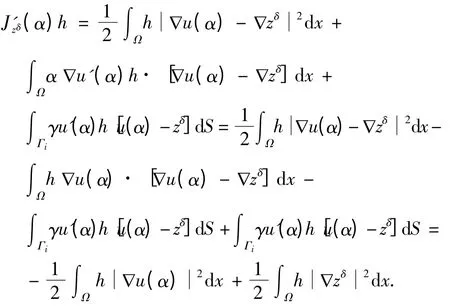
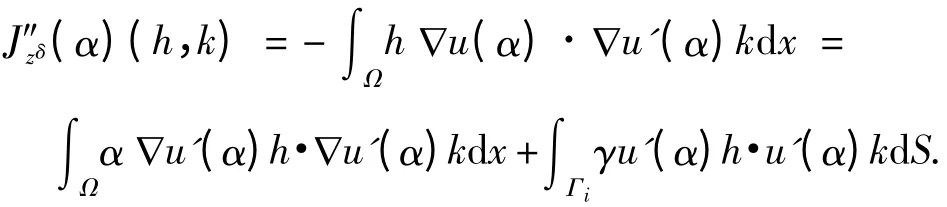
因而，

于是Jzδ(x)在Q 上是凸的. Jzδ(α)的下半连续性可由Jzδ(α)的凸性和连续性得出.

定义

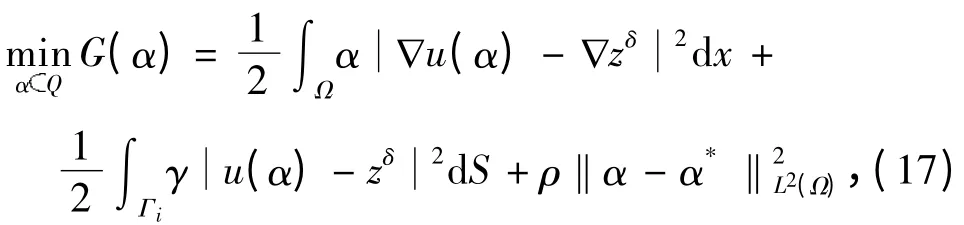
这里，ρ 表示正则化参数，α*是精确传导系数α+的先验估计值.

从上述引理可以看出，G(α)在Q 上下半连续且严格凸，从而存在唯一的极小值，我们用αδρ 来表示.

下面给出G(α)的稳定性.

定理2 设在H1(Ω)中，zn→zδ且{αn}是式(17)中zδ替换为zn后G(α)的极小解. 那么αn→

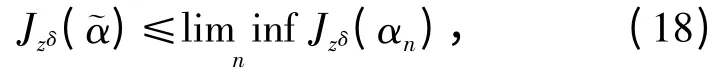
且

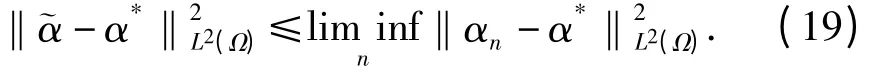
又因

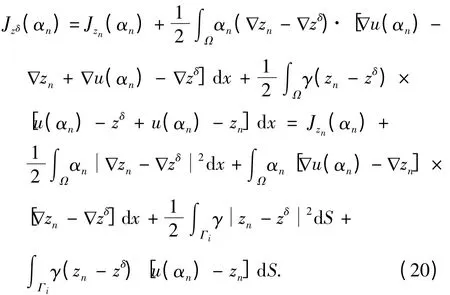
故由u(αn)在H1(Ω)中的有界性及式(20)，得

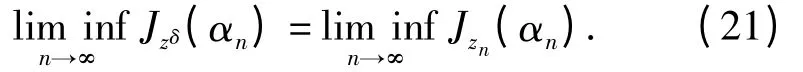
联立式(18)、(19)和式(21)得

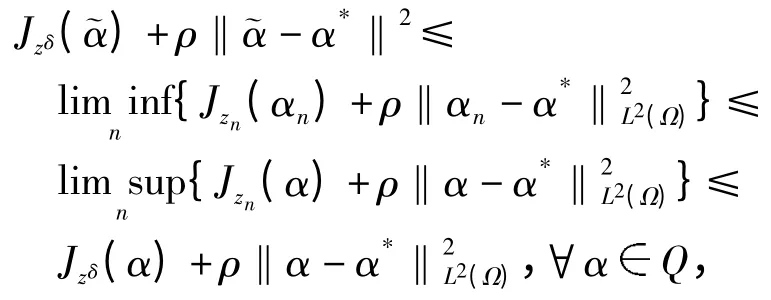
2 近似传导系数的收敛率

首先，假定α+是精确的传导系数，u+=u(α+)是边值问题(1)、(3)的解.zδ为Ω 上u(x)的测量数据，且满足

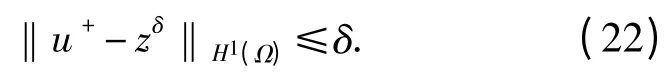
注2 由式(4)知，传导系数α(x)可由测量数据uδ唯一确定［7］.

接下来给出收敛率的结果.

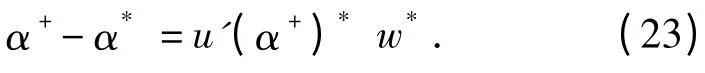
那么如果ρ=O(δ)，则

证明

由式(22)及迹定理可知

另一方面，

考虑如下问题:

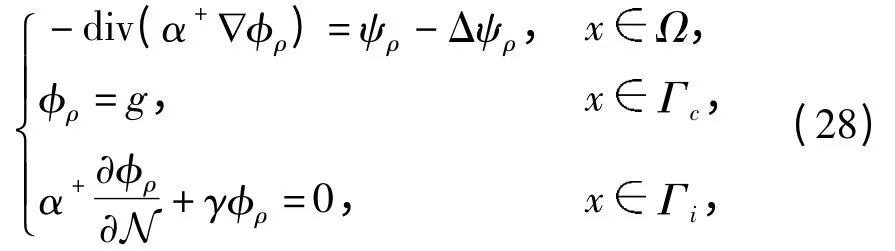
这里ψρ(Ω)(0 ＜ρ ＜1)在H1(Ω)中一致有界，且满足

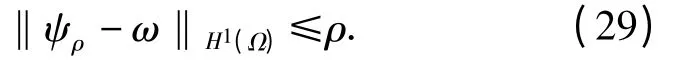
那么由格林公式得利用分部积分和Cauchy -Schwarz 不等式，可以得出，存在常数C ＞0，使得

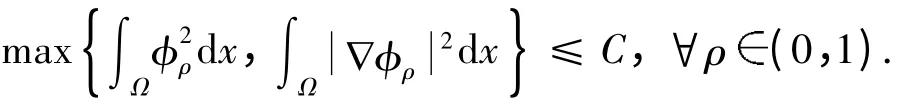
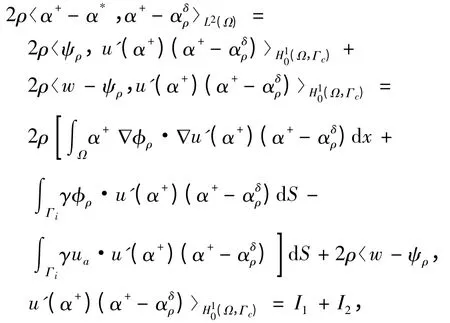
这里，

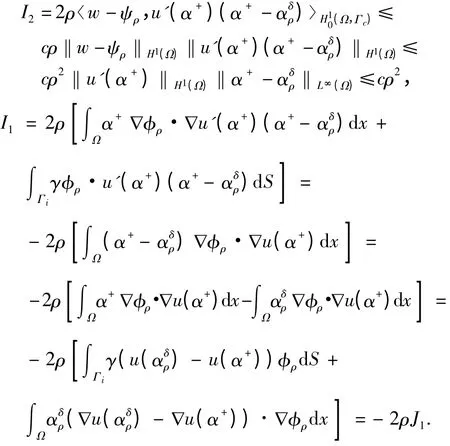
现在估计J1. 再次利用迹定理及Cauchy - Schwarz不等式可得

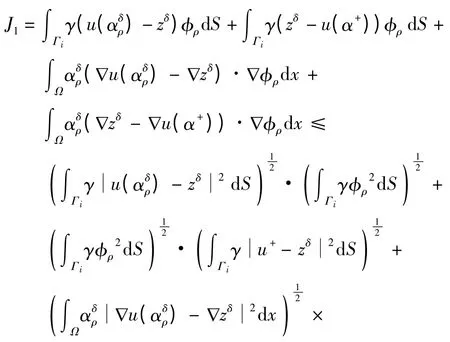
结合上述所有不等式，可得

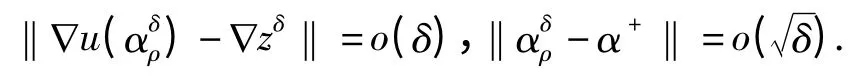
因而，定理得证.

［1］CHENG J，PENG L，YAMAMOTO M. The conditional stability in line unique continuation for a wave equation and an inverse wave source problem［J］. Inverse Probl，2005，21:1993 -2007.

［2］金华. 可交换条件下具有测量误差的结构回归模型［J］.华南师范大学学报:自然科学版，2007(2):1-6.

［3］ENGL H W，HANKE M，NEUBAUER A. Regularization of inverse problems［M］. Dordrecht:Kluwer，1996.

［4］HÀO D N，QUYEN T N. Convergence rates for Tikhonov regularization of coefficient identification problems in Laplace- type equation［J］. Inverse Probl，2010，26:125014.

［5］HÀO D N，DUC N V. Stability results for backward parabolic equations with time - dependent coefficients［J］.Inverse Probl，2011，27:025003.

［6］INGLESE G. An inverse problem in corrosion detection［J］. Inverse Probl，1997，13:977 -994.

［7］ISKOV V. Inverse problem for partial differential equation［M］. 2nd ed. New York:Springer，2006.

［8］OSMAN A M，BECK J V. Nonlinear inverse problem for the estimation of time-and-space dependent heat transfer coefficients［J］. J Thermophys Heat Transf，1999，3:146 -152.

［9］WHITE F M. Heat and mass transfer［M］. New York:Addison-Wesley，1988.

［10］KAUP P G，SANTOSA F. Nondestructive evaluation of corrosion damage using electrostatic measurements［J］. J Nondestr Eval，1995，14:127 -136.

［11］CHAABANE S，ELHECHMI C，JAOUA M. A stable recovery method for the Robin inverse problem［J］. Math Comput Simul，2004，66:367 -383.

［12］JIN B T，ZOU J. Numerical estimation of piecewise constant Robin coefficient［J］. SIAM J Control Optim，2009，48:1977 -2002.

［13］JIN B T，ZOU J. Numerical estimation of the Robin coefficient in a stationary diffusion equation［J］. IMA J Numer Anal，2010，30:677 -701.

［14］CHAN T F，TAI X C. Identification of discontinuous coefficients in elliptic problems using total variational regularization［J］. SIAM J SCI Comput，2003，25:881 -904.

［15］KNOWLES I. Parameter identication for elliptic problems［J］. J Comput Appl Math，2001，131:175 -194.

［16］STEINBACH O. Numerical approximation method for elliptic boundary value problems:Finite and boundary elements［M］. Austria:Springer，2008.