有序Banach空间非线性四阶边值问题的正解

张旭萍，李永祥

(西北师范大学数学与信息科学学院，甘肃兰州730070)

设E 为有序Banach 空间，其正元锥P 为正规锥，正规常数为N，记Ⅰ=［0，1］，考虑E 中的非线性四阶边值问题

正解的存在性，其中f:［0，1］×E×E→E 连续，θ 为E 中的零元.

Banach 空间中的常微分方程作为含无穷维参数的常微分方程及无穷维常微分方程组的抽象模型，是微分方程中的一个重要研究课题. 由于无限维空间与有限维空间的本质差异，普通常微分方程的许多研究结果，特别是解的存在性结果对抽象空间的常微分方程不再成立，因此研究抽象空间常微分方程解的存在性理论与应用都是有意义的. 当E= 时，问题(1)已被一些学者做过大量的研究［1－4］. 但在一般的抽象空间中，对该问题的研究相对较少. 文献［1］利用锥上全连续算子的不动点指数理论解决了当E= 时，边值问题(1)正解的存在性问题，但在抽象空间中，至今未出现任何相关结论. 本文主要利用凝聚映射拓扑度理论及相关的不动点定理，在Banach 空间中研究四阶两点边值问题(1)正解的存在性问题，并给出了存在性定理，从而推广了文献［1］的结果.文献［5］－［6］在非紧性测度条件下讨论Banach 空间常微分方程边值问题时，要求非线性项f 在有界集上一致连续.本文采用了新的非紧性测度的估计技巧，删去了对f 一致连续的要求.

1 预备工作

问题(1)可化为Banach 空间中等价的积分方程

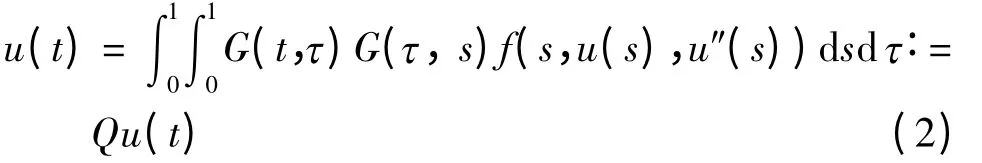
来处理，其中

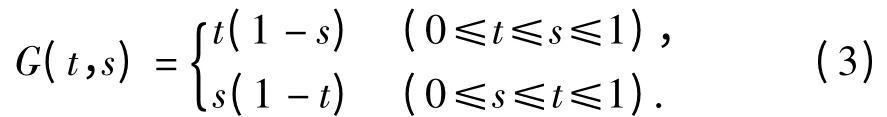
设E 为Banach 空间，用· 表示E 中的范数.C(Ⅰ，E)为定义于Ⅰ取值于E 的全体连续函数按范数构成的Banach 空间. 在C2(Ⅰ，E)中取等价范数‖u‖2= max{‖u‖c，‖u″‖c}，则C2(Ⅰ，E)按‖u‖2构成了Banach 空间. 记K2(Ⅰ，P)={uC2(Ⅰ，E)|u≥θ，u″≤θ}，则K2(Ⅰ，P)为C2(Ⅰ，E)中的正规锥，正规常数亦为N.

先引入一些非紧性测度的有关结果. 以下E 与C(Ⅰ，E)中有界的Kuratowski 非紧性测度均用α(·)表示，C2(Ⅰ，E)中有界的Kuratowski 非紧性测度用α2(·)表示. 对B⊂C(Ⅰ，E)，记B(t)={u(t)|uB，tⅠ}⊂E. 对B⊂C2(Ⅰ，E)，记B″(t)={u″(t)|uB，tⅠ}.

假设f 满足非紧性测度条件(H0):∀R ＞0，f 在Ⅰ×PR×(－PR)上有界，且存在常数L1和L2，满足L1+L2＜2，使得对∀tⅠ，D1⊂PR，D2⊂(－PR)，有

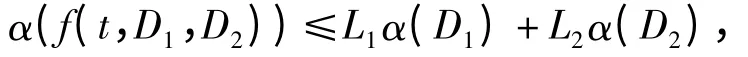
设Q 为由方程(2)定义的算子，则Q:K2(Ⅰ，P)→K2(Ⅰ，P)连续，且易验证方程(1)的解等价于Q 的不动点.本文将应用凝聚映射的不动点指数理论寻找Q 的不动点. 本节先证明在条件(H0)下，Q:K2(Ⅰ，P)→K2(Ⅰ，P)是凝聚的.

引理1［6］设B⊂C(Ⅰ，E)为等度连续的有界函数簇，则α(B)在Ⅰ上连续，且

引理2［7］设B ={un}⊂C(Ⅰ，E)为可列集，若存在ψL1(Ⅰ)，使得‖un(t)‖≤ψ(t)，a.e tⅠ，n=1，2，…，则

引理3［8］设D⊂E 有界，则存在D 的可列子集D0，使得α(D)≤2α(D0).

引理4 假设条件(H0)成立，则方程(2)定义的算子Q:K2(Ⅰ，P)→K2(Ⅰ，P)凝聚.

证明 易见Q 把K2(Ⅰ，P)中的有界集映为有界的等度连续集. 任取非相对紧的有界集B⊂K2(Ⅰ，P)，则Q(B)和Q(B″)是有界的等度连续集，由非紧性测度的定义及性质可得

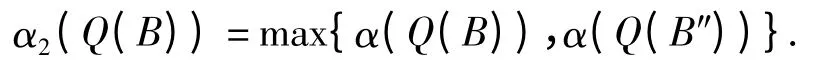
由引理3 知，存在可列集B0= {un}⊂B，使得α(Q(B))≤2α(Q(B0))，α(Q(B″))≤2α(Q(B″0)).对∀tⅠ，由引理2 及假设(H0)，有

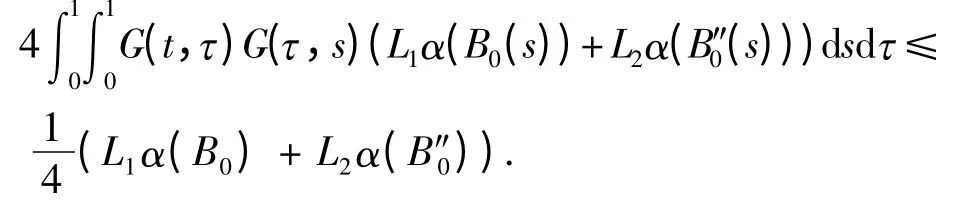
所以

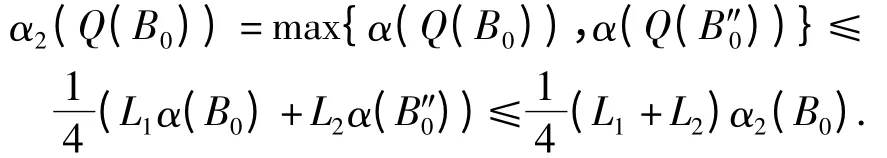
因此

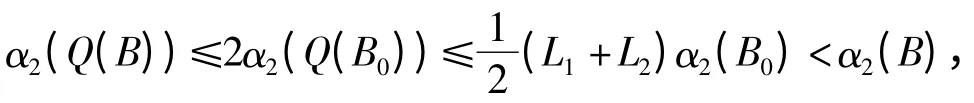
从而Q:K2(Ⅰ，P)→K2(Ⅰ，P)为凝聚映射. 证毕.

由式(3)易知:Green 函数G(t，s)具有性质:

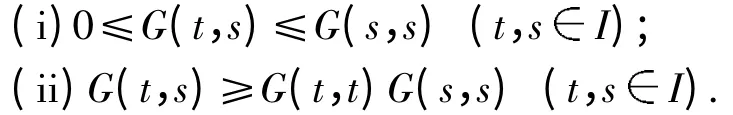
取K2(Ⅰ，P)的子锥

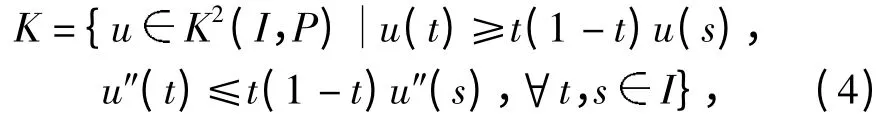
由性质(i)与(ii)易证，Q(K2(Ⅰ，P))⊂K，因此Q:K→K 为凝聚映射，问题(1)的正解等价于Q 在K 中的非零不动点.对0 ＜r ＜R ＜∞，记

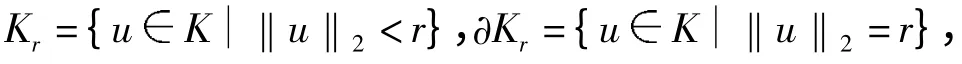
∂Kr为Kr在K 中的相对边界，记，则Q在Kr，R上的不动点为问题(1)的正解.本文将在Kr，R上应用凝聚映射的不动点指数理论寻求Q 的不动点.

设X 为Banach 空间，K⊂X 为闭凸锥，Ω⊂X 为有界开集为凝聚映射，若Q 在K∩∂Ω 上无不动点，则不动点指数i(Q，K∩Ω，K)有定义.i(Q，K∩Ω，K)有与全连续映射的不动点指数完全类似的性质，所不同的是同伦不变性条件需由紧同伦改为一致凝聚同伦. 一个重要的性质是可解性:若i(Q，K∩Ω，K)≠0，则Q 在K∩Ω 中存在不动点，利用同伦不变性与可解性，能够用与全连续映射情形相同的论证方法证明i(Q，K∩Ω，K)具有下列性质:

引理5(零伦性) 设Q:K→K 为凝聚映射，r ＞0，若Q 满足u≠λQu，∀u∂Kr，0 ＜λ≤1. 则不动点指数i(Q，Kr，K)=1.

引理6(缺方向性) 设Q:K→K 为凝聚映射，r ＞0，若存在v0K，v0≠θ，使得u－Qu≠τv0，∀u∂Kr，τ≥0.则不动点指数i(Q，Kr，K)=0.

2 主要结果

定理1 设E 为有序Banach 空间，其正元锥P为正规锥. 设f:Ⅰ×P×(－P)→P 连续，且满足假设(H0)，若f 满足条件:

(H1)∃α，β≥0，α/π4+β/π2＜1，及r0＞0，使得f(t，u，v)≤αu－βv，∀tⅠ，uPr0，v(－Pr0);

(H2)∃α1，β1≥0，α1/π4+ β1/π2＞1，及h1C(Ⅰ，P)，使得

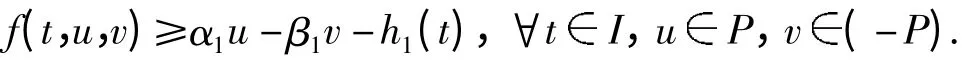
则边值问题(1)至少存在一个正解.

证明 按上一节讨论，只需证明由方程(2)定义的凝聚映射Q:K→K 存在非平凡的不动点. 取0 ＜r ＜R ＜∞，证明当r 充分小、R 充分大时Q 在Kr，R中 存 在 不 动点. 取r(0，r0)，其中r0为 条 件(H1)中的常数，证明Q 满足引理5 的条件:

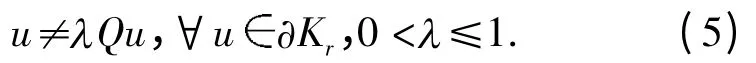
反设式(5)不成立，则存在u0∂Kr，及0 ＜r0≤1，使得u0=λ0Qu0，按Q 的定义，u0满足微分方程

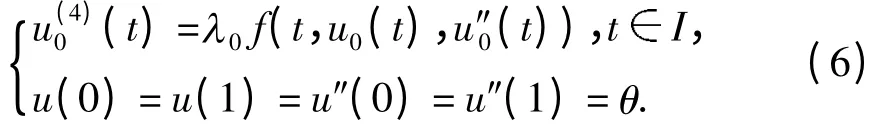
因为u0(t)，u″0(t)Kr0，由条件(H1)有(t)≤f(t，u0(t)，u″0(t))≤αu0(t)－βu″0(t)，tⅠ. 上式两边同乘以sin(πt)，然后在Ⅰ上积分有

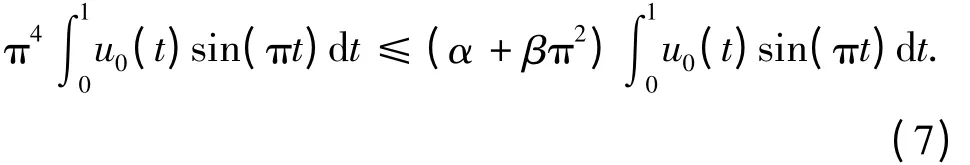
由条件(H1)知π4＞α+βπ2，则θ. 另一方面，因为u0K，按锥K 的定义，

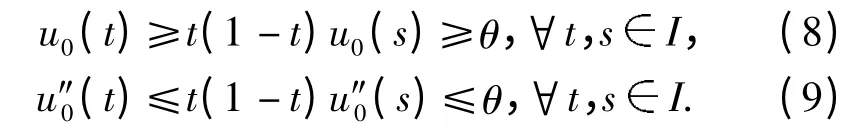
对式(8)两边同乘以sin(πt)，然后在Ⅰ上积分可得

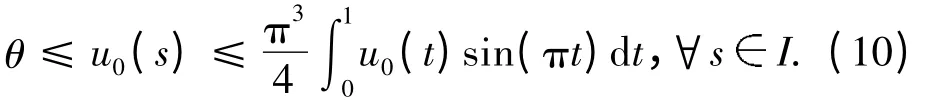
令v0=－u″0，则v0(t)≥t(1－t)v0(s)，易得

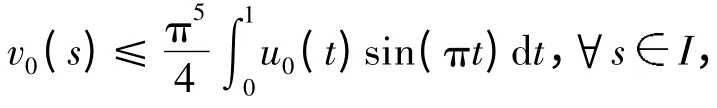
则

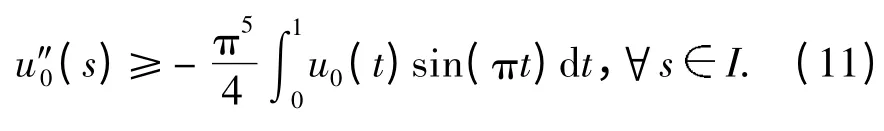
从而

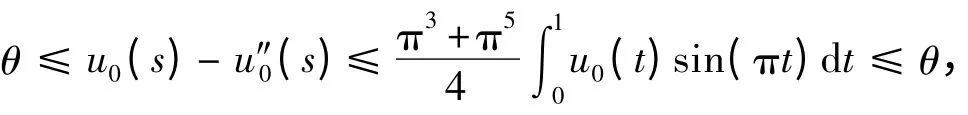
因此u0(s)－u″0(s)≡θ 于Ⅰ.但u0(s)≥θ，－u″0(s)≥θ，故u0(s)=－u″0(s)≡θ. 从而‖u0‖2=0. 这与u0∂Kr矛盾. 于是式(5)成立，故按引理5 有

取R ＞r0，eP，‖e‖=1，令v0(t)=esin(πt)，则v0K.以下证明当R 充分大时有

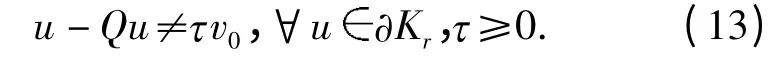
假设存在u0KR及τ0≥0，使得u0－Qu0=τ0v0，则Qu0=u0－τ0v0. 按Q 的定义，u0满足微分方程

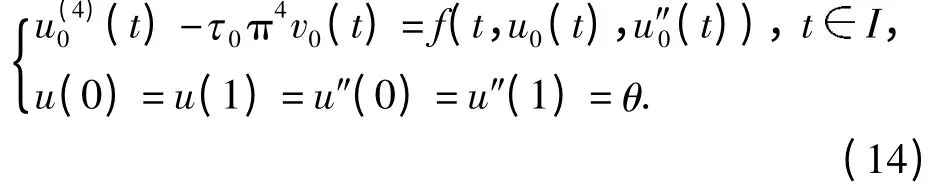
因此，按假设(H2)有

上式两边同乘以sin(πt)，然后在Ⅰ上积分得

因此

结合式(9)与式(10)有

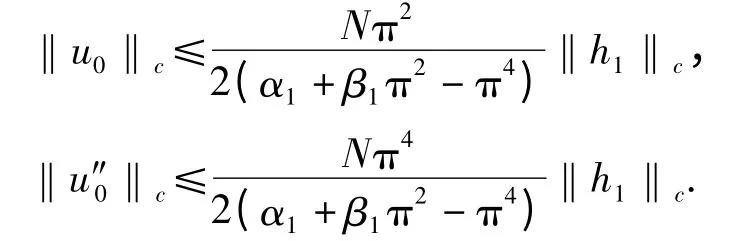
从而

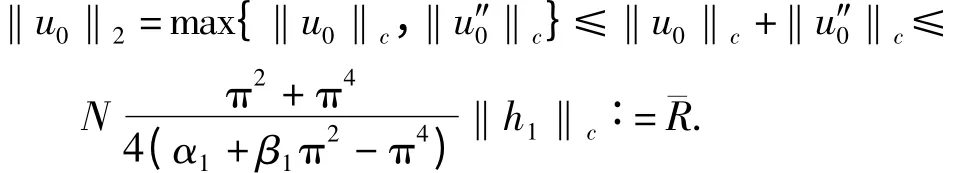
于是按不动点指数的区域可加性及式(11)、(14)有

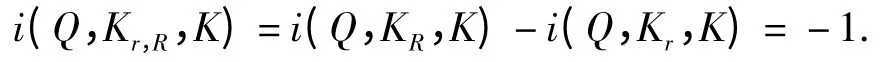
因此按可解性，Q 在Kr，R中存在不动点，该不动点为问题(1)的正解. 证毕.

定理2 设E 为Banach 空间，其正元锥P 为正规锥. 设f:Ⅰ× P × (－ P)→P 连续，且满足假设(H0)，若f 满足条件

(H3)∃α，β≥0，α/π4+β/π2＞1，r1＞0，使得

(H4)P)，使得

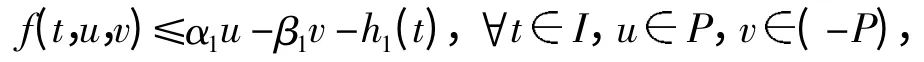
则边值问题(1)至少存在一个正解.

3 应用

考虑如下非线性四阶两点边值问题

其中Ⅰ=［0，T］，T 是一个常数.

结论:四阶两点边值问题(21)至少有一个解.

在C2(Ⅰ，E)中取等价范数‖u″‖c}，则C2(Ⅰ，E)按‖u‖2构成了Banach 空间.记K2则K2(Ⅰ，P)为C2(Ⅰ，E)中的正规锥.取K2(Ⅰ，P)的子锥易验证定理1 中的条件(H0)、(H1)和(H2)能被满足.证毕.

［1］LI Yongxiang. On the existence of positive solutions for the bending elastic beam equations［J］. Appl Math Comput，2007，189:821－827.

［2］翁佩萱. 四阶泛函微分方程边值问题的上下解方法［J］. 华南师范大学学报:自然科学版，2000(3):1－6.

［3］杨雯抒. 一类滞后型泛函微分方程边值问题的正解［J］. 华南师范大学学报:自然科学版，2004(1):32－37.

［4］LI Yongxiang. Two－ parameters nonresonance condition of forth－order boundary value problems［J］. J Math Anal Appl，2005，308:121－128.

［5］GUO Dajun，LAKSHMIKANTHAM V. Multiple solutions of two－point boundary value problems of ordinary differential equations in Banach spaces［J］. J Math Anal Appl，1988，129:211－222.

［6］郭大钧，孙经先. 抽象空间常微分方程［M］. 济南:山东科学技术出版社，1989:188－222.

［7］HEINZ H P. On the behavior of measure of noncompactness with respect to differential and integration of vectorvalue functions［J］. Nonlinear Anal，1983，7:1351－1371.

［8］李永祥. 抽象半线性发展方程初值问题解的存在性［J］.数学学报，2005，48(6):1089－1094.