具有阶段结构的多时滞SIR扩散模型的稳定性

吴 敏，翁佩萱

(华南师范大学数学科学学院，广东广州510631)

全世界每年都有成千上万的人们遭受着传染病所带来的痛苦，故传染病模型的研究得到广泛的关注［1］. 生态模型的建立和对其稳定性的研究［2］有助于控制传染病的传播. 1927年，KERMACK 和MCKENDRICK［3］建立了第一个传染病模型(简称KM 模型)，此后许多学者陆续引进SIS、SIR、SIRS等模型来描述不同种类型的传染病［4－6］，其中SIR传染病模型是一类重要的人口模型，并得到广泛的关注［7］. 另一方面，个体由于年龄阶段不同，会产生相应的一些与年龄阶段相关的疾病，因此关于具有阶段结构的模型研究的相关文献也有很多［8］.

2002年，XIAO 等［9］提出了一个阶段结构的SIR 模型并研究其动力行为. 他们将种群划分为成年和未成年两个阶段，并假设成年人口不染病，疾病只在未成年人口间传播，实际上，例如麻疹、腮腺炎、水痘和猩红热等疾病就只在未成年人中传播.他们研究的具体模型如下:

其中S(t)、Ⅰ(t)和R(t)分别表示未成年的易感类、染病类和具有免疫力的恢复类的人口密度，y(t)表示成年的人口密度. 假设方程中所有系数均为正常数，α 表示未成年人口的出生率，β (0 ＜β ＜1)表示新出生个体中具有终生免疫力的概率，(1－β)表示新出生个体中易感类的概率，b1表示易感类转变成染病类的转化率，b2表示染病类转变成恢复类的转化率，τ表示未成年个体的成熟期，r1、r2和r3分别表示易感类、染病类和恢复类的死亡率，由生物意义知r2≥r1. 最后，假设成年人口的死亡与成年人口数的平方成正比，比例常数记为r4.

江志超等［10］改进了文献［9］中的模型，考虑发生率为一般函数f(S(t))且疾病有潜伏期的阶段结构的SIR 模型:

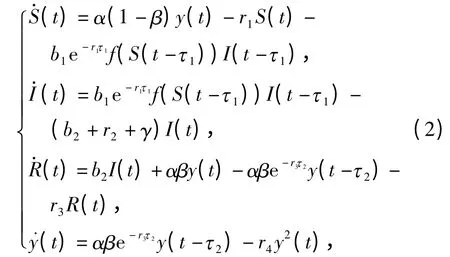
这里发生率f(S)满足f(0)=0 及f'(S)＞0，γ 表示因病死亡率，τ1表示疾病的潜伏期，τ2表示未成年个体的成熟期，其他系数具体意义与系统(1)一致.

一般来说，较常以常微分方程作为传染病模型，但它的局限在于仅有时间变量t. 而现实生活中，在一个国家甚至整个世界范围内的人口具有扩散性，故空间一致的模型与疾病和人口扩散的现实背景不相符. 近年来，为了解空间分布交互作用的最基本特征，学者在传染病模型的建立和模拟中，在相应的方程组中考虑了空间扩散的因素［11］.

本文考虑如下具有年龄阶段结构和时滞的空间扩散模型:

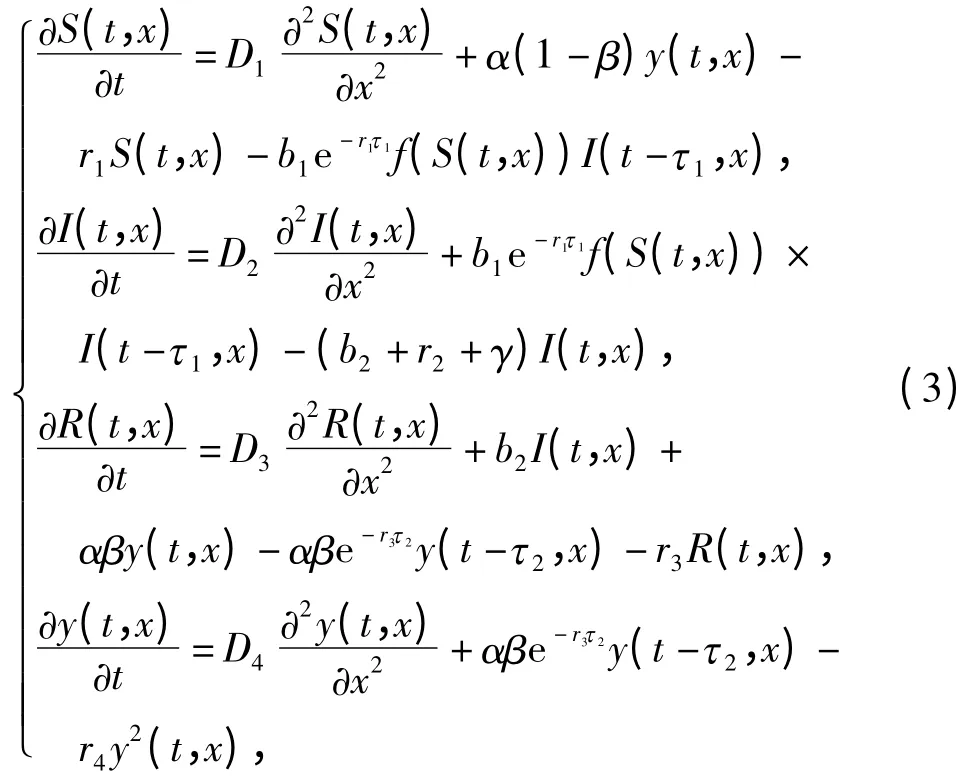
注意到系统(3)中的第3个方程可以由另外3个方程决定，因此我们仅需研究下面的子系统:

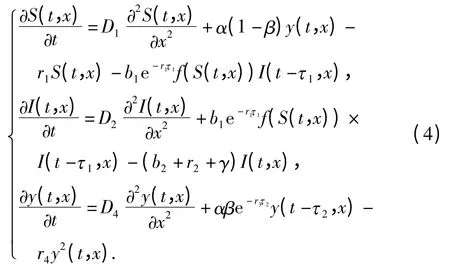
相应于子系统(4)，我们考虑下面的初值条件

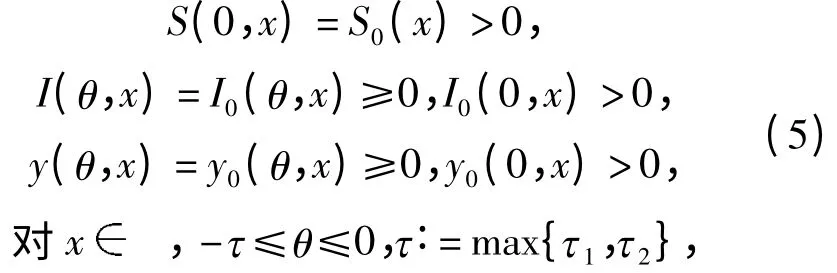
其中S0，Ⅰ0，y0都是其定义域中的连续函数.由于本文的主要目的是研究平衡态的稳定性，将不讨论初值问题解的存在性. 因此本文假设初值问题(4)和(5)的解全局存在并且保持非负.

经典传染病模型的重要特性之一是存在基本再生数R0.R0在疾病的传播中起着阈值的作用，并对疾病的控制有重要意义. 下面，我们给出R0的估计并讨论其在系统(4)的动力学行为中的阈值性质.通过计算，可以得到

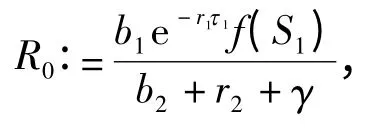
其中

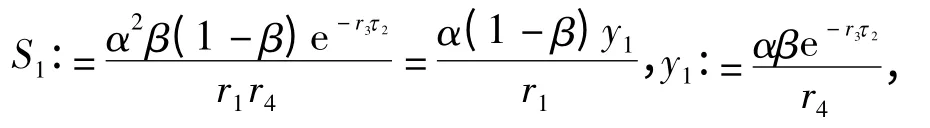
则在0 ＜R0＜1 和R0＞1 两种情形下可分别获得系统(4)的相应平衡点:

(i)若0 ＜R0＜1，系统(4)有2个平衡点:E0(0，0，0)和E1(S1，0，y1);

(ii)若R0＞1 且(其中Im f 是f在 +上的像集)，系统(4)有3个平衡点:E0(0，0，0)，E1(S1，0，y1)和E+(S+，Ⅰ+，y+)，其中y+=y1，且

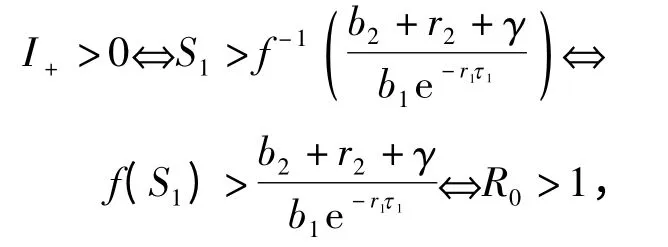
故R0＞1 是系统(4)的正平衡点存在的充要条件.

下面讨论平衡点的稳定性. 首先，将系统(4)在任一常数平衡点(S*，Ⅰ*，y*)处线性化得

线性方程组(6)具有形如:

的解当且仅当

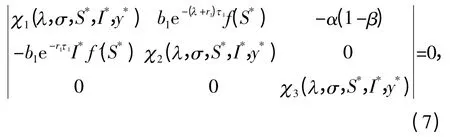
其中

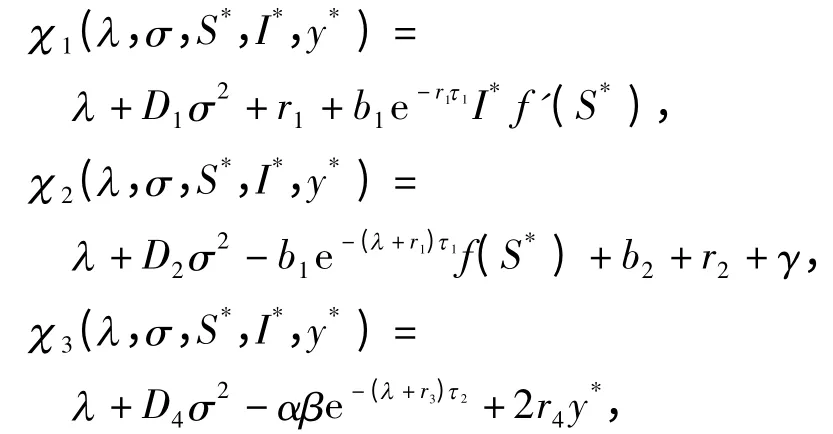
这里λ、σ 和i 分别为复数、实数和虚数单位. 式(7)等价于

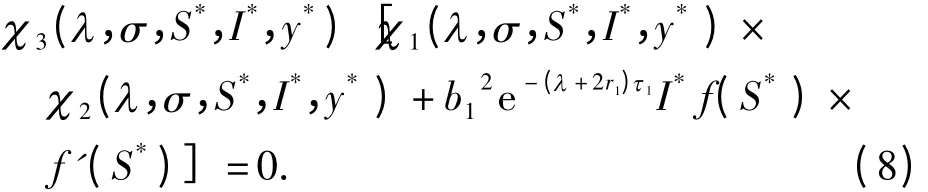
定理1 E0(0，0，0)是线性不稳定的.

证明 在式(8)中令(S*，Ⅰ*，y*)=(0，0，0)，则

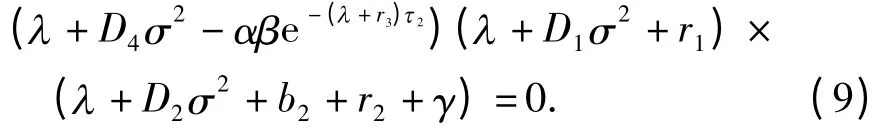
现断言至少有一对正数(λ*，σ*)满足式(9). 设

由g(0，σ)= D4σ2－ αβe－r3τ2知存在一个充分小的σ*＞0 使得

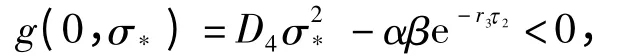
又g(λ，σ*)→∞当λ→∞，故方程g(λ，σ*)=0 有一个正根λ*. 因此，E0(0，0，0)是线性不稳定的.□

定理2 对平衡点E1(S1，0，y1)，有下面结论:

(i)若0 ＜R0＜1，则E1是线性渐近稳定的;

(ii)若R0＞1，则E1是线性不稳定的.

证明 在式(8)中令(S*，Ⅰ*，y*)=(S1，0，y1)，则有

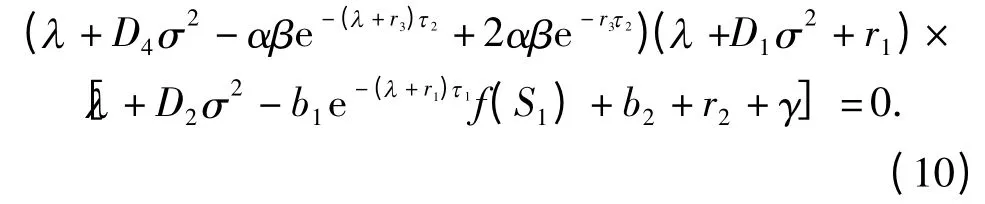
显然方程λ +D1σ2+r1=0 的根为负数.

令式(10)的第1个因式等于零得

下面证明方程(11)的所有根λ满足Reλ ＜0. 若不然，假设式(11)存在一个实部非负的根λ1，即Re λ1≥0.由式(11)得

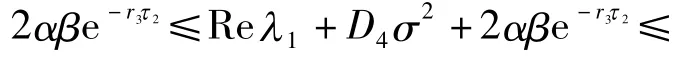
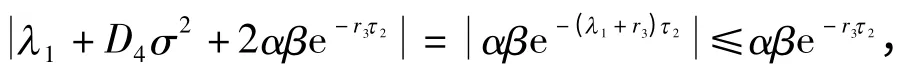
矛盾. 故式(11)的所有根λ满足Re λ ＜0.另一方面，令方程(10)的第3个因式等于零得

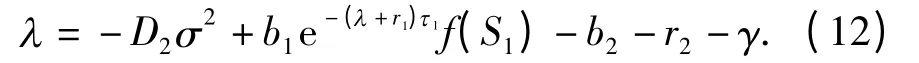
于是有下面2 种情形:

(i)若0 ＜R0＜1，下证式(12)的所有根λ满足Re λ ＜0. 否则，假设式(12)存在一个实部非负的根λ2，即Re λ2≥0. 由式(12)有

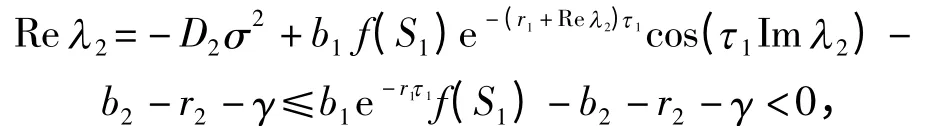
这与假设Reλ2≥0 矛盾. 故式(12)的所有根λ满足Reλ ＜0，即E1(S1，0，y1)是线性渐近稳定的.

(ii)若R0＞1，类似定理1 的证明方法可以证明E1(S1，0，y1)是线性不稳定的. □

定理3 若R0＞1，则系统(4)的正平衡点E+(S+，Ⅰ+，y+)是线性渐近稳定的.

证明 由注1 知当R0＞1 时，系统(4)有唯一的正平衡点E+(S+，Ⅰ+，y+). 在式(8)中令(S*，Ⅰ*，y*)=(S+，Ⅰ+，y+)，得到

由y+=αβe－r3τ2/r4及式(11)知方程

的所有根λ满足Reλ ＜0. 下面考虑如下方程的根:

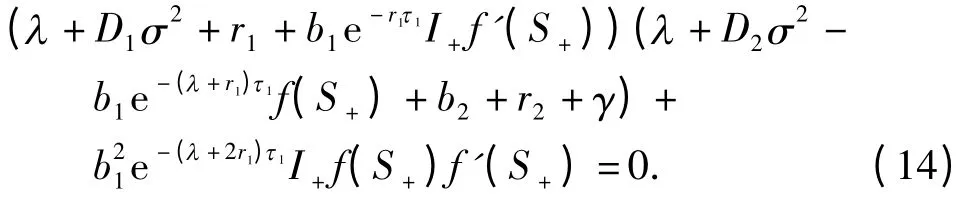
方程(14)等价于

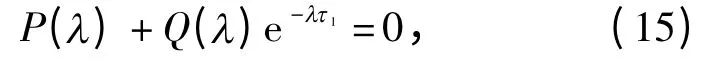
其中

对τ1≥0，有

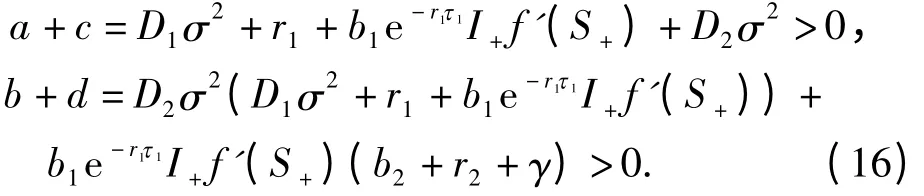
当τ1=0，方程(15)变为

由a+c ＞0，b +d ＞0 知式(17)的所有根有负实部.现需确定当τ1从0 开始递增时，方程(15)的根的实部是否会经过0 而变为正的. 可断言方程(15)没有纯虚根. 否则，假设iω (ω ＞0)是方程(15)的根，则－ω2+iaω+b+(icω+d)(cos(ωτ1)－i sin(ωτ1))=0.分离实部和虚部，得

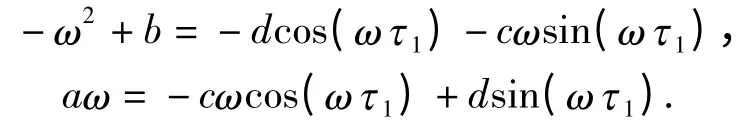
由此知道ω 满足

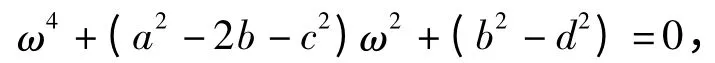
解出ω2:

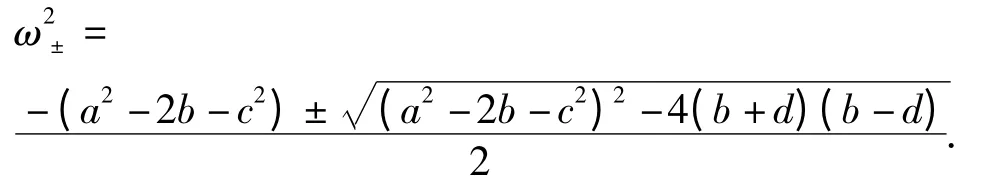
基于下面的事实:对所有的τ1＞0 有b－d ＞0，且

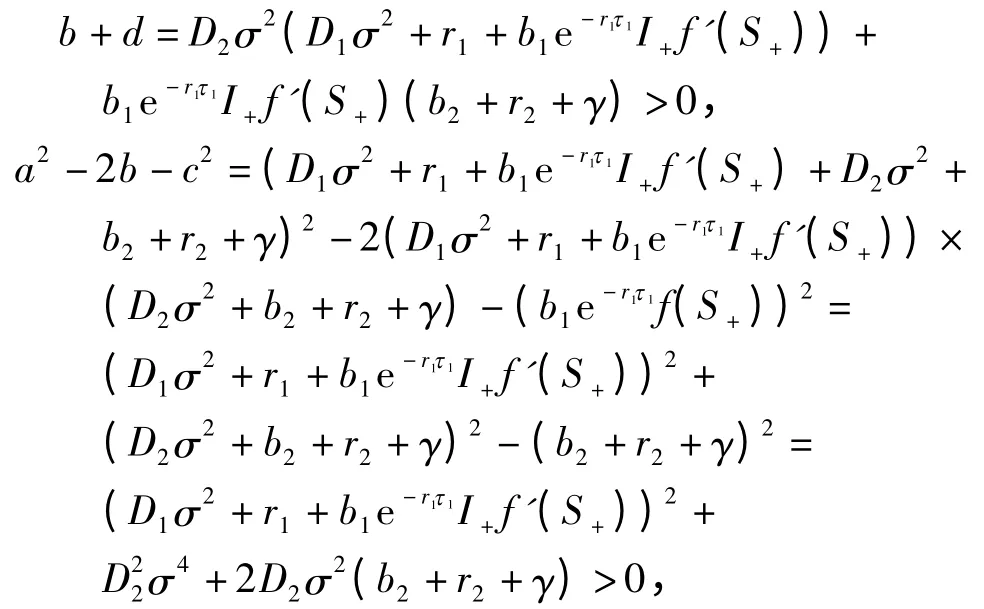
易知ω 不存在，矛盾. 故方程(15)没有纯虚根. 由Rouche 定理［12］，方程(15)的所有根也具有负实部.总结上面的讨论，可知方程(14)的所有根都具有负实部. 因此，E+(S+，Ⅰ+，y+)是线性渐近稳定的.

［1］ESTEVA L，VARGAS C. A model for dengue disease with variable human population［J］. J Math Biol，1999，38:220－240.

［2］韩博平. 生态系统稳定性:概念及其表征［J］. 华南师范大学学报:自然科学版，1994(2):37－45.

［3］KERMACK W D，MCKENDRICK A G. Contributions to the mathematical theory of epidemics［J］. Proc R Soc A，1927，115:700－721.

［4］WU Chufen，WENG Peixuan. Traveling wavefronts for a SIS epidemic model with stage structure［J］. Dyn Syst Appl，2010，19:125－145.

［5］NIE Linfei，TENG Zhidong，TORRES A. Dynamic analysis of an SIR epidemic model with state dependent pulse vaccination［J］. Nonlinear Anal－REAL，2012，4:1621－1629.

［6］ENATSU Y，MESSINA E，NAKATA Y，et al. Global dynamics of a delayed SIRS epidemic model with a wide class of nonlinear incidence rates［J］. J Appl Math Comput，2012，39:15－34.

［7］XIAO Yanni，CHEN Lansun，FRANK V D B. Dynamical behavior for a stage－structured SIR infectious disease model［J］. Nonlinear Anal－ REAL，2002，3:175－190.

［8］HONG Kai，WENG Peixuan. Stability and traveling waves of a stage－ structured predator－ prey model with Holling type－II functional response and harvesting［J］.Nonlinear Anal－REAL，2013，14:83－103.

［9］XIAO Yanni，CHEN Lansun，BOSCH F V D. Dynamical behavior for a stage－ structured SIR infectious disease model［J］. Nonlinear Anal－ REAL，2002，12:175－190.

［10］江志超，曹建涛，程广涛. 具阶段结构的多时滞SIR模型的稳定性分析［J］. 数学年刊，2011，32A(1):97－106.

［11］谢旺生，翁佩萱. 一类具有斑块扩散与反馈控制的捕食者－食饵模型周期解的存在性［J］. 华南师范大学学报:自然科学版，2012(1):42－47.

［12］陈兰荪，宋新宇，陆征一. 数学生态学模型与研究方法［M］.成都:四川科学技术出版社，2003.