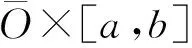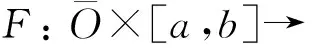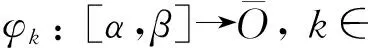含有分布导数的微分方程解的存在唯一性定理
2013-12-03杨慧敏叶国菊周雪圆
杨慧敏,叶国菊,周雪圆,周 浩,王 鸥
(河海大学 理学院,南京 210098)
0 引 言
Kurzweil[1]在Euclid空间里给出了广义常微分方程的概念,随后该概念得到了广泛应用[2-9].广义常微分方程包含普通的常微分方程和测度微分方程等[2],其解具有良好的性质,因此受到人们广泛关注[7,10-12].
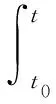
考虑区间[a,b]⊂,-∞ (1) 则函数x:O×[a,b]→n称为广义常微分方程 (2) 本文考虑如下含有分布导数的微分方程: x′=f(x,t), (3) 其中:x′表示x的分布导数;f分布Henstock-Kurzweil可积. 定义基本空间[13]为 若由D上分布的全体构成的空间是基本空间D的共轭空间,则称基本空间D上的连续线性泛函为分布或广义函数,记作D′.即若f∈D′,则f:D→,记作〈f,φ〉∈,其中φ∈D.对f∈D′,若〈f′,φ〉=-〈f,φ′〉,则称f′为f的分布导数,其中φ是检验函数.在该定义下,所有的广义函数都有各阶导数,且各阶导数都是广义函数.本文设f′表示f的分布导数,而f的普通导数记为f′(x). 设(a,b)是上的开区间,定义: D((a,b))={φ: (a,b)→且φ在(a,b)上具有紧支集}. D((a,b))的共轭空间记为D′((a,b)). 由DHK积分的定义可见,DHK积分包含Riemann积分、Lebegue积分、Henstock-Kurzweil积分及广义Denjoy积分. 分布Henstock-Kurzweil可积函数空间记作 DHK={f∈D′((a,b))|存在F∈BC,使得f=F′}. DHK的共轭空间为BV (有界变差值函数构成的空间)[14].在DHK中,若定义范数‖f‖=‖F‖∞,则DHK是Banach空间,其中F∈BC是f的原函数.在该定义下,如果f∈DHK,则对任意的φ∈D((a,b)),满足 (4) 在C([a,b])上可以定义序关系,即对u,v∈C([a,b]),u≤v当且仅当对所有的t∈[a,b]满足u(t)≤v(t).在空间DHK中,定义偏序如下:对f,g∈DHK,称fg(或g⪯f)当且仅当f-g在[a,b]上是一个正测度[10].即若f,g∈DHK,则 (5) 在上述偏序关系下,下述结论成立. 引理2[16]对于f1,f2,f3∈D′((a,b)),f1⪯f2⪯f3,若f1,f3是DHK可积的,则f2也是DHK可积的. 若当n→∞时,‖fn-f‖→0,则称序列fn⊂DHK强收敛于f∈DHK,记作fn→f. 给定r>0,记O={x∈n|‖x‖ 定义2如果函数F:Ω→n满足下列条件,则称函数F属于F(Ω,h,ω): (H1) 对任意的(x,t1),(x,t2)∈Ω,‖F(x,t2)-F(x,t1)‖≤|h(t2)-h(t1)|; (H2) 对任意的(x,t1),(x,t2),(y,t1),(y,t2)∈Ω, ‖F(x,t2)-F(x,t1)-F(y,t2)+F(y,t1)‖≤ω(‖x-y‖)|h(t2)-h(t1)|. 引理5[2]假设F:Ω→n满足条件(H1),若[α,β]⊂[a,b],x:[α,β]→n是方程(2)的解,则对任意的t1,t2∈[α,β],有 ‖x(t2)-x(t1)‖≤|h(t2)-h(t1)|. 引理6[2]假设给定F∈F(Ω,h,ω),x:[α,β]→n,[α,β]⊂[a,b],xk:[α,β]→n,如果x是函数列{xk}的极限函数,且对每个k∈,s∈[α,β],(xk(s),s)∈Ω,(x(s),s)∈Ω,DF(xk(τ),t)存在,则DF(x(τ),t)存在,且 引理7[2]给定F∈F(Ω,h,ω),且x:[α,β]→n,[α,β]⊂[a,b],xk:[α,β]→n是一列函数,如果x是{xk}的极限函数,且对任意的s∈[α,β],(x(s),s)∈Ω,则DF(x(τ),t)存在. 考虑微分方程(3),其中x′表示x∈n的分布导数. 假设[a,b]⊂,且分布f满足如下假设条件: (H3) 在[a,b]上对任意给定的x∈n,f(x,·)是DHK可积的; (H4) 在[a,b]上存在f-,f+∈DHK,使得对任意的x∈n满足f-⪯f(x,·)⪯f+; (H5) 存在连续的增函数ω:[0,∞)→,ω(0)=0和分布l∈DHK,使得对任意的t∈[a,b],x,y∈n,有 |f(x,t)-f(y,t)|⪯ω(‖x-y‖)|l(t)|. (6) 其中右侧积分表示DHK积分. (7) (8) 证明:由(H3),(H4)和式(5)有 ∀I0⊂[a,b], 因此 (10) 同理可证,当t1≥t2时,有|F(x,t2)-F(x,t1)|≤h(t1)-h(t2),因此(H1)成立. 当t1≥t2时,类似可证.因此,(H2)成立,从而结论成立. 则由(H5)可知, 定理1函数x:[α,β]→n,[α,β]⊂[a,b]是方程(3)在[α,β]上的解当且仅当x是广义常微分方程(2)的解,其中F由式(7)给出. 证明:假设x:[α,β]→n是方程(3)的解,由命题1,DF(x(τ),t)存在,且对任意的t1,t2∈[α,β],有 所以,x是方程(2)的解.反之,若x是方程(2)的解,则由命题1知,x:[α,β]→n满足式(6).又由引理5知,对任意的t1,t2∈[α,β],满足 ‖x(t2)-x(t1)‖≤|h(t2)-h(t1)|. 所以x是连续的.因此x是方程(3)的解. 引理9[2]假设F:Ω→n,F∈F(Ω,h,ω),取满足 则存在Δ-,Δ+>0,使得在区间[t0-Δ-,t0+Δ+]上存在广义常微分方程(2)的解x:[t0-Δ-,t0+Δ+]→n,且 则存在Δ-,Δ+>0,使得在区间[t0-Δ-,t0+Δ+]上存在方程(3)的解x:[t0-Δ-,t0+Δ+]→n,且满足 定义4若方程(2)的每个解y:[t0,t0+σ]→n,y(t0)=x(t0),都存在η1>0,使得对∀t∈[t0,t0+η]∩[t0,t0+σ]∩[t0,t0+η1],满足x(t)=y(t),则方程(2)的解x:[t0,t0+η]→n称为在未来是局部唯一的. 对于方程(3)可以定义相同的概念. 引理10[2]设F∈F(Ω,h1,ω1),其中h1是左连续的增函数,ω1:[0,∞)→是增函数,且当r>0时,ω1(r)>0,ω1(0)=0,对任意的u>0, (12) 定理3(唯一性) 设分布f满足条件(H3)~(H5),ω(r)>0,r>0,且对任意的u>0, (13) [1] Kurzweil J.Generalized Ordinary Differential Equations [J].Czech Math Journal,1958,83(8):360-388. [2] Schwabik.Generalized Ordinary Differential Equations [M].Singapore:World Scientific Publishing Company,1992. [3] Chew T S.On Kurzweil Generalized Ordinary Differential Equations [J].J Differential Equations,1988,76(2):286-293. [4] Federson M,Bianconi R.Linear Fredholm Integral Equations and the Integral of Kurzweil [J].J Appl Analysis,2002,8(1):83-110. [5] Federson M,Schwabik.Generalized ODE Approach to Impulsive Retarded Functional Differential Equations [J].Differential and Integral Equations,2006,19(11):1201-1234. [6] Federson M,Tboas P.Impulsive Retarded Differential Equations in Banach Space via Bochner-Lebesgue and Henstock Integrals [J].Nonlinear Anal: Theory,Methods &Applications,2002,50(3):389-407. [7] Slavík A.Dynamic Equations on Time Scales and Generalized Ordinary Differential Equations [J].J Math Anal Appl,2012,385(1):534-550. [8] Kurzweil J.Generalized Ordinary Differential Equations and Continuous Dependence on a Parameter [J].Czech Math Journal,1957,82(7):418-449. [9] Kurzweil J.Unicity of Solutions of Generalized Ordinary Differential Equations [J].Czech Math Journal,1958,83(8):502-509. [10] LU Yue-ping,YE Guo-ju,WANG Ying,et al.The Darboux Problem Involving the Distributional Henstock-Kurzweil Integral [J].Proc Edinburgh Math Soc,2012,55(1):197-205. [11] LIU Wei,YE Guo-ju,WANG Ying,et al.On Periodic Solutions for First-Order Differential Equations Involving the Distributional Henstock-Kurzweil Integral [J].Bulletin of the Australian Mathematical Society,2012,86(2):327-338. [12] WANG Ying,YE Guo-ju,LIU Wei,et al.Darboux Problem and the Distributional Henstock-Kurzweil Integral [J].Journal of Jilin University: Science Edition,2012,50(3): 452-456.(王颖,叶国菊,刘尉,等.分布Henstock-Kurzweil积分与Darboux问题 [J].吉林大学学报: 理学版,2012,50(3): 452-456.) [13] LIU Qiao-ling,YE Guo-ju.Some Problems on the Convergence of Distributional Denjoy Integral [J].Acta Mathematica Sinica: Chinese Series,2011,54(4):659-664.(刘巧玲,叶国菊.广义函数Denjoy积分的收敛性问题 [J].数学学报:中文版,2011,54(4):659-664.) [14] XUE Xiao-ping,ZHANG Bo.Properties of Set-Valued Function with Bounded Variation in Banach Space [J].Journal of Harbin Institute of Technology,1991(3): 102-107. [15] Talvila E.The Distributional Denjoy Integral [J].Real Anal Exchang,2008,33:51-82. [16] Ang D D,Schmitt K,Vy L K.A Multidimensional Analogue of the Denjoy-Perron-Henstock-Kurzweil Integral [J].Bull Belg Math Soc Simon Stevin,1997,4:355-371.
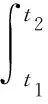
1 预备知识
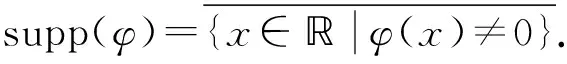




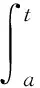
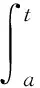

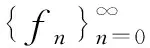
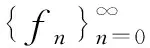
2 主要结果