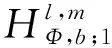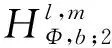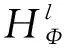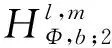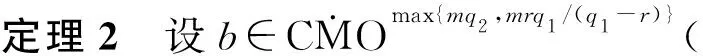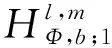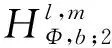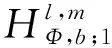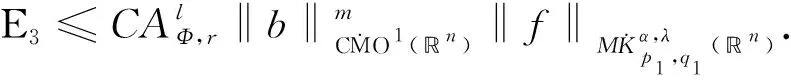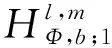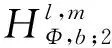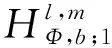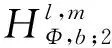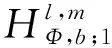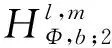n维分数次Hausdorff高阶交换子的有界性
2013-12-03任转喜陶双平
任转喜,陶双平
(西北师范大学 数学与统计学院,兰州 730070)
0 引言及预备知识
设f是n上的局部可积函数,l∈(-∞,∞),则n维分数次Hardy算子[1]为
(1)
其共轭算子为
(2)
易见,当l=0时,Hl即为高维Hardy算子:
(3)

(4)
此时算子H和H*满足
(5)
关于Hardy算子及其共轭算子的研究目前已经取得了丰富成果[2-6].实际应用中比Hardy算子更广泛的一类算子是Hausdorff算子,文献[7]研究了n维Hausdorff算子的三种推广形式,其中由Hardy算子直接推广的一种形式为
(6)
式中Φ是+上的局部可积函数.该算子及其变形的研究已引起人们广泛关注[8-10].结合分数次奇异积分算子,本文首先给出n维分数次Hausdorff算子的定义.
设f是n上的局部可积函数,0 (7) 设b为局部可积的实可测函数,m∈+,n维分数次Hausdorff算子和函数b生成的高阶交换子定义为 用B(x,r)表示n中以x为中心、r为半径的球,对于k∈,Bk=B(0,2k),Δk=BkBk-1,χk=χΔk表示集合Δk的特征函数. 定义1[12]设α∈,0 (9) 其中 (10) 定义2[12]设α∈,0 (11) 其中 (12) 当p=∞时取通常的极限情形. (13) (14) BMO(n)⊂n)⊆n)(1≤p (15) 引理1设1 证明: 利用Hölder’s不等式及极坐标变换得: 1) 若 (18) 2) 若 (19) (20) 证明: 1) 当Φ满足式(18)且α 对于Ⅰ,利用引理1中1)得 对于Ⅱ,利用引理2,有 对于Ⅱ1,利用引理1中1)及Hölder’s不等式得 对于Ⅱ2,利用引理1中1)得 因此,据Herz空间的定义得 易见 当0 当1 从而得到了1)的证明. 下面证明2).当Φ满足式(19)且α>-n(1/q-1/r′)时,有 先估计J,利用引理1中2)得 再估计JJ.利用引理2,有 对于JJ1,利用引理1中2)及Hölder’s不等式得 对于JJ2,利用引理1中2)得 因此,类似于情形1)的证明,可得到2)的证明. 最后证明3).当Φ满足式(18),(19),且-n(1/q1-1/r′)<α 由1)和2)知3)成立.证毕. 注3在定理2中若取α=0,1 证明: 本文仅给出情形1)的证明,对于情形2),类似可证.不妨设λ>0,由定理2证明中相应的估计,易得 注意到α 类似E1的估计,可得 (37) (38) 证毕. 注4同注1,在定理4条件下本文得到了分数次Hardy算子及其共轭算子高阶交换子的有界性结果. 证明: 先证情形1).当Φ满足式(18)且1/q1=1/q2+(mγ+l)/n时,利用引理3和引理1中1),并注意到α 其余证明可类似于定理2中相应的证明完成,故略. 下证情形2).当Φ满足式(19)且1/q1=1/q2+(mγ+l)/n时,利用引理3和引理1中2),并注意到α>-n(1/q2-1/r′),有 其余证明可类似于定理2中相应的方法完成,故略.证毕. 注5在定理5中若取α=0,1 证明: 证明方法类似于定理3,故略. [1] FU Zun-wei,LIU Zong-guang,LU Shang-zhen,et al.Characterization for Commutators ofn-Dimensional Fractional Hardy Operators [J].Science in China A,2007,50(10): 1418-1426. [2] FU Zun-wei,LIN Yan.λ-Central BMO Estimates for Commutators of Higher Dimensional Fractional Hardy Operators [J].Acta Mathematica Sinica: Chinese Series,2010,53(5): 925-932.(傅尊伟,林燕.高维分数次Hardy算子交换子的λ中心BMO估计 [J].数学学报: 中文版,2010,53(5): 925-932.) [3] ZHENG Qing-yu,FU Zun-wei.Lipschitz Estimates for Commutators ofn-Dimensional Fractional Hardy Operators [J].Comm Math,2009,25(3): 241-245. [4] LONG Shun-chao,WANG Jian.Commutators of Hardy Operators [J].Journal of Mathematical Analysis and Applications,2002,274(2): 626-644. [5] Sawyer E.Weighted Lebesgue and Lorentz Norm Inequalities for the Hardy Operator [J].Transactions of the American Mathematical Society,1984,281(1): 329-337. [6] FU Zun-wei,LU Shang-zhen,ZHAO Fa-you.Commutators ofn-Dimensional Rough Hardy Operators [J].Science China Mathematics,2011,54(1): 95-104. [7] CHEN Jie-cheng,FAN Da-shan,LI Jun.Hausdorff Operators on Function Spaces [J].Chinese Annals of Mathematics: Series B,2012,33(4): 537-556. [8] Liflyand E,Miyachi A.Boundedness of the Hausdorff Operators inHpSpaces,0 [9] Liflyand E.Open Problems on Hausdorff Operators [C]//Complex Analysis and Potential Theory: Proceedings of the Conference.Istanbul: [s.n.],2006: 8-14. [10] CHEN Jie-cheng,FAN Da-shan,ZHANG Chun-jie.Boundedness of Hausdorff Operators on Some Product Hardy Type Spaces [J].Appl Math J Chinese Univ,2012,27(1): 114-126. [11] GAO Gui-lian,JIA Hou-yu.Boundedness of Commutators of High-Dimensional Hausdorff Operators [J].Journal of Function Spaces and Applications,2012,2012: ID541205. [12] LU Shan-zhen,YANG Da-chun,HU Guo-en.Herz Type Spaces and Their Application [M].Beijing: Science Press,2008. [13] LU Shan-zhen,YANG Da-chun,ZHOU Zu-sheng.Sublinear Operators with Rough Kernel on Generalized Morry Spaces [J].Hokkaido Mathematical Journal,1998,27(1): 219-232. [14] LU Shan-zhen,YANG Da-chun.The Central BMO Spaces and Littlewood-Paley Operators [J].Approximation Theory and Its Applications,New Series,1995,11(3): 72-94. [15] Paluszyński M.Characterization of the Besov Spaces via the Commutator Operator of Coifman [J].Indiana University Mathematics Journal,1995,44(1): 1-18.


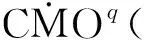
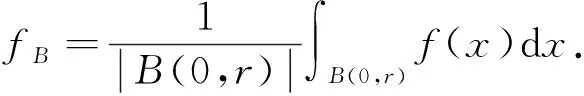

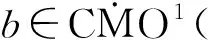
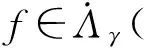
1 主要结果