不尽相同元的环排列计数问题

2013-11-23申红莲

衡水学院学报 2013年1期

申红莲

(衡水学院数学与计算机科学学院，河北衡水 053000)

1 绪论

对于n个不同元素的圆排列问题，参考线排列即可得出相应的结果，比较容易实现.文献[1-3]指出对于不尽相同元的圆排列问题，情况比较复杂，没有固定的公式可循，一般需要具体问题具体分析，但是文献[4]利用数论中的欧拉函数，给出了n个不尽相同元(有重复元素)的圆排列的计数公式.

本文主要通过举例，分析了圆排列中环排列的各种情况，利用环排列和圆排列的关系，给出了环排列的公式及其证明过程，供使用者参考.

首先给出圆排列和环排列的定义：

定义1 把n个元素按一定顺序排成一圈，就叫做这n个元素的一个圆排列，由这些元素组成的所有圆排列的个数称为这些元素的圆排列数.若这些元素不尽相同时，就叫做这n个元素的不尽相同元的圆排列.

定义2 把n个元素按一定顺序串成一个环，就叫做这些元素组成的一个环排列，由这些元素组成的环排列的个数称为这些元素的环排列数.当这n个元素互异时，又称项链问题或穿珠问题.

2 不尽相同元的环排列

环排列和圆排列之间存在着一定的联系，可参考下述例题分析.

例1 将4粒相同的白色珠子，6粒相同的红色珠子及一粒黑色珠子放在桌上，摆成一圈有几种摆法？若用线穿成珠圈又有几种不同的穿法？

解 1) 记 S = { 4.白珠,6 .红珠, 1 .黑珠} ，则11重集S做成线排列，有11!/4!6!= 2 310种摆法，由于每11个线排列对应着同一个圆排列，因此所求圆排列数有2310/11 = 2 10种.

2) 若穿成珠圈，即要求做环排列.本题中共有奇数粒珠子，其中黑珠是1粒.不妨把黑珠固定，其余10粒珠子做成的圆排列数为10 ! /4!6!= 210种.

在所有的圆排列(不妨以线排列表示)中，包含这样两种情况，为区别，以×表示白珠， O 表示红珠：

情况一：排列×O ××× ×OO×O 和 O ×OO× ×××O×其实是一个正反面的关系，因此应认定为是同一个环排列，但在圆排列的计数中，计算2次.

情况二：排列O× O ×× ××O×O两边的元素和排列位置完全相同，这样的排列可定义为对称圆排列，在圆排列的计数中计算一次，并且此类圆排列的个数为5!/2!3!= 1 0个.

综合上述2种情况，先在所有圆排列的个数中去掉对称圆排列的个数，即为情况一所示的所有圆排列的个数，除以2即为情况一中所对应的环排列的个数，情况二也是环排列的情况，需要再加上，即可得所有环排列的个数，记环排列个数为N，

例2 将4粒相同的白色珠子和4颗相同的红色珠子可以串成多少种不同花色的珠环？

解 1) 记 S = { 4.白珠 ,4 .黄珠}，则此8重集S所做的圆排列数可参考文献[3]例2有10种.

2) 若穿成珠环，即要求做环排列.本题中共有偶数粒珠子.

在所有的圆排列(不妨以线排列表示)中，包含这样2种情况，为区别，以×表示白珠，O表示红珠：

情况一：排列×O × × OO×O 和 O× O O ××O×其实是一个正反面的关系，因此应认定为同一个环排列，但在圆排列的计数中，计算2次.

情况二：排列O× O × ×O×O两边的元素和排列位置完全相同，这样的排列可定义为对称圆排列，在圆排列的计数中计算一次，并且此类圆排列的个数为4!/2!2!= 6 个.

综合上述2种情况，先在所有圆排列的个数中去掉对称圆排列的个数，即为情况一所示的所有圆排列的个数，除以2即为情况一中所对应的环排列的个数，再加上情况二所对应的环排列的个数(即对称圆排列的个数)，即为所有环排列的个数，记环排列个4数为N，

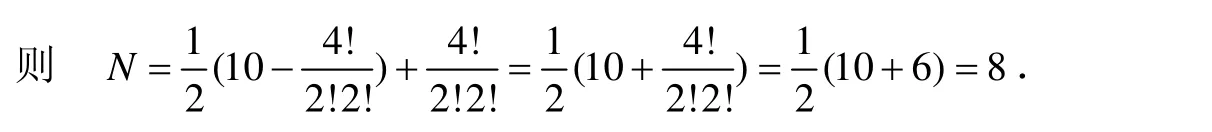
由上述2个例题可以看出，不管多重集是奇数集还是偶数集，只要分别知道圆排列和对称圆排列的个数，按照两种情况分析，则可得出环排列的计数公式.

定理1 若重集S的所有元素的圆排列个数为Q，其中对称圆排列的个数为M，则S的所有元素的环排列个数为

证明在重集S的所有元素的圆排列中，包含2种情况：第一种为非对称圆排列的前提下圆排列1翻转即为圆排列2的情况，第二种为对称圆排列的情况.去掉情况二的个数，即为情况一所示的所有圆排列的个数，除以2即为情况一中所对应的环排列的个数，再加上情况二所对应的环排列的个数(即对称圆排列的个数)，即为所有环排列的个数，记环排列个数为N，