应用Taylor公式证明相关定理

张学茂，王大增，楚建亚

(泰州师范高等专科学校 机电工程学院，江苏 泰州 225300)

Taylor公式是《数学分析》《高等数学》中一极其重要的工具，不少专家学者研究了其在求函数的近似值及误差估计、证明不等式、求函数的极限、极值、判别级数的敛散性、广义积分的敛散性、行列式的计算，乃至微分方程解等方面的应用[1-5].大多数限于一元函数问题的解决，在定理证明中的应用方面较为罕见，且笔者在长期的教学实践中发现：由于学生的知识结构与知识点编排先后的限制，许多定理、结论在首次出现时，证明的方法较繁或较抽象，给学生的理解带来了较大的困难.而学习了Taylor公式后，利用该公式可以较简易地、定性地证明相关的定理或结论，并能将一元函数的有关结论推广至多元函数，这样能加强学生对相关知识的理解，并进行有效的推广，促进学生知识结构的重组与更新.

1 预备知识

引理1[6]265-266(Taylor定理)若函数 f ( x) 在点 x0处存在 n 阶导数，则∀x∈u( x0)有

在实际应用中常用用二阶的Taylor公式

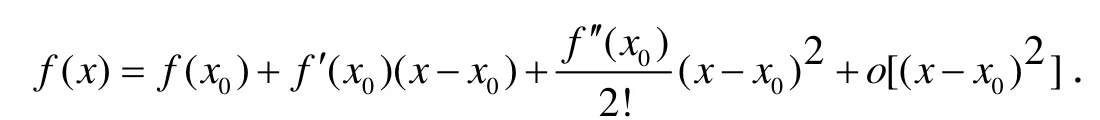
引理2[7]对于任一组不全为零的实数Δx, Δy 有则称矩阵是半正定的.

定义1[6]296f( x)为定义在区间I上的函数，对I上任两点 x ,x和实数∀λ∈（0,1）总有12f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)，则称f(x)为区间I上的凸函数，反之称为凹函数.

定义2[8]设 D ⊂ Rn是凸集，函数f( x) 定义在D 上，∀λ∈（0,1）及任意两点 p ,p∈D 恒有12 f(λ p1+(1-λ)p2)≤λf (p1)+(1-λ) f (p2)，则称 f ( x) 为 D 上的凸函数，反之称为凹函数.

定义3[6]236f( x) 为在区间I上有定义，若x∈I ，且存在 u (x)⊂I ，∀ x ∈ u ( x)总有 f ( x)≤f(x)(或0000 f( x) ＞ f( x0))，则称 x0是函数 f ( x)的极大值点(极小值点)， f (x0)是函数 f ( x )的极大值(极小值).(类似的可定义多元函数的极值).

2 证明有关的定理或结论

2.1 证明函数的凹凸性

定理 若函数 f ( x) 在区间I上二阶可导，∀x ∈I有

1) f′(x) ＞ 0则 f ( x)为区间I上的凸函数

2) f′(x)＜0 则 f ( x)为区间I上的凹函数.

证明 函数 f ( x)在区间I上二阶可导，由二阶Taylor公式取区间I上任两点 x1,x2，令x3=λx1+(1 -λ)x2，

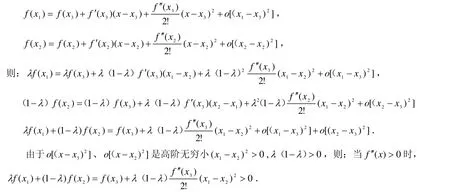
即 λf( x1)+ ( 1-λ)f(x2)＞f(x3)，f(x)为区间I上的凸函数.

当 f ′(x) ＜ 0λf(x1)+ ( 1-λ)f(x2) ＜ f(x3),f(x)为区间I上的凹函数.

笔者曾对二元函数的凹凸性等价条件作了研究[9]，利用Taylor公式还可证明多元函数的凹凸性.

定理 若函数 f(P ) 在 Rn的开凸集 D 上存在二阶连续偏导数，则对∀P∈ D ，当f(P)的Hessian矩阵半正定时，f(P)是凸函数，反之为凹函数.

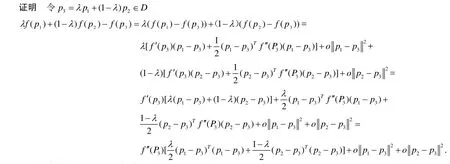
显然上式的符号由 f ′′(P3)的符号决定.

当f′(P3) ≥ 0时λf( p1)+ ( 1 - λ )f( p2) ≥ f( p3)， f ( x)是凸函数.

当f′(P3) ≤ 0时λf( p1)+ ( 1 - λ )f( p2) ≤ f( p3)， f ( x)是凹函数.

即Hessian矩阵半正定时， f ( x) 是凸函数.Hessian矩阵半负定时， f ( x)是凹函数.

2.2 证明函数的极值的第二充分条件

教材[6]281-284利用Taylor公式证明了一元函数的极值.关于多元函数的极值，我们也可利用Taylor公式来证明.

定理[10]D⊂Rn的实值函数 f ： D → R在p∈D处可微，若u( p ) ⊂ D，存在连续二阶偏导数，且

0

0 f′(p0)=0，则当 f ′(p0)半正定时， f 在 p0处取得极小值；f′(p0)半负定时，f 在 p0处取得极大值.

证明 对于 D ⊂Rn上任一点 p ，由二阶的Taylor公式得

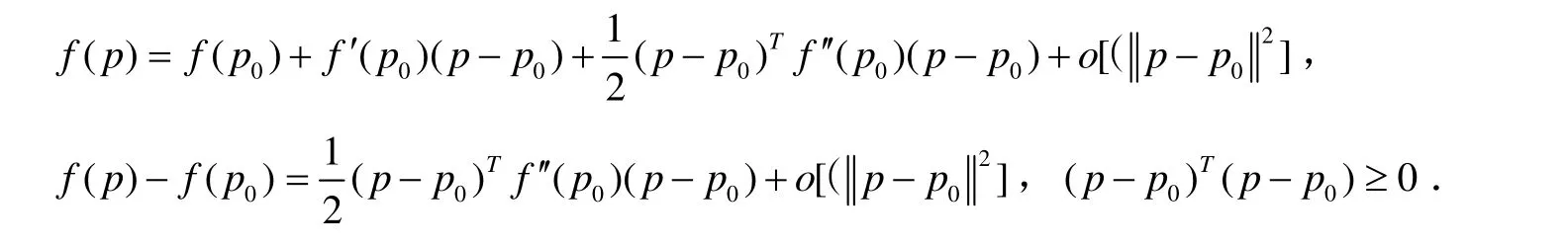
故，当 f ′′(p0)半正定时， f ( p)-f( p0) ≥ 0， f 在 p0处取得极小值；

当 f ′′(p0)半负定时， f ( p)-f( p0) ≤ 0， f 在 p0处取得极大值.

2.3 证明多元函数的Jensen不等式

2.4 对罗比达(L’Hospita1)法则的推广

求函数极限时，等价无穷小代替只运用了一阶性质，罗比达法则每次只能降低一阶，应用Taylor公式能一步到位.

定理 设 f ( x)与φ(x)为x→x0的无穷小量(或无穷大量)，且在x0邻域内可以展开成Taylor公式，x0是f( x)的 n 阶零点，x0是φ(x)的 n 阶零点，则

2.5 验证两个重要极限

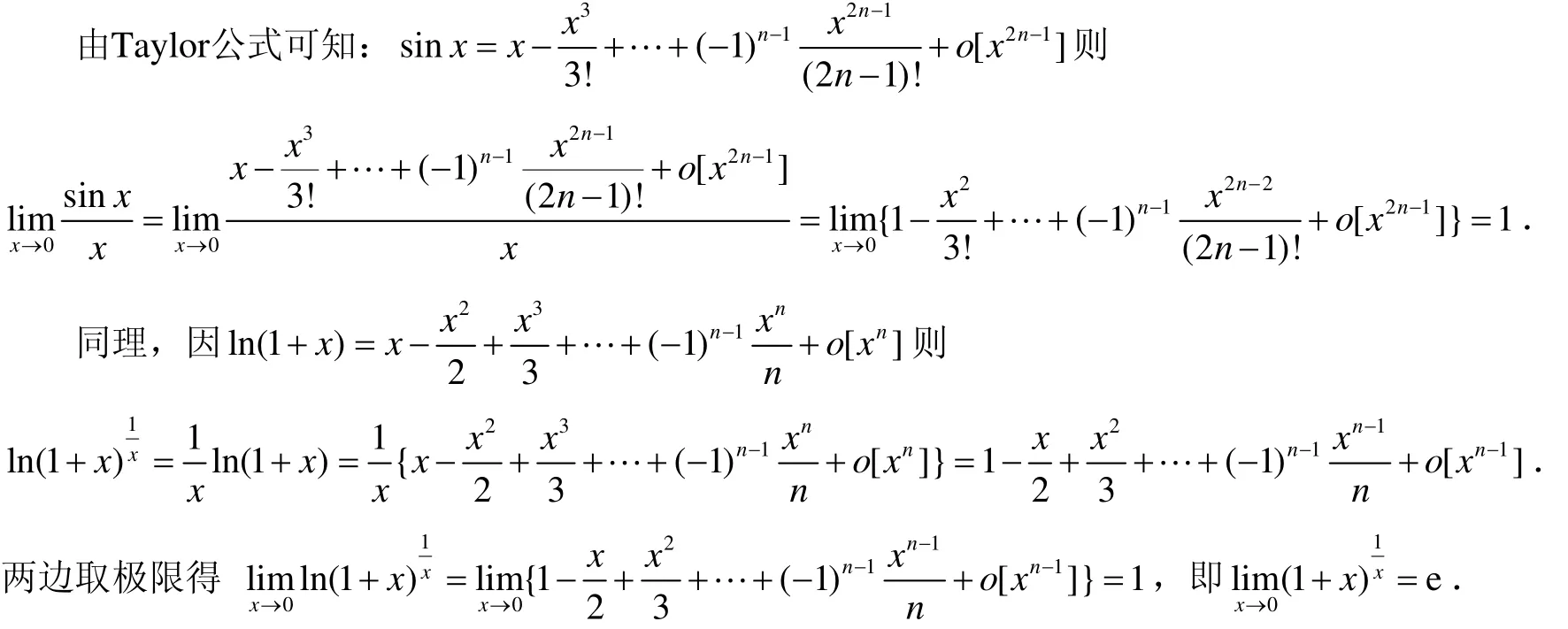
一元函数的Taylor公式、Jensen不等式等知识点出现《数学分析》上册，多元函数(重点是二元函数) Taylor公式、凹凸性、极值等出现在《数学分析》下册，且大多数教材中没有给出相关的证明和推广.我们在教学中要注重前后知识点的联系与推广，使得学生在学习中经常温习，加强整门科目各知识点的前后联系，更强调了学生在学习数学分析中不但要吃透细节，更应注重把握好各章节各知识点的区别与联系.

[1] 樊红云.函数可展开成泰勒级数的一个充分条件[J].高师理科学刊,2002(2):4-5.

[2] 谭康.泰勒公式及泰勒级数之妙用[J].高等数学研究,2010(5):11-12.

[3] 黄宗文,简灵峰.泰勒公式在讨论级数收敛性中的应用[J].玉林师范学院学报,2001(3):21-23.

[4] 邢永丽,陈建军春.泰勒级数在近似计算中的应用[J].湘潭师范学院学报,2004(3):5-8.

[5] 王三宝.泰勒公式的应用例举[J].高等函授学报,2005(6):31-33.

[6] 刘玉链,傅沛仁.数学分析讲义[M].北京:高等教育出版社,2008:236-296.

[7] 王萼芳,石生明.高等代数[M].3版.北京:高等教育出版社,2004:227-228.

[8] 米翠兰,王新春.多元函数的凹凸性的判别方法[J].唐山师范学院报,2006(9):25-26.

[9] 张学茂.二元函数的等价判别形式[J].廊坊师范学院学报:自然科学版,2011(4):18-21.

[10] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2000:242.