黄金分割比在炮口制退器结构拓扑优化中的应用

豆征,李勇,黄宏胜,张永涛

(西北机电工程研究所,陕西 咸阳 712099)

0 引言

炮口制退器是减小火炮后坐冲击的重要零件,由于侧孔气流的存在及内部火药气体压力的作用,在射击过程中不仅承受严重冲击,还要承受轴向与径向拉伸应力,因此炮口制退器必须具备合理的刚度与强度条件.炮口制退器质量太大会加剧身管振动,影响射击精度和密集度,因此炮口制退器还必须满足轻量化要求.文献[1]对复合载荷下的车体形状进行了拓扑优化,文献[2]阐述了具体几何形状的拓扑优化法则,文献[3]对桁架结构进行了拓扑优化,文献[4]对拓扑优化研究方法进行了综合阐述.

为了用尽量少的材料满足刚度与强度条件,利用有限元法对炮口制退器进行拓扑优化,在拓扑优化中引入黄金分割比,并根据综合力学性能,对比使用黄金分割比与其余比例的优劣.通过对比,发现使用黄金分割比进行拓扑优化后的炮口制退器在较小质量情况下具有较好的综合力学性能以及较大的动刚度,其分析结果对炮口制退器结构设计中降低炮口冲击的影响,在提高射击精度上具有参考意义.

1 炮口制退器拓扑优化

图1 炮口制退器

炮口制退器如图1所示.总长380 mm,内径为30 mm,外径为60 mm,锥喷管内锥角16°.所用材料的弹性模量为206 GPa,泊松比0.3,密度为7 800 kg/m3.所施加的约束条件为:左端面施加轴向约束,左端内孔壁进深60 mm范围内施加径向约束.由于炮口制退器实际受力状况十分复杂,需要运用流场力学、振动理论与非线性分析.为提高计算效率,根据炮口制退器的受力类型以及静载形变与共振形变的影响机理,对所加动载荷进行简化处理,转化为静载荷,施加载荷为:内孔壁施加25 MPa的载荷,右端外缘施加5 000 N的纵向压力,右端面施加8 000 N的拉力.所加载荷的目的是根据炮口制退器的抗弯强度、轴向抗拉强度和径向抗拉强度对其进行拓扑优化;所加载荷的依据是冲击振动引起弯曲变形、火药气体压力引起径向拉应力、侧孔后喷气体引起轴向拉应力.由于施加纵向压力只能分析一个方向的抗弯强度,而炮口制退器的振动是周向全方位的,每个方向的抗弯强度要求是一致的,所以根据拓扑优化结果还有必要进行扩展分析,对材料匹配进行合理取舍.

拓扑优化是以结构材料分布作为优化设计变量,寻求结构在给定约束情况下的最佳结构布置.拓扑优化分为连续体和离散结构拓扑优化,均是基于有限元方法,以单元相对密度为变量,确定结构中单元对整体结构的影响,决定优化后单元的去除情况.相对于尺寸优化和形状优化,拓扑优化自由度大,对减少结构质量效果显著,并且主要用于结构减重优化设计.由于机械零部件结构的多样性及零部件间相互关系的复杂性,优化单个零件结构时,不仅关注单个零件的结构特性,还要综合考虑机械零件间的相互关系,全局性地分配优化目标,达到提高整体结构特性的目的[5-6].

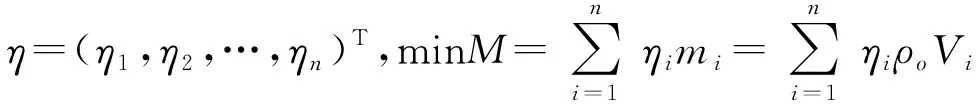
约束条件:

KT=F,μjk≤μmax,0<ηmin≤ηi≤ηmax≤1

式中:η为单元相对密度向量,M为结构总质量,mi为结构第i单元的质量,ηi为第i个单元的相对密度,n为结构单元总数,ρo为结构材料密度,K为整体刚度矩阵,T为位移矩阵,F为外部载荷,μjk为节点j在第k种工况下的位移,μmax为满足设计要求的对应节点位移,ηmin为单元设计变量的下限,ηmax为单元设计变量的上限.

图2 拓扑优化密度分布云图

选择三维实体单元SOLID95,对炮口制退器模型划分网格,建立有限元几何模型,去除材料百分比、载荷工况及收敛公差,定义优化参数，然后用拓扑优化求解器,自动执行多次迭代,对迭代结果提取密度分布云图,拓扑优化后密度分布云图如图2所示,右端锥喷管部分为非优化区域.

2 结构优化设计

2.1黄金分割比古希腊数学家欧几里德第一次用几何的方法给出了黄金分割的计算,把线段AC分为AB和BC两部分,其中AB的长小于BC的长,设AB=1,BC=x,即AC=(1+x),则AB∶BC=1∶x,而BC∶AC=x∶(1+x),如果两个比例相等,那么这条线段就是按黄金比例分割的,x的数值可以从下列二次方程式中解得:

此时,点B为线段AC的黄金分割点,0.618为黄金分割比.

黄金分割比在军事上的使用十分广泛.从马刀刃口的弧度,到子弹、炮弹、弹道导弹沿弹道飞行的顶点,从飞机进入俯冲轰炸状态的最佳投弹高度和角度,到坦克外壳设计时的最佳避弹坡度,都用到了黄金分割比[7-8].

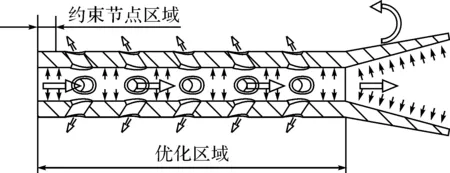
图3 优化后的炮口制退器力学模型

根据拓扑优化结果,优化后的炮口制退器力学模型如图3所示.粗箭头表示气流(火药气体)方向,细箭头表示内壁受力方向,弯曲箭头表示炮口制退器在共振情况下受到弯曲应力和扭转应力作用.

周向相邻两个侧孔在外圆面的最短弧长距离为l1,取侧孔之间凹槽的最大弧面宽度为l2=0.618l1,凹槽深度l3=0.618l2/2.

2.2判据的推导为了判断黄金分割比与其他比例在炮口制退器拓扑优化中的优劣,需要判据加以衡量.将炮口制退器左端面固定,右端受纵向力F1的作用,施加此载荷可研究炮口制退器弯曲挠度,模拟由振动引起的惯性力,此时可将炮口制退器视为简支梁,其最大挠度为δ1;炮口制退器由于侧孔后喷气流的作用而受到拉伸应力,将此力等效为右端受到的力F2,在此力作用下炮口制退器轴向拉伸量为δ2;在火药气体压力P的作用下,径向形变量为δ3.为了评价炮口制退器以较少的材料获得较好的抗弯刚度、轴向和径向抗拉强度的能力,引入参数τ,

式中,l为炮口制退器总长度,E为材料的弹性模量,I为惯性矩,A为截面积,τ表示炮口制退器综合比强度评价值,δ1、δ2、δ3分别表示炮口制退器弯曲挠度、轴向拉伸量和径向形变量[9-11],a1、a2、a3分别表示轴向拉伸量、弯曲挠度和径向形变量对射击精度及安全影响的权重系数,δ4、δ5分别表示径向两个垂直方向的形变量,m为炮口制退器质量.由τ的表达式可看出,炮口制退器的强度和刚度越高,质量越小,τ的值越大,归一化后的τ值表示炮口制退器的结构优化因数.将采用黄金分割比进行拓扑优化后的炮口制退器τ归一化后,取为1,其余为aij(i=1、2、3,j=1、2…9).归一化的步骤为:以采用黄金分割比进行拓扑优化后的炮口制退器的τ为基点,逐行逐列进行归一化.当aij<1时,黄金分割比优化成功;aij>1时,黄金分割比优化失败.根据这一判据,按照l2/l1不同比值、保留材料不同比例和2l3/l2不同比值三种情形进行研究,对每种情形都设计一系列参考比例.

图4 拓扑优化后模型的形变云图

图5 未优化模型的形变云图

2.3静强度分析与结果对比根据拓扑优化的密度分布云图,结构拓扑优化后模型的静力分析形变云图如图4所示.为了对比的需要,在与图4模型同样的长度、内径和质量的情况下,未优化的炮口制退器在静力分析后的形变云图如图5所示.炮口制退器上的凹槽在采用不同比例的情况下,优化因数的对比如图6所示,系列1表示l2/l1的情形,系列2为保留材料不同比例的各种情形,系列3为2l3/l2的情形,横坐标无量纲,表示一系列不同的比例值,如表1所示.横坐标5对应黄金分割比.从图6可看出,保留材料的比例、l2/l1和2l3/l2全部采用黄金分割比,炮口制退器的结构优化因数最高.

表1 各系列比例

为了对比图4、图5中模型的抗弯强度,在静力分析结果中设计两条中心对称且未间断的轴向路径,把分析结果映射到此路径上,然后把两条路径上对应点的形变值取平均值,其目的是获取尽可能精确的轴线上的挠度曲线,减弱炮口制退器上的侧孔特征对形变数据(挠度)造成的不利影响.在同样的长度、内径和质量的情况下,优化的和未优化的炮口制退器形变对比如图7所示.从图7可看出,优化后炮口制退器比未优化的形变量小0.22 mm.由于弯曲挠度对射击精度有直接影响,所以轴向刚度是炮口制退器拓扑优化的首要指标.

图6 优化因数对比

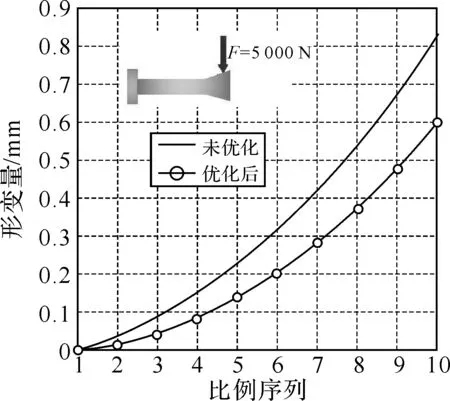
图7 形变量曲线

对优化的和未优化的炮口制退器有限元静力分析结果进行周向路径设置,然后把有限元分析数据映射到路径上.在内部火药气体压力作用下,两者的形变量如图8所示,优化后形变量为38 μm,未优化时形变量为31 μm,优化后的形变量略大于未优化时形变量.由于炮口制退器径向形变量相对弯曲挠度和拉伸形变而言,对射击精度和安全性的综合影响较小,所以炮口制退器的拓扑优化以弯曲挠度和拉伸形变为研究重点.

拉伸参数和弯曲参数对于评价值的影响如图9所示.在第二卦限、第八卦限,炮口制退器受到拉应力作用,拉应力对弯曲应力具有冲抵作用,所以拉伸参数和弯曲参数异号;在第一卦限、第七卦限,炮口制退器在有一定挠度的情况下,轴向压力使挠度加大,所以两者同号.等高线是各曲面轮廓缘线在基础坐标系上的投影,反映了自变量与因变量在三维空间的变化趋势.从第一卦限曲面图可以看出,自变量在变化域内取最小值时,因变量达到最大值.从曲面图在两个竖向基面的投影曲线可以看出,弯曲参数对评价值具有更大影响.在第二卦限、第八卦限的曲面,评价值在第二卦限有较大取值时,弯曲参数基本恒定,评价值在第八卦限有较大取值(绝对值)时,拉伸参数基本恒定.在炮口制退器受到压应力作用时(压应力仅用于考查炮口制退器的屈曲状态),评价值变化规律遵循第一卦限、第七卦限的曲面.由于第一卦限、第七卦限呈中心对称,所以只取第一卦限进行研究.从第一卦限曲面图可以看出,在极点附近较小的区域内,弯曲参数比拉伸参数的变化区间小,这说明评价值对弯曲参数具有更高的敏感度.

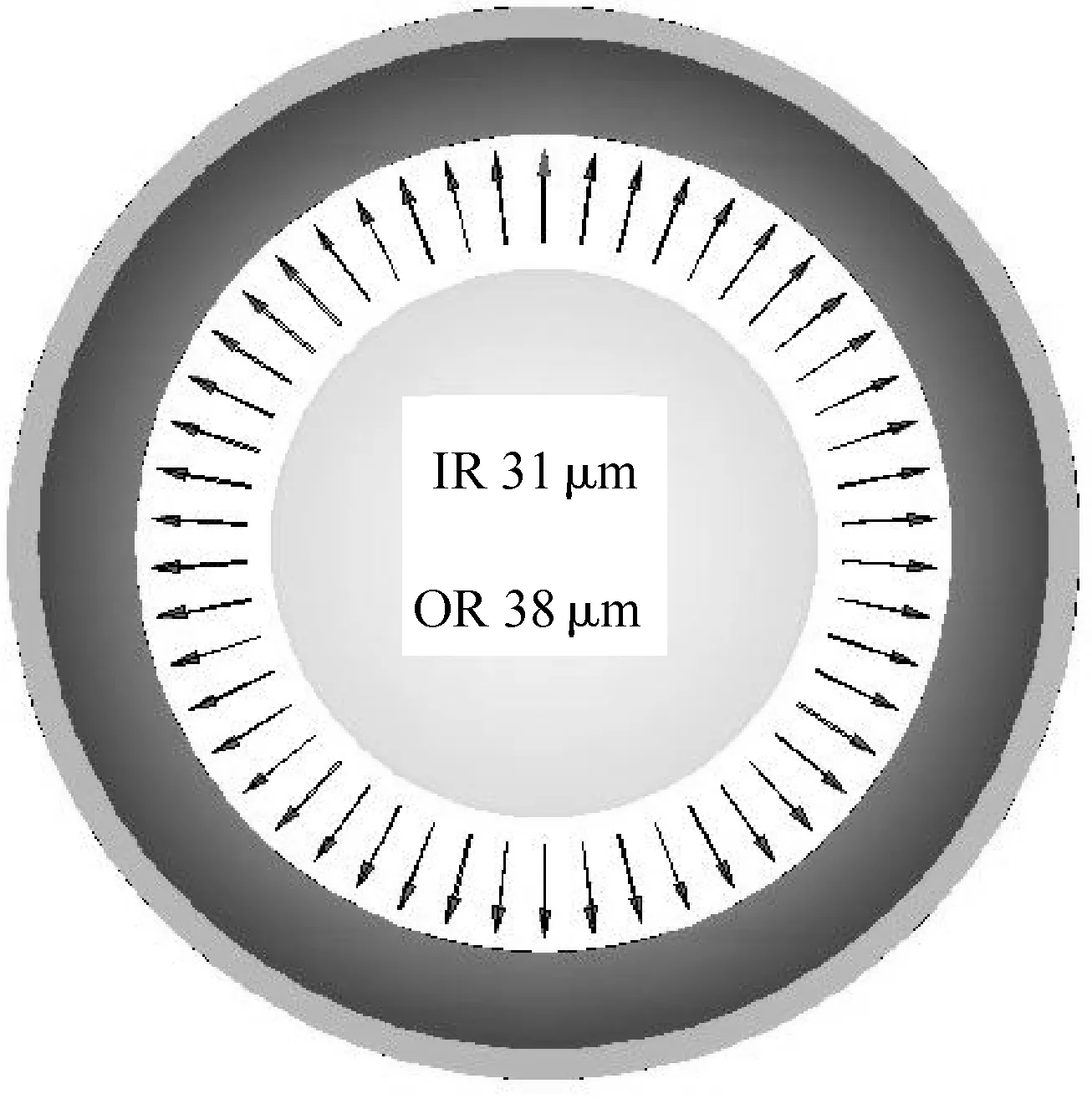
图8 径向形变示意图

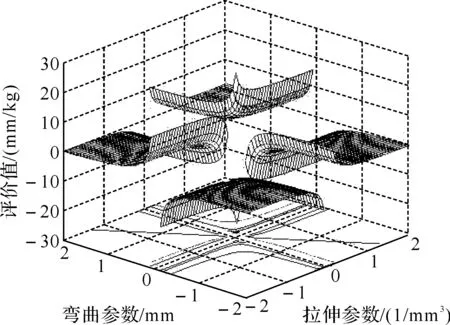
图9 评价值曲面

根据拓扑优化结果,采用黄金分割比去除材料,有限元静力分析结果为,在8 000 N轴向拉力作用下,拉伸量为6.8 μm,比在同等质量、长度和内径的情况下的未优化的炮口制退器少2.1 μm.这说明抗拉强度在优化后得以提高.

3 动刚度分析

炮口制退器在射击过程中要经受严重冲击,动刚度为物体抵制激振形变的能力.模态是物体的固有振动特性[12],通过对炮口制退器进行模态分析,在分析结果中设计轴向和周向两条路径,然后把有限元模态分析数据映射到两条路径上,对优化后与未优化的炮口制退器进行轴向路径形变量对比分析,判断优化前后炮口制退器动刚度的变化.轴向路径形变量对比如图10所示,优化后最大轴向路径形变量减小0.12 mm,说明轴向动刚度提高了.周向路径形变量对比如图11所示,优化后形变量明显下降,说明其径向动刚度也得以提高.轴向动刚度的提高,使炮口制退器的振动角位移减小,从而提高了射击精度;径向动刚度的提高,减弱了侧孔气流冲击形成的附加动载荷幅值,使炮口制退器纵向激振的影响下降.

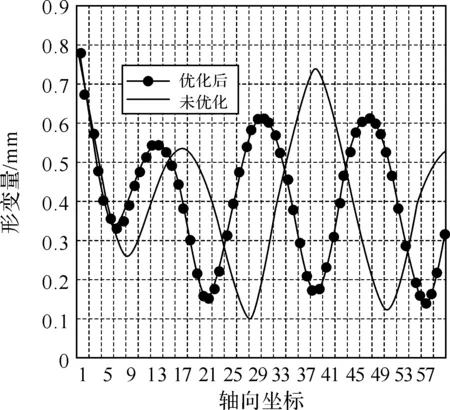
图10 轴向路径形变量对比

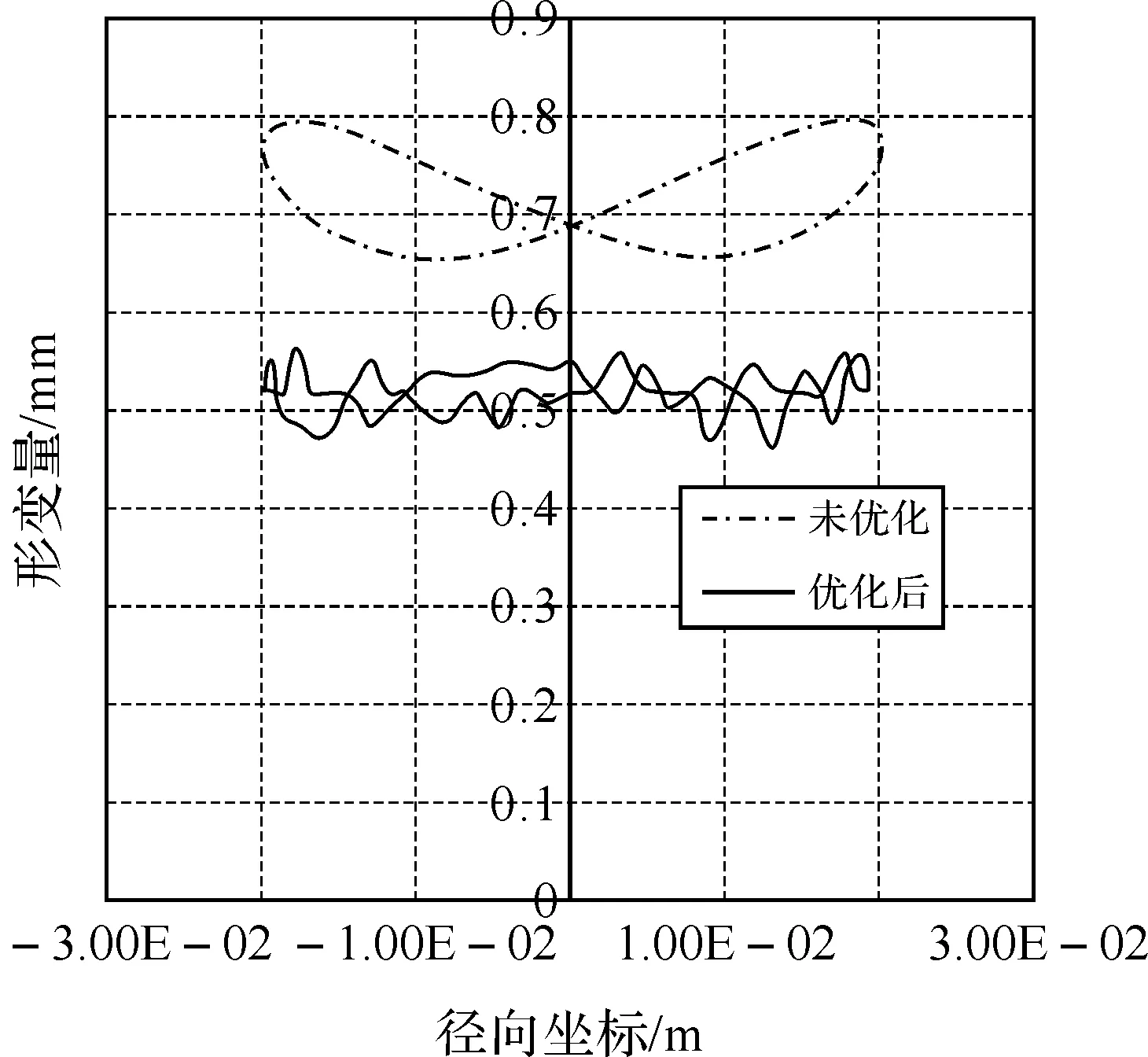
图11 周向路径形变量对比

4 结论

把黄金分割比引入炮口制退器的拓扑优化中,通过对一系列数据的分析,发现采用黄金分割比的炮口制退器具有较高的综合力学性能.对优化后的炮口制退器动刚度进行分析,结果表明,同等条件下,优化后的炮口制退器具有较大的动刚度和较小的质量.分析结果对炮口制退器结构设计及动刚度设计中满足提高射击精度的要求具有参考意义.

[1] Fukushima J. Shape and topology optimization of a car body with multiple loading condition[J]. SAE Technical Paper Series,1992,101(6):1025-1029.

[2] Roz Vany Gin, Zhou M. The DCOC algorithm, part Ⅱ: topological, geometrical and generalized shape optimization[J]. Computer Methods in Applied Mechanics and Engineering,1991,89(1-3):309-336.

[3] Bendsoe M P, Ben Tal A, Zowe J. Optimization methods for truss geometry and topology design[J]. Structural Optimization,1994,7(3):141-159.

[4] 周克民,李俊峰,李霞.结构拓扑优化研究方法综述[J].力学进展,2005,35(1):69-76.

[5] 罗震,陈立平,黄玉盈,等.连续体结构的拓扑优化设计[J].力学进展,2004,34(4):463-476.

[6] Cheng G D, Guo X. ε-relaxed approach in structural topology optimization[J]. Structural Optimization,1997,13(4):258-266.

[7] 张雄.黄金分割的美学意义及其应用[J].陕西教育学院学报,1998,(3):31-33.

[8] 金卫国.斐波那契数列与黄金分割比例[J].高中数学教与学,2009,(12):42-43.

[9] 刘鸿文.材料力学[M].北京:高等教育出版社,2005.

[10] Gere J M, Timoshenko S P. Mechanics of materials[M]. Second SI Edition. New York: Van Nostrand Reinhold,1984.

[11] Popov E P. Mechanics of materials[M]. New York: Prentice-Hall Inc,1976.

[12] Richardson M H. Fundamentals of the discrete fourier transform, sound and vibration[M]. Cambridge: Cambridge University Press,1988.