炮口结构参数对炮口性能的影响分析
2015-12-31王立君赵俊利雷红霞李大勇殷鹏贤
王立君,赵俊利,雷红霞,刘 凯,李大勇,殷鹏贤
(中北大学 机电工程学院,山西 太原 030051)
0 引言
数值模拟方法为炮口制退器效率的计算提供了新的解决途径。基于炮口流场模拟可以求解具有各种复杂形状的炮口制退器的效率,突破了传统方法只能求解特殊结构炮口制退器效率且计算公式比较繁琐等限制,而且可以得到在运动弹丸影响下的炮口超压场分布和炮口制退器受力情况,现已成为计算炮口制退器效率的主要手段。采用流场数值模拟方法来研究炮口流场比较接近实际,且流场信息更加全面、直观,计算过程更显方便,同时更有助于炮口制退器的设计。
1 计算模型说明
1.1 模型简化
依照实际情况,对炮口制退器进行如下简化:①建立的炮口制退器计算模型只有一个侧孔及挡板;②火炮身管与炮口制退器内径相等。最终得到炮口制退器的二维简化模型如图1所示,其中,A为侧孔倾角,B为挡板角度。
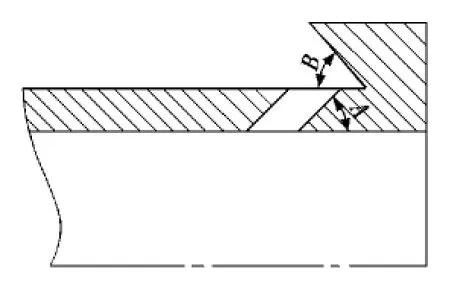
图1 炮口制退器的二维简化模型
1.2 建立计算模型
为排除干扰因素,各组炮口制退器模型的侧孔宽度、外径、总长均保持不变,A、B分别取值50°、60°、70°,两两组合总共建立9组计算模型。为方便下文描述,将以上9组模型按照“A-B”的模式依次记为“50-50”、“50-60”、“50-70”、“60-50”、“60-60”、“60-70”、“70-50”、“70-60”、“70-70”。
在炮口制退器周围建立流场计算区域,各组模型的边界条件设置保持一致,炮口制退器二维流场计算模型如图2所示。
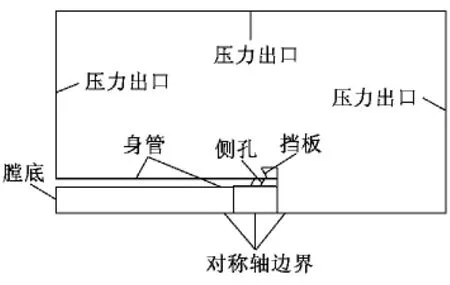
图2 炮口制退器二维流场计算模型
2 炮口制退器性能评价
2.1 炮口制退器效率计算方法
首先通过对后效期运动弹丸影响下的膛内火药气体排空的数值模拟,对不带和带炮口制退器的身管受力进行监测,得到炮膛合力随时间的变化曲线;然后将受力曲线对时间进行积分得到后效期身管所受炮膛合力的全冲量,根据冲量定理来计算身管最终的自由后坐速度;最后根据炮口制退器效率的定义,利用下式计算其效率:

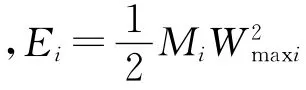
2.1.1 后效期开始时身管自由后坐速度的计算
内弹道过程中,对于自由后坐运动的弹丸、装药和后坐部分组成的系统而言,由于没有后坐阻力的作用,而且火药气体的作用力为内力,系统在炮膛轴线方向上所受外力之和为零,则满足在该方向上的动量守恒。根据动量守恒定理可得内弹道时期身管自由后坐速度W为:
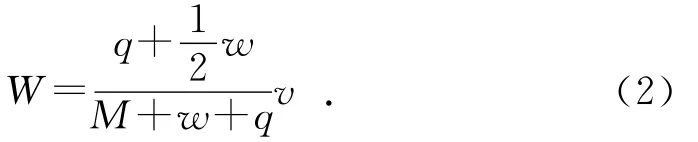
其中:v为内弹道时期弹丸运动速度;q为弹丸质量;w为火药质量。
内弹道结束的时刻就是后效期开始的时刻,由式(1)可知后效期开始时身管的自由后坐速度Wi为:

其中:vg为弹丸出炮口时的速度。
2.1.2 后效期结束时身管最大自由后坐速度的计算根据动量定理,后效期内任意时刻的后坐部分动能的增量等于炮膛合力的冲量,即:
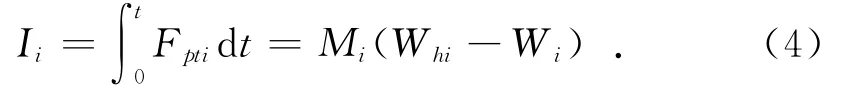
其中:Ii、Whi分别为后效期内任意时刻的炮膛合力冲量和身管自由后坐速度;Fpti为后效期内任意时刻合力。由此可得后效期内身管的自由后坐速度Whi为:
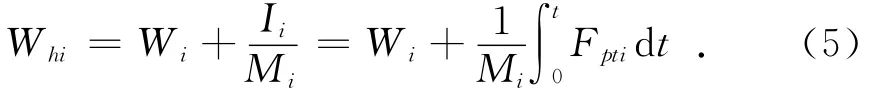
由式(5)可得后效期结束时身管的最大自由后坐速度Wmaxi为:
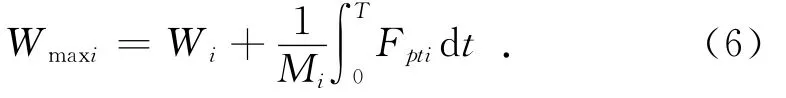
其中:T为后效期结束的时间。
将后效期结束时身管的最大自由后坐速度Wmax0和Wmax1代入式(1)即可计算出炮口制退器的能量效率。
2.2 仿真分析及计算结果
(1)选择侧孔倾角为50°,挡板角度依次为50°、60°、70°进行仿真分析。当侧孔倾角为50°、挡板角度为50°时,流场计算监测的炮口制退器合力如图3所示。将图3中的合力曲线对时间积分,可以得到炮口制退器所受合力的冲量I=4 164.374 1N·s,进而计算出该模型炮口制退器效率η=12.981 250 5%。
当侧孔倾角为50°、挡板角度为60°时,流场计算监测的炮口制退器合力如图4所示。同理,得到炮口制退器所受合力的冲量I=4 455.320 4N·s,进而计算出该模型炮口制退器效率η=11.010 730 2%。
当侧孔倾角为50°、挡板角度为70°时,流场计算监测的炮口制退器合力如图5所示。同理,得到炮口制退器所受合力的冲量I=4 672.255 6N·s,进而计算出该模型炮口制退器效率η=9.527 114 4%。
(2)选择侧孔倾角为60°,挡板角度依次为50°、60°、70°进行仿真分析。当侧孔倾角为60°,挡板角度为50°时,流场计算监测的炮口制退器合力如图6所示。同理,得到炮口制退器所受合力的冲量I=4 298.875 3N·s,进而计算出该模型炮口制退器效率η=11.713 843 1%。

图3 50-50炮口制退器合力随时间变化曲线

图4 50-60炮口制退器合力随时间变化曲线
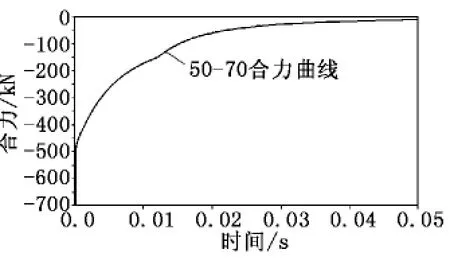
图5 50-70炮口制退器受力随时间变化曲线
当侧孔倾角为60°、挡板角度为60°时,流场计算监测的炮口制退器合力如图7所示。同理,得到炮口制退器所受合力的冲量I=4 652.350 7N·s,进而计算出该模型炮口制退器效率η=9.663 754 7%。
当侧孔倾角为60°、挡板角度为70°时,流场计算监测的炮口制退器合力如图8所示。同理,得到炮口制退器所受合力的冲量I=4 830.500 8N·s,进而计算出该模型炮口制退器效率η=8.744 989 3%。
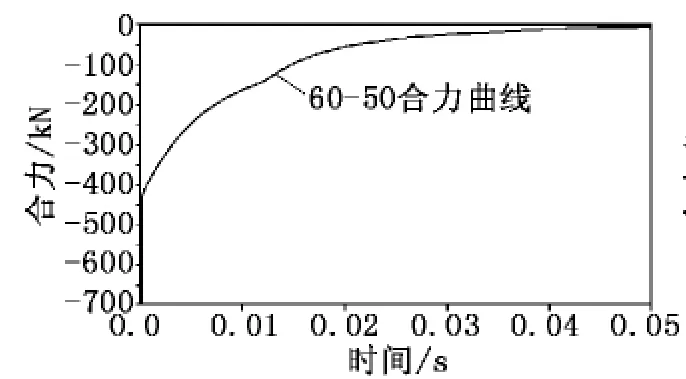
图6 60-50炮口制退器受力随时间变化曲线
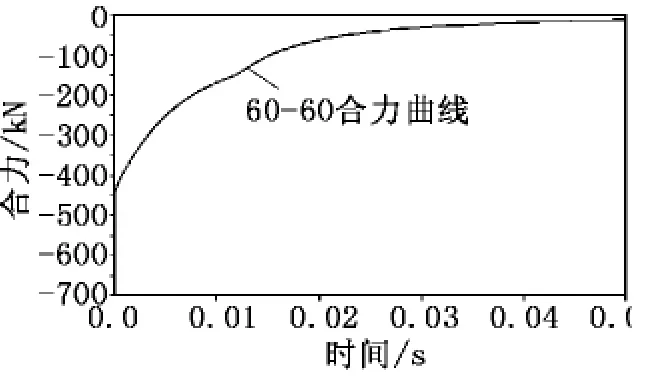
图7 60-60炮口制退器合力随时间变化曲线
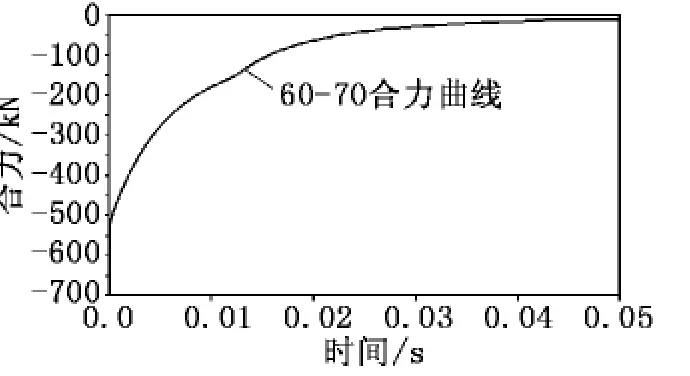
图8 60-70炮口制退器受力随时间变化曲线
(3)选择侧孔倾角为70°,挡板角度依次为50°、60°、70°进行仿真分析。当侧孔倾角为70°,挡板角度为50°时,流场计算监测的炮口制退器合力如图9所示。同理,得到炮口制退器所受合力的冲量I=4 393.840 4N·s,进而计算出该模型炮口制退器效率η=11.428 960 2%。
当侧孔倾角为70°、挡板角度为60°时,流场计算监测的炮口制退器合力如图10所示。同理,得到炮口制退器所受合力的冲量I=4 709.195 8N·s,进而计算出该模型炮口制退器效率η=9.273 259%。
当侧孔倾角为70°、挡板角度为70°时,流场计算监测的炮口制退器合力如图11所示。同理,得到炮口制退器所受合力的冲量I=4 913.344 6N·s,进而计 算出该模型炮口制退器效率η=7.863 921 6%。

图9 70-50炮口制退器受力随时间变化曲线
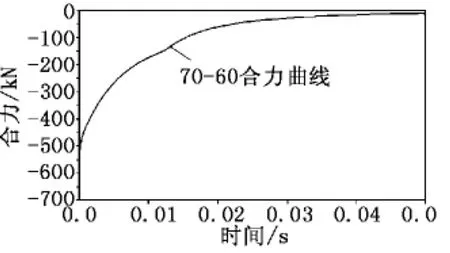
图10 70-60炮口制退器合力随时间变化曲线
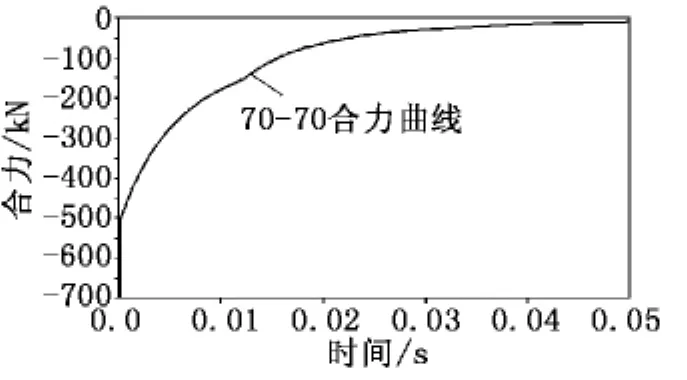
图11 70-70炮口制退器受力随时间变化曲线
将以上计算结果汇总得到不同侧孔及挡板角度对应的炮口制退器效率,见表1。
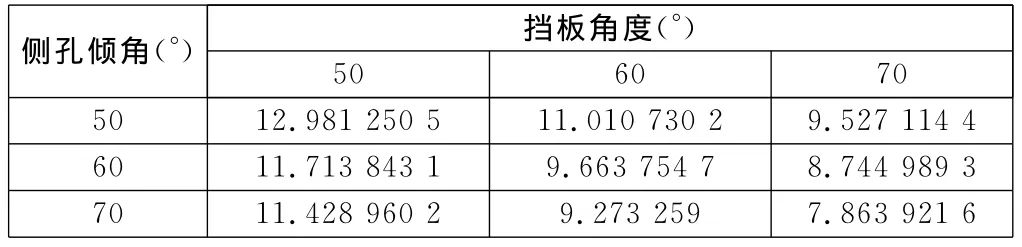
表1 不同侧孔倾角及挡板角度对应的炮口制退器效率%
3 结论
(1)当炮口制退器的挡板角度及侧孔倾角均为50°时,炮口制退器的效率最高。
(2)当炮口制退器的挡板角度及侧孔倾角均为70°时,炮口制退器的效率最低。
(3)炮口制退器效率随着挡板角度和侧孔倾角的增大而减小,挡板角度较侧孔倾角对炮口制退器效率的影响作用更显著。
[1]谭中林.基于CFD的低冲击波炮口制退器研究[D].南京:南京理工大学,2009:20-38.
[2]李鸿志,尤国钊.炮口冲击波的形成和分布规律以及对减小冲击波途径的分析[J].华东工程学院学报,1977(1):26-48.
[3]李鸿志.炮口装置受力与效率计算[J].华东工程学院学报,1984(3):1-17.
[4]王仕松,郑坚,贾长治,等.带制退器的膛口流场数值模拟[J].火力与指挥控制,2011,36(2):148-151.
