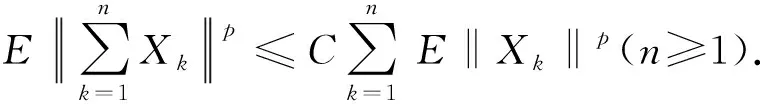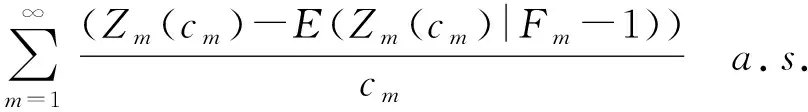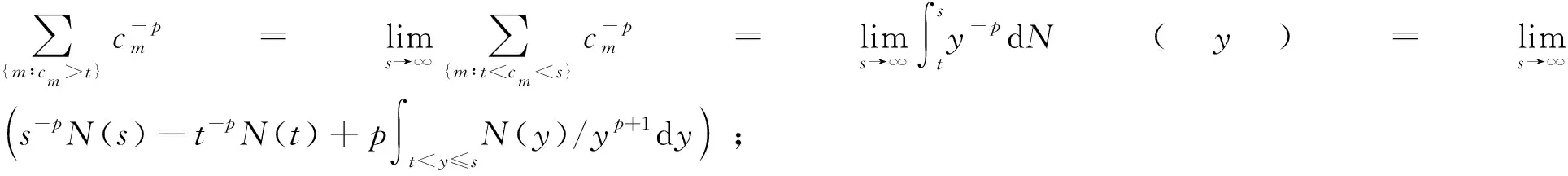B值适应可积序列加权和的强收敛性

万成高,万英

(湖北大学数学与计算机科学学院,湖北 武汉 430062)

设B是实可分的Banach空间,‖·‖表示B中的范数.(Ω,F,P)是一个完备的概率空间,{Fn,n≥1}是F的单调不降的子σ-代数序列.如果没有特别申明,本文中所言及的极限、可测、积分、期望均指强极限(依范数收敛)、强可测、强积分(Bochner积分)、强期望(Bochner积分意义下的期望).称{Xn,Fn,n≥1}是B值适应可积序列,若Xn关于Fn可测且Xn可积(n≥1).为叙述简洁,常省去几乎意义下成立的等式或不等式的标记“a.s.”.约定F0={φ,Ω},X0≡0,infφ=∞.对B值适应可积序列{Xn,Fn,n≥1}及a>0,本文中恒记Yn(a)=XnI{‖Xn‖≤a},Zn(a)=XnI{‖Xn‖>a},n≥1.

称B值随机变量序列{Xn,n≥1}是尾概率一致有界的,若存在非负的随机变量V及正常数C,使对任意的x及n≥1,都有

P(‖Xn‖>x)≤CP(V>x)

成立,此时记为{Xn}

若B是p阶一致光滑空间,对任意的1≤q≤p,B是q阶一致光滑空间.

引理1设X为B值随机变量,且对任意的x>0,都有P(‖X‖>x)≤CP(V>x),其中V为非负随机变量,C>0为常数,则对任意的x>0,q>0,有

E‖X‖qI{‖X‖≤x}≤CxqP(V>x)+CEVqI{V≤x}

有

引理2设{Xn,Fn,n≥1}是B值适应可积序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

则有

(1)

(2)

引理2的证明由于

(3)

故

(4)

即

因此

(5)

由(4)式、(5)式及Kronecker引理知(1)式、(2)式成立,引理2证毕.

定理1设B是p阶一致光滑空间,1≤p≤2,{Xn,Fn,n≥1}是B值适应可积序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

则有

(6)

(7)

定理1的证明由条件(ⅰ)、(ⅱ)及引理2知为证(6)式、(7)式成立,只须证明下列两式成立即可.

(8)

(9)

(10)

(11)

上式最后一个不等式成立基于下列事实:

推论1设B是p阶一致光滑空间,1≤p≤2,{Xn,Fn,n≥1}是B值鞅差序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

则有

(12)

(13)

推论2设B是p阶一致光滑空间,1≤p≤2,{Xn,Fn,n≥1}是B值鞅差序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

(14)

成立.

注意在推论2中若令bn=n1/r,n≥1,r>0,则有B值鞅差序列的Marcinkiewicz型强大数定律:

定理2设B是p阶一致光滑空间,1≤p≤2,{Xn,Fn,n≥1}是B值适应可积序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

则有(6)式、(7)式成立.

定理2的证明沿用定理1的证明方法,只须证明(8)式、(9)式成立即可.又由(10)式,只需证明

定理3设B是p阶一致光滑空间,1≤p≤2,{Xn,Fn,n≥1}是B值适应可积序列且{Xn}0,定义N(x)=Card{n:cn≤x},若V满足:

(ⅰ)EN(V)<∞,

则有(6)式、(7)式成立.

定理3的证明由p阶一致光滑空间的性质知

(15)

注意定理2、定理3也有类似于定理1的两个推论,这里不一一列举.

[1] Taylor R L, Hu T C. Strong law of large numbers for arrays of rowwise independent random elements[J]. Internat J Math and Math Sci,1987,10(4):805-814.

[3] Hoffmann-Jøgensen T, Pisier G. The law of large numbers an center limit theorem in Banach space[J]. Ann Probab,1976,4(4):587-599.

[4] 万成高.鞅的极限理论[M].北京:科学出版社,2002.