认知诊断DINA模型研究进展

张 潇 沙如雪

随着经典测验理论的日趋成熟和广泛应用，人们对测验的功能也提出了更高的要求。2001年，美国正式通过法案（No Child Left Behind Act of 2001，简称为NCLB），规定美国所有实施的测验应该给家长、老师及学生提供详细诊断信息，这个法案对认知诊断的研究起了巨大的推动作用[1]。传统的心理和教育测验仅以测验总分或单一的能力值作为评价指标，显得过于笼统和概括，现在人们不仅要求测验能在总的能力层面进行评价，更希望能深入到内部的认知加工的层面，为此心理学家们以认知心理学和心理测量学为理论基础，开发出了具有认知诊断功能的心理计量模型（简称为认知诊断模型，Cognitive Diagnosis Model，CDM），挖掘被试作答过程和测验分数背后的知识结构、加工技能和认知过程，做出更加准确详尽的诊断和评估，从而为采取相应的补救教学提供依据，为因材施教提供指导。

自认知诊断的概念提出以来，认知诊断模型的构建、评价和应用一直是该领域研究的热点。涂冬波和漆书青（2008）曾报告认知诊断模型已有近60种[1]，每种计量模型各具特点，比较成熟的有LLTM模型、规则空间模型、属性层次模型DINA模型以及融合模型（Fusion Model）等[1，2，4]。从研究文献来看，近十年内有大量关于DINA模型的研究。与其他模型相比，DINA模型采用了较简单的模型定义，仅涉及“失误”和“猜测”两参数，形式更为灵活，是一个简洁和易于解释的模型。尽管这个模型很简单，已被证明有很好的模型拟合（de la Torre and Douglas，2004），是现在认知诊断中的一个优良模型，在实际中的应用比较广泛，体现了较好的发展前景。

1 DINA模型的原理

DINA 模 型（Deterministic Inputs，Noisy“and”Gate Model）适用于对二元计分项目测验进行认知诊断，该模式的创建和流行始于Junker和Sijtsma（2001）的研究[4]，目前主要有de la Torre与Douglas（2004）等在进行比较前沿的研究[3，8，10，11，13，15]。

大部分CDM模型的实现都需要构建一个Q矩阵（K.Tatsuoka，1985），即一个由0和1组成的J乘K的矩阵，矩阵中的k元素表示正确回答试题j所必须的属性。这里所说的属性，可以指一种技能、一个知识点或者某种加工过程。Q矩就是构建的一个认知矩阵，这个矩阵能够明确描述回答每个试题所需要的认知过程。建立DINA模型，要首先确定测验的认知属性，建立认知属性和项目之间的Q矩阵。以de la Torre（2009）中的分数减法Q矩阵为例[3]，通过对小学分数减法运算的认知过程分析，得出掌握小学分数减法需要掌握以下五种认知属性：（1）基本的分数减法，（2）化简，（3）将整数部分与分数部分分开，（4）从整数部分借 1，（5）将整数变为分数。例如要正确作答题目，需要掌握1，3，4项属性，那么在Q矩阵中这个试题所对应的这一属性行向量为（1，0，1，1，0）。αi={αik}表征被试属性掌握模式，也可以称为被试的知识状态，k=1，2，…，K，当在第k个属性上得分为1，即 αik=1，则说明被试掌握了认知属性k，得分若为0，则说明被试没有掌握属性k。

在DINA模型中，被试的掌握模式α和Q矩阵产生了一个潜在的作答向量（a latent response rector）ηij={ ηij}，ηij是{αik}和 {qik}的函数，这个公式中，若被试i掌握了项目j考核的所有属性，则ηij=1；若被试i至少有一个项目j考核的属性未掌握，则ηij=0。如果排除失误和随机因素，对某个试题的正确作答概率只有0或1两种可能，被试的反应也仅取决于α和这个试题Q矩阵的交互作用。然而，在潜在的作答过程中肯定有猜测等成分存在，所以这个潜在作答向量仅仅代表了一种理想的反应模式。混入这个过程中的“noise”就是指“失误”和“猜测”这两个参数，也就是说，掌握了某个试题所要求的全部属性的被试可能因为失误将试题答错，而那些缺少至少一项某个试题所要求的属性的被试却有可能通过猜测正确回答了这个试题。

在DINA模型中，试题j的失误和猜测参数用分别sj和gj来定义。下面公式（1）中的Yij指被试在试题i上的反应，回答正确，则其值为1，反之值为0.

因此掌握模式为αi的被试i正确回答试题j的概率可用下面的公式计算：

在项目反应理论局部独立的假设下，DINA模型的似然函数为：

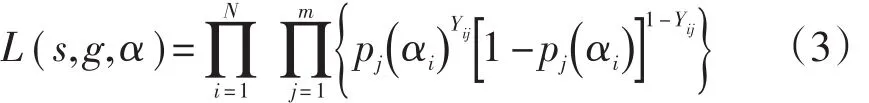
de la Torre&Douglas（2004）还指出[3]，这里所说的猜测并不是指完全随机作答，而是包含了没有反映在Q矩阵中的其他解题策略。例如，如果一个试题可以用不同的认知属性来解决，这些属性未被包含在Q矩阵中，那么具备这些属性的被试就能利用不同的策略系统地去解决问题，而并非是通过猜测答对。

2 DINA模型的改进

2.1 HO-DINA模型

在认知诊断中，α作为一种知识状态，它的每一个属性元素是对某种特定的规则或信息的掌握指标。 De la Torre&Douglas（2004）[5]认为一个能评估这些属性掌握情况的模型应该被假定这些属性与一种或几种更高层的一般智力或一般能力相联系，那些具备了高层能力（θ）的被试更有可能获得了测试项目要求的认知属性。de la Torre与Douglus（2004）把包含了θ的DINA模式就称为higher-order DINA模式（HO-DINA）。在传统DINA模型基础之上，假设在给定θ的前提下认知属性αi条件独立，则关系式可用下列式子（4）（5）表示

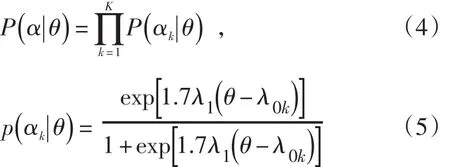
由公式可以看出，这个模型是一个包含潜在协变量θ的逻辑回归模型。它与试题反应理论（IRT）中的单参数对数模型相似，类似于一个以认知属性为项目的更高层次上的项目反应模型，λ1是指属性k的定位参数，它类似于属性掌握的难度参数，λ0k指斜率。高阶模型建立在传统模型基础上，增加了较“属性”更高阶的“能力”参数，降低了技能组合的数量，不仅能描述被试的总体水平（θ），还能描述被试对属性的掌握情况以及被试掌握属性与能力的关系，从而能够提供更丰富的信息[5]。

不管是以上提到的DINA模型，还是改进的HO-DINA模型，都是一种单策略模型，每一个项目都对应唯一的认知属性向量。而实际上，可以用多种策略对一个项目进行解答，因此，对于一个项目可以构建多个认知属性向量。多策略DINA模型[6]在单策略的DINA模型上直接进行了扩展，假设每个项目包含了能够充分解决问题的M种不同的策略，每种策略是K属性向量集合中的一个子集，可以用M个不同的矩阵表示，Q1，Q2，…，QM。对于被试i和项目j，重新定义，M，Qjkm表示QM的第j行第k列，nijm表示被试i能否用第m种策略解答项目j。检测是否至少有一种策略满足条件，一旦ηij确定之后，就可以用DINA模型中的公式进行计算了。这个模型的定义很简单，它假设s和g的值对于任何策略都是一样的，因此应用此模型的前提条件必须要求不同策略的难度要相等，这显然是有局限性的，因此如何能够允许s和g参数在不同的策略条件下变化对于多策略模型是否具有适用性至关重要，对于这个问题还需要更进一步研究。

2.2 P-DINA模型

现在已开发的认知诊断的60多种模型基本上都是适用于0-1评分数据，目前应用广泛的DINA模型模型也仅适用于0-1评分数据，而实际情境中，通过一般教育与心理测验所得的数据基本都是多级评分数据。涂冬波，蔡艳等（2010）对DINA模型进行拓广，开发出同时适合0-1评分与多级评分数据的DINA模型（简记为P-DINA模型）[7]，并采用MCMC算法实现其参数估计，同时对其性能进行研究，为认知诊断在实际中的应用提供一种新模型。

P-DINA模型DINA模型基于Samejima（1997）的等级反应模型中的累积类别反应函数思想，它的概率反应函数为：

根据项目反应理论局部独立性假设，可得出P-DINA模型的似然函数如下：

P-DINA模型下，估计的参数更多，除了0-1评分模型下要估计的α参数外，还要估计mf个失误参数s和mf个猜测参数g，涂冬波等人采用当前国际比较先进的MCMC算法来实现了此模型参数估计。经蒙特卡洛模拟实验研究表明，P-DINA模型具有良好的性能，参数估计的精度较高，若想保证属性模式判准率在80%以上，建议诊断的属性个数不宜超过7个。

2.3 G-DINA模型

DINA模式的一般化模型（Generalized DINA Model，G-DINA）由 de la Torre（2011）提出[8]，比起DINA模型，G-DINA放松了对条件的限制，它的饱和模型与基于其他连接函数的认知诊断的一般模型是等值的。在合适的限制条件下，其他一些常用的认知诊断模型都可以看成一般模型的特例。可以说，G-DINA模型为CDM提供了一个一般性的框架模型，用方程式表示：

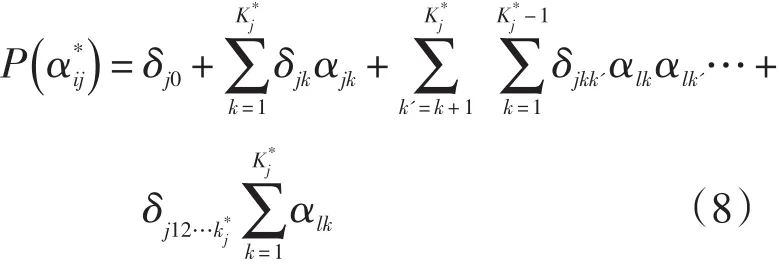
δj0为试题j的截距，表示没有掌握属性而正确回答的基线概率。δjk为对ak的主要影响，表示仅掌握了一种属性引起正确回答概率的变化。δjkk'表示αk和αk交互影响。交互影响。当均为0时，就是DINA模型了，所以DINA模型是G-DINA模型的特例。de la Torre对G-DINA的估计是采用EM算法，程序码是使用高级编程语言Ox（Doornik，2003）编写的，de la Torre指出，如果参数估计程序编码能够由更专业的程序人员用低级的语言编写出来，这将使得G-DINA模型在大规模数据处理上更加适用。

3 DINA模型的特点

DINA模型是一个随机连接模型（stochastic conjunctive model），之所以“随机”，因为被试答对项目并非由被试掌握的属性唯一决定，还加入了sj和gj，也就是说掌握了所有属性不能保证一定答对，而未掌握所考属性也不一定答错。这里的“连接”意味着所有的属性具非补偿性，被试某一属性没有掌握是不能通过其它属性来补偿，只有一个属性没有掌握和所有属性都没有掌握是一样的。DINA模型与研究得较广泛的空间规则模型一样，都要建立Q矩阵，不同的是，DINA模型不需要考虑层次间的属性关系，不是通过分类或判别方法求得被试的掌握模式，而是通过MCMC方法把它作为待估参数进行估计，这些参数包括被试的掌握模式以及sj，gj。关于参数sj和gj有两个值得注意的地方:首先模型应满足1-sj＞gj；另外在DINA模型参数估计中，要求sj和gj值不能过大，一般是不大于0.4为界限，如果超过0.4，可能说明Q矩阵界定的不好，或者是被试使用的其他解题策略，模型不拟合资料等[9]。

4 DINA模型的相关研究

4.1 模型的性能及改进研究

DINA模型在国外已经进行了相对广泛的理论研究，国内对这个模型的研究虽然不多，但是也有学者专门对此进行过探讨。一方面，很多研究着重于对该模型的改进方面，de la Torre与Douglas（2004）认为受试者的能力是多元的，应与试题难度、区分度相对应，并以此为基础提出高阶的DINA模型（Higher-order DINA模型），采用了MCMC方法对其模型进行了参数估计[5]；de la Torre（2009）还针对选择题型，提出multiple-choice DINA的模式，试图从选项中获得更多的诊断讯息，达到更精准的估计[10]。江西师范大学的涂冬波（2010）对简单的二级评分模型进行改进，提出了DINA的多级评分模型[7]。de la Torre（2011）又在传统的DINA模型基础上放松对条件的限制，提出DINA的一般化模型（G-DINA模型）[8]；另一方面，很多学者对于模型的性能也进行了大量研究，de la Torre与Douglas（2004）探讨了DINA与LLM模型的比较，得出用MCMC法对DINA的参数估计精准度较高的结论；Zhang W.M.（2006）研究了DINA模型下的DIF检测方法[9]；Rupp&Templin（2008）研究了Q 矩阵的不完整性对DINA模型诊断结果的影响[11]；Rupp&Templin（2007）和Cheng（2008）的研究表明该模型具有较高的判准率；另外，在模型的算法方面，de la Torre（2009）详述了DINA参数估计的方法，如joint maximum likelihood estimation及marginalized maximum likelihood estimation等，降低MCMC参数估计的时间[3]。由此可见，有关DINA模型的理论研究已经比较成熟，针对其缺陷改进的模型也均通过模拟和实证数据资料等证明了其诊断的可靠性以及参数估计方法的精确度，这都为DINA模型的进一步实际应用打下了基础。

4.2 模型的应用研究

近年来，在DINA模型的应用研究方面也取得了一定的进展。在测验编制和计算机自适应测验方面，Henson&Douglas（2005）提出了基于K-L信息量（Kullback-Leibler Information）在DINA模型下挑选认知诊断测验的项目或组卷研究；Finkelman&Roussos（2009）提出利用遗传算法进行自动编制认知诊断模型测验；Cheng Y.&Chang H.（2009）在DINA模型下进行了认知诊断的计算机自适应测验（CD-CAT）研究[13]。其他方面，Junker&Sijtsma（2001）用该模型来研究传递推理，Templin&Henson（2006）将这个模型用于病理性赌博的研究[2]。此外，此模型在研究儿童心理发展和学业能力测验诊断中应用较多。国内涂冬波（2009）用这个模型对项目自动生成的小学儿童数学问题解决认知诊断CAT编制进行了研究[9]。吴芳菲（2009）用该模型对六年纪学生数学评价能力评价的研究，陈艳梅（2009）用该模型对初中三年级学生阅读能力进行评价研究等。在教育测验中，应用DINA模型进行认知诊断，不但可以向家长、老师和学生等各方面提供学生的掌握模式，还能根据对试题猜对或失误的概率指导测验的编制，提高试卷质量，从而更科学准确地对学生的学业能力进行评估。

5 认知诊断DINA模型的应用前景

认知诊断作为新一代测验理论，现在已被认为是心理测量理论的核心，在过去的几年中，吸引了大批认知心理学家、统计测量学家及各专门学科专家的关注，已经成为测量研究中的热门领域，包括不断提出不同的模型以及用EM和MCMC方法对模型参数进行估计的大量研究，并在教育实践中进行了验证和初步应用。在当今教育改革的形势下，认知诊断能够为教学评价、学习障碍诊断等提供更加具体更加准确的信息，使教学目标和相应补救措施的采取更具针对性，因而已经被成功应用到了一些大规模的教育测验中。比起其他CMD模型，DINA模型不需要考虑层次间的属性关系，参数易于识别，也易于解释，是一种优良的认知诊断模型，逐渐得到了越来越多的关注和研究。但是该模型定义过于简单，对心理过程的描述不够充分，这在一定程度上限制了它在实际测验中的应用，近年来研究者们在传统DINA基础上模型上又进行了改进和扩展，出现了它的高阶模型，多级评分模型和一般模型等，尤其在与计算机自适应测验相结合方面取得了进步，相信随着理论探索的不断加深，其应用前景也将更加广阔，也必将在当前的教育和心理测量研究中发挥越来越重要的作用。

[1]涂冬波，蔡艳，戴海崎，漆书青.现代测量理论下四大认知诊断模型述评[J].心理学探新，2008，28（2）：64-68.

[2]甘媛源，余嘉元.心理测量理论的新进展：潜在分类模型[J].宁波大学学报，2008，30（6）：61-64.

[3]de la Torre，J.DINA model and parameter estimation:A didactic[J].Journal of Educational and Behavioral Statistics，2009，34:115-130.

[4]Junker B W，&Sijtsma K.Cognitive assessment models with few assumptions，and connectionswith nonparametric itemresponsetheory[J].Applied Psychological Measurement，2001，25（3）：258-272.

[5]de la Torre，J.，&Douglas，J.Higher-order latent trait models for cognitivediagnosis[J].Psychometrika.2004，69（3）：333-339.

[6]de la Torre，J.，&Douglas，J.Model evaluation and multiple strategies in cognitive diagnosis:An analysis of fraction subtraction data[J].Psychometrika，2008，73（4）:595-601.

[7]涂冬波，蔡艳，戴海琦，丁树良.一种多级评分的认知诊断模型:P-DINA 模型的开发[J].心理学报，2010，42（10）:1011-1013.

[8]de la Torre，J.The generalized DINA model framework[J].Psychometrika，2011，76（2）:179-183.

[9]涂冬波.项目自动生成的小学儿童数学问题解决认知诊断CAT编制[D].江西师范大学博士学位论文，2009:37-125.

[10]de la Torre，J.A cognitive diagnosis model for cognitively-based multiple-choice options[J].Applied Psychological Measurement，2009，33:163-183.

[11]Rupp，A.，&Templin，J.The effects of q-matrix misspecification on parameter Estimates and classification accuracy in the DINA model[J].Educational and Psychological Measurement，2008，68（1）:78-96.

[12]de la Torre，J.，&Lee.A note on the invariance of DINA model parameters.Journal of Measurements，2010，47:115-127.

[13]Cheng，Y.，&Chang，H.When cognitivediagnosis meetscomputerized adaptive testing:CD-CAT[J].Psychometrika，2009，74（4）:619-632.