一种优化数据量以提高地震速度分析精度的方法
2013-11-05郭树祥
郭树祥
(中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营 257022)
速度分析、动/静校正、叠加成像和偏移归位是地震资料处理的4大关键环节,其中速度分析占居首位且影响到其它3个环节[1]。速度的误差会造成近地表校正误差、动校正误差,以及剩余静校正量的计算误差,继而影响叠加成像的质量以及偏移的精确归位[2]。随着地震勘探的不断深入,对地震成像的精度要求越来越高,自然对速度分析精度的要求也越来越高[3]。
常用的速度分析方法多采用基于叠加能量的最小误差能量判别准则。从速度分析方法本身到所采用的判别准则都与参与速度分析的数据量有关。目前多数地震资料的覆盖次数还是比较低的;而在地表和地下地质条件复杂的地区,地震资料的信噪比也较低。对于覆盖次数和信噪比较低的地震资料,地震速度谱上的能量团发散,速度分析精度较低,尤其是中深层的精度会更低。前人采用四次项速度分析方法来增强地震叠加成像质量[4],但这种方法仅提高了中浅层的速度分析质量,还不能解决中深层速度能量发散问题。
针对中深层速度谱能量团不聚焦、速度分析精度低的问题,人们常采用多面元组合的方式来增加参与速度分析的数据量。为了进一步提高速度分析的精度,基于对速度分析数据量及数据面元大小的影响分析,通过实际地震资料的反复测试研究,笔者提出采用椭圆形面元组合方式约束远离速度分析中心点数据的方法,优化参与速度分析的数据量,以增强速度谱的能量聚焦性,提高中深层速度分析的精度。
1 速度分析精度的影响因素分析
影响地震速度分析精度的因素很多[5-8]。针对地震资料处理中如何进一步提高速度分析精度的问题,我们在这里重点分析参与速度分析的数据量及数据面元大小对速度分析精度的影响。
1.1 数据量对速度分析精度的影响
地震资料处理中多采用制作速度谱的方法来得到地震叠加速度。速度谱分析通常采用的最小能量误差判别准则如下:
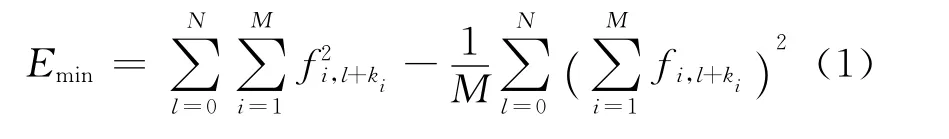
式中:M为记录道数;N为计算时窗长度;ki为第i道反射信号到达时间的采样点序号;fi,l+ki为第i记录道的第l+ki个采样点处的振幅值;Emin为最小能量误差。
当有干扰背景存在时,最小能量误差往往不明显,因此用寻找极大的等价方法来进行判别,由此衍生了平均能量、相似性系数和互相关系数等判别准则[3-4]。
平均振幅判别准则如下:
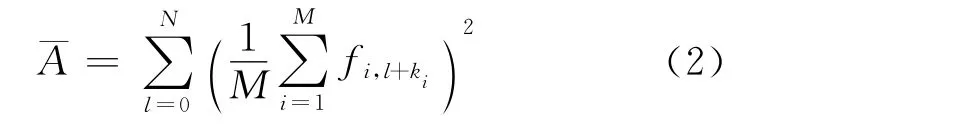
式中:括号内多项式表示对各道信号求平均,它的平方表示求平均后信号的振幅能量,对它求和表示沿反射信号时窗求总能量的和。
相似性系数判别准则如下:
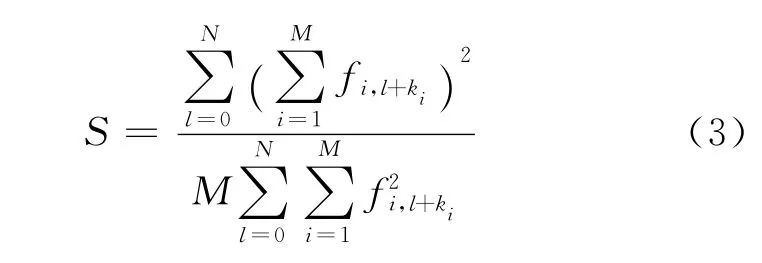
互相关系数判别准则如下:
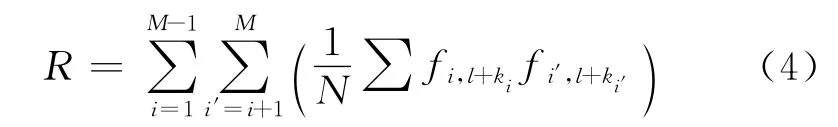
式中:i′为第i道序号加1;R为互相关系数;这里是取两个不同道的信号按括号内计算方式做互相关运算,得到相关系数后再求和。当相关系数达到最大时,就得到准确的速度值。
从上述3种实用速度判别准则来看,无论哪种判别方法都与地震道数量有关,这说明参与速度分析与判别的地震数据量(道数)起着重要作用。
1.2 常规的数据面元组合方式应用效果分析
覆盖次数较低时采集的单位面元内地震道数较少,速度分析的精度也就比较低。但目前高覆盖次数(大于80次)的地震采集相对较少,大多数的覆盖次数在80次以内,且多数老资料覆盖次数在30~60次之间。对于较低覆盖次数资料的速度分析,通常采用的方法是加大速度分析点的参与分析数据量[9]。
针对地震数据信噪比较低和面元内覆盖次数较少时速度谱能量团发散的问题,加大参与速度分析数据量的一般做法是采取多面元组合方式来扩大速度分析的数据面元。通常选用矩形或正方形的面元组合方式,这对于提高单点速度分析的质量起到了很好的作用。这里以一深层构造较复杂且信噪比不高的实际地震资料(60 次覆盖、25m×25m 面元)为例,分析采用不同组合方式扩大速度分析数据面元的实际效果。图1是3个面元3×1矩形组合(纵向3个面元,横向1排面元)和6个面元3×2矩形组合(纵向3个面元,横向2排面元)分析计算的速度谱。由图1可以明显看出,扩大速度分析数据面元后,速度谱的能量聚焦得到加强,速度分析精度得到提高。
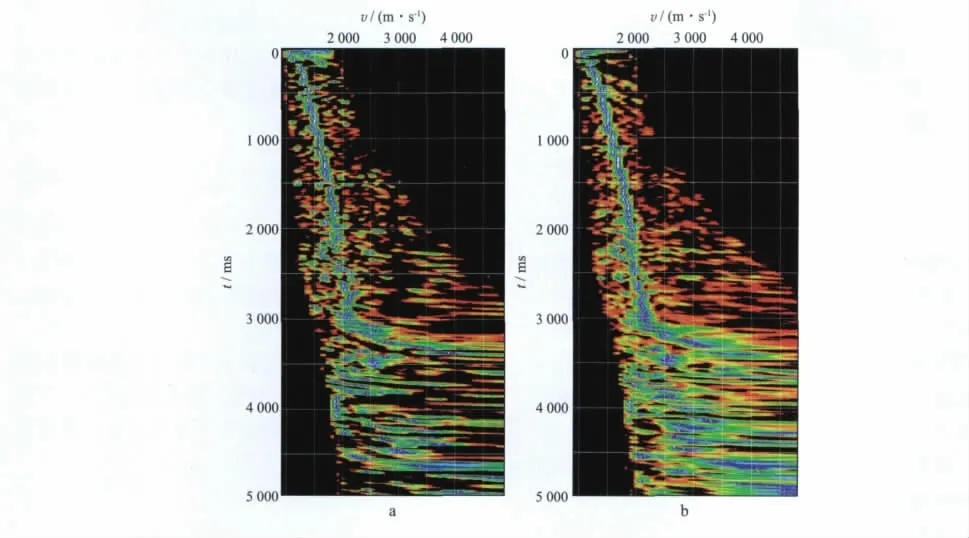
图1 3个面元3×1矩形组合(a)和6个面元3×2矩形组合(b)分析计算的速度谱
一般来讲,参与速度分析的数据量越多,速度分析的质量会越高。但是,当参与分析的数据量达到一定程度后,速度分析的质量不但不能提高,而且还会变差。分析认为,由于实际地层速度在空间上是变化的,使用过大范围的数据会使分析的速度平均化,不能反映真实的地下地层速度[7]。再说,速度分析的数据面元过大也会增加计算工作量。
速度分析的网格密度也与参与分析的面元数量有关。目前多数地震资料采集的面元网格为25m×25m,速度分析网格密度为250m×250m,有的速度分析网格密度会更小。当速度分析网格密度为250m×250m 时,两个速度分析点之间的距离为250m,即一个点的速度分析使用的数据距离跨度不能超过250m。也就是说,对于采集面元为25m×25m 的地震资料,速度分析点距离不能超过10个面元。
基于上述两个方面的分析,设计了几种数据组合进行测试。图2是分别采用3×3,5×3,7×3和7×5个面元的矩形组合分析计算的速度谱。由于参与速度分析的面元数量不同,图2中4个速度谱上能量团的聚焦程度差异很大:图2b的速度精度比图2a高;图2c的速度精度比图2b又有提高,能够达到成像对速度精度的需求;而图2d的速度精度则没有提高,且下部的能量聚焦出现了偏差,影响了深部速度的准确性。由此可见,速度分析的数据面元并非越大越好。
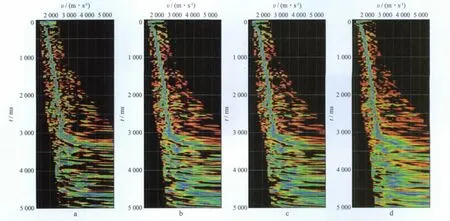
图2 3×3(a),5×3(b),7×3(c)和7×5(d)个面元矩形组合分析计算的速度谱
2 速度分析面元组合方式的优化
2.1 椭圆形速度分析面元组合方式
常规速度分析扩大数据面元的做法一般是采用矩形或正方形的面元组合方式。由于地下介质速度不是一个均匀速度场,而是一个空间变化的速度场,速度分析时扩大了数据面元,使远离速度分析中心点的数据共同参与分析,这些数据存在较大的各向异性,引起速度的聚焦性变差[10-12]。为此,基于约束远离速度分析点地震数据的考虑,通过实际地震资料的反复测试研究,笔者提出了一种优化速度分析数据量的方法——采用椭圆形速度分析面元组合方式(图3)。
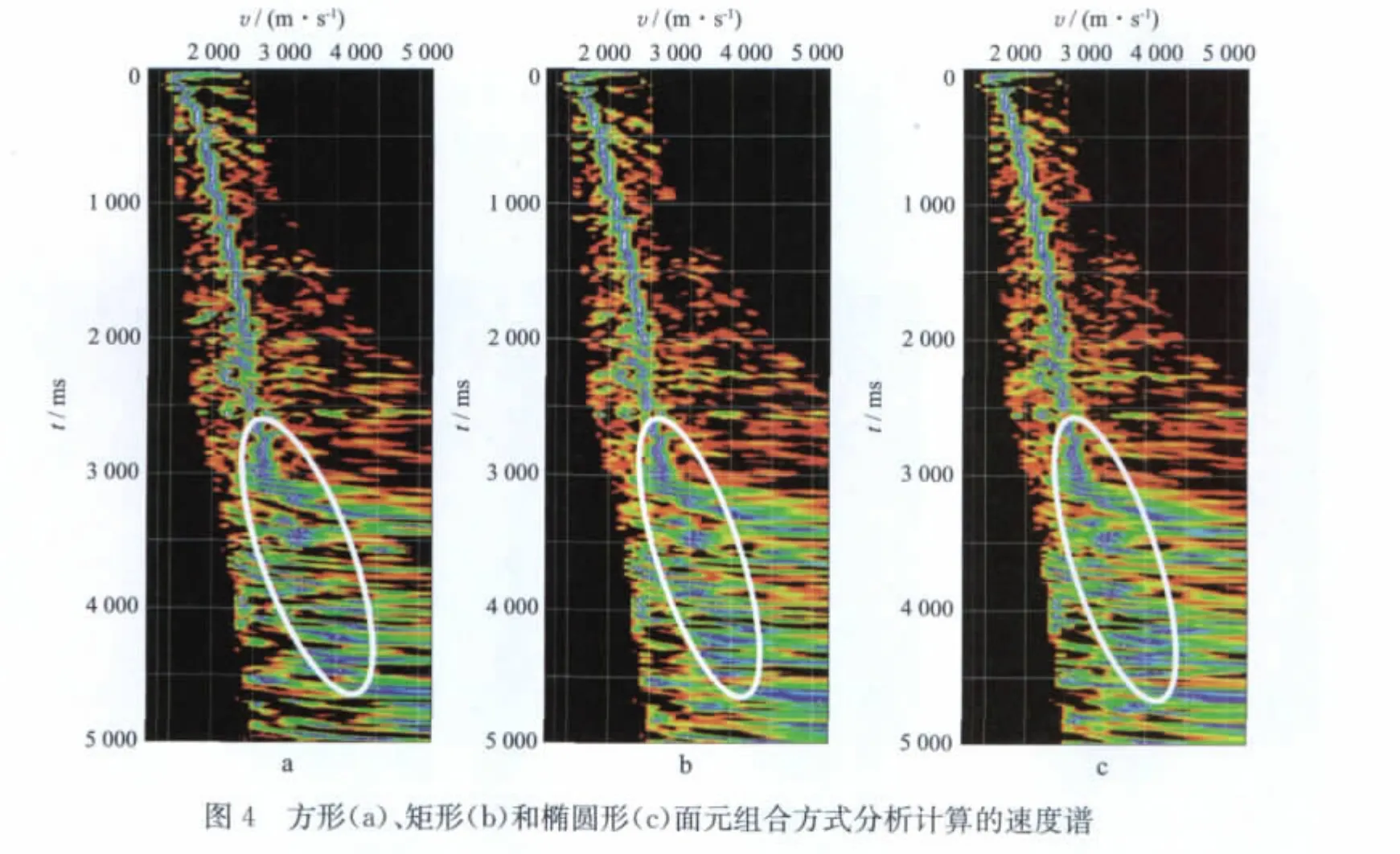
椭圆形速度分析面元组合方式既能保证参与速度分析的数据量,又约束了距离速度分析中心点较远的数据,从速度分辨率和能量聚焦性两个方面分析都比正方形或矩形的组合方式优越。图4是相同面元个数不同组合方式分析计算的速度谱。由图4可见,椭圆形组合比正方形和矩形组合分析的速度精度高,浅层的速度能量聚焦性好,深部符合速度变化趋势,能量相对集中,速度易于确定。
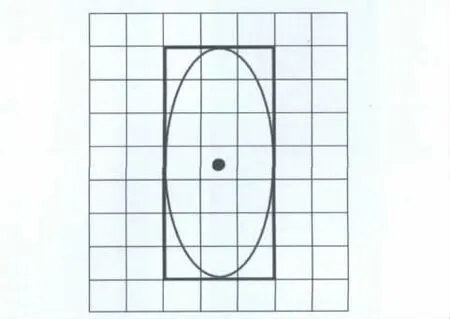
图3 矩形和椭圆形速度分析面元组合方式图解
2.2 椭圆形组合方式的面元数量分析
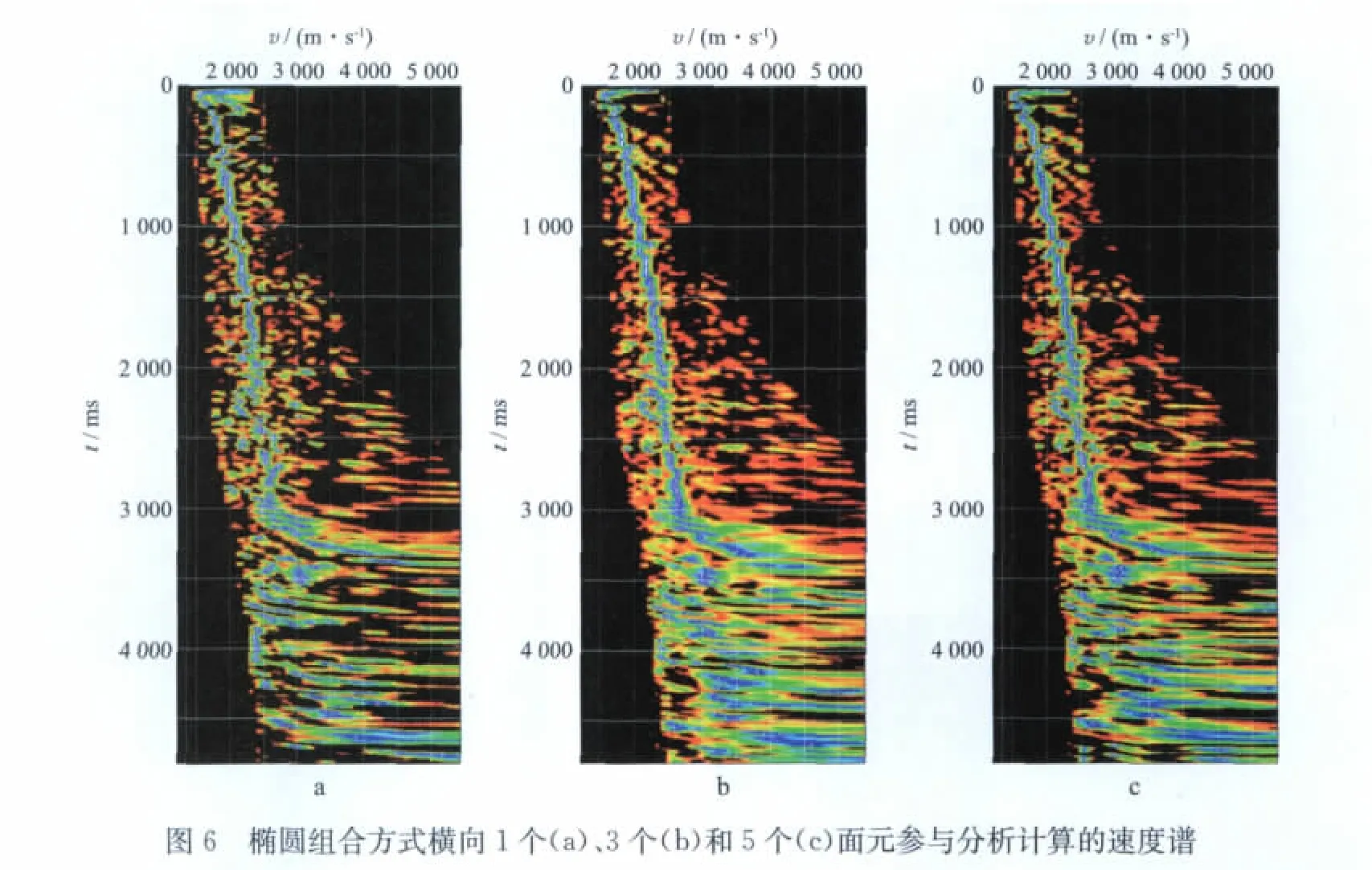
针对椭圆形组合方式纵、横向(椭圆长、短轴方向)参与速度分析面元数量的选择问题,图5给出了椭圆组合方式纵向1,3,5,7个面元分别参与分析计算的速度谱。可以看出,随着面元个数的增加,速度精度逐步提高,但到7个面元时效果变化不大,说明在纵向上参与速度分析的面元数已经到了极限。图6是椭圆组合方式横向1,3,5个面元分别参与分析计算的速度谱,可以看出,横向采用5个面元时,速度精度与采用3个面元相当,且深部有些速度点反而变得模糊了,说明横向上参与速度分析的面元数采用3个比较合适。也就是说,纵向采用5个面元,横向采用3个面元,即采用15个面元的椭圆形组合方式能够提高速度分析的精度。
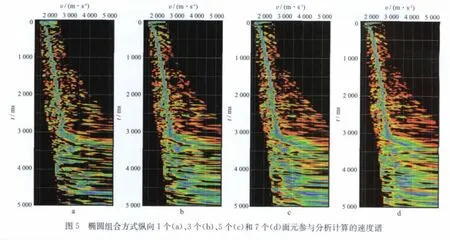
为了进一步说明这一问题,选择了另一个地区地震资料进行了测试分析。图7为采用信噪比较高的地震资料和椭圆形面元组合方式进行速度分析的结果,该地区资料采集的接收道距为25m,覆盖次数68次,接收面元为25m×50m。图7a为纵向3个面元、横向3排面元;图7b为纵向5个面元、横向3排面元;图7c为纵向7 个面元、横向3排面元参与速度分析计算的速度谱。可以看出:图7a中部速度谱能量团清晰度差,深部几个速度点没有聚焦;图7b中部速度谱能量团变得清晰,深部速度聚焦明显;而图7c中深部速度谱能量团变强,但是有些速度点的横向分辨率有所下降。由此可见,对于信噪比较高的资料,在纵向上采用7个面元参与速度分析,其数据距离速度分析中心点的跨度显得过大了。另外,从图7也可以看到,由于资料的信噪比较高,深部的一个强反射层在3张速度谱上都得到了较强的速度显示;从参与速度分析的数据量来看,对于覆盖次数和信噪比较高的资料,适当减少参与速度分析的面元个数,有利于保持速度横向分辨率。
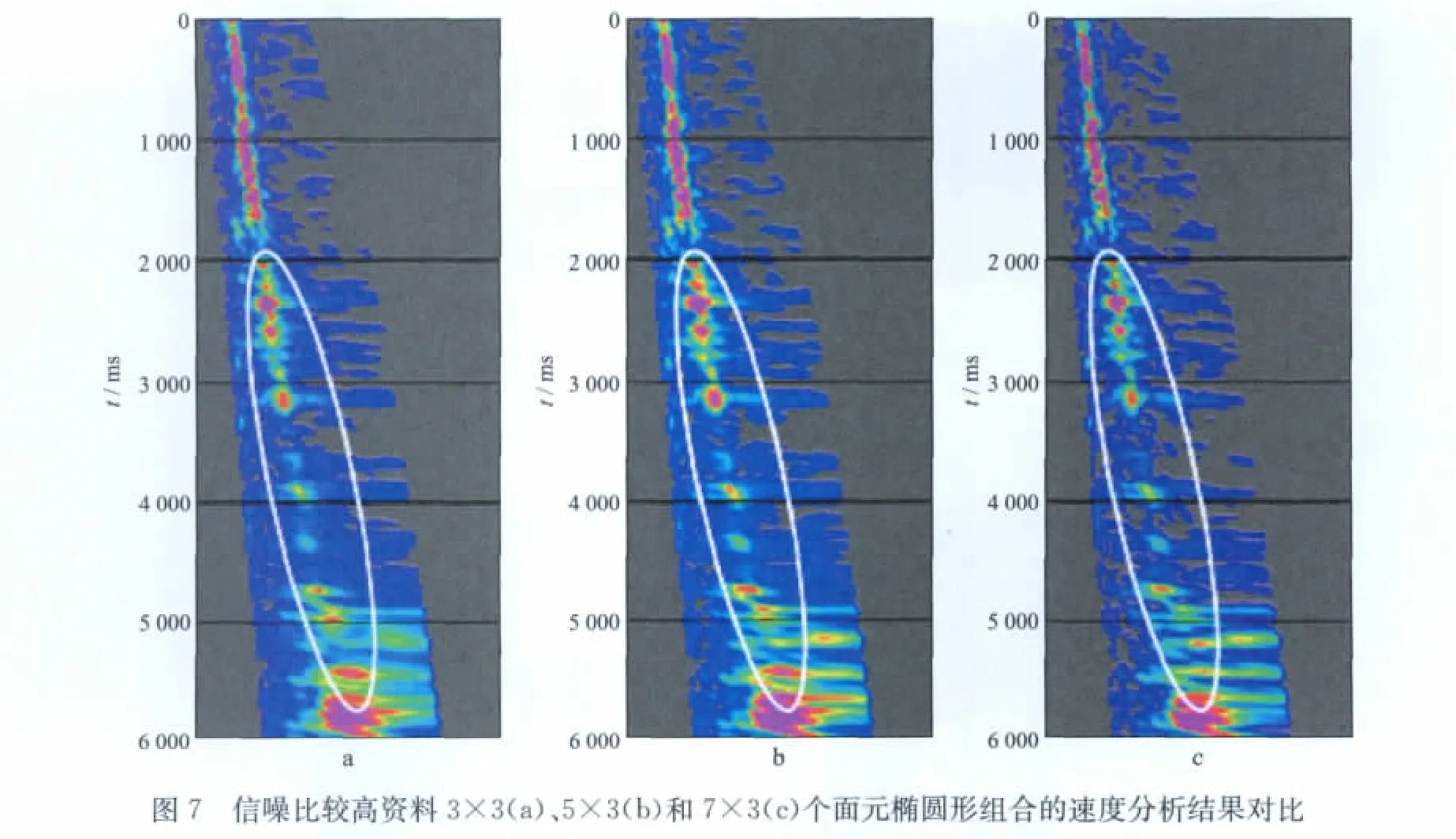
上述2个测试例子所使用的实际地震资料在覆盖次数、采集面元和信噪比上均有所不同,综合分析其速度分析效果可以得到以下认识:①参与速度分析的数据距速度分析中心点的跨度不能过大,对于椭圆形面元组合优化方式来说,一般以纵向在5个面元之内、横向在3排面元之内为佳。②所用地震资料采集面元的纵、横向尺寸相差较小或尺寸一样(如:面元25 m×25m)时,参与速度分析的横向面元个数影响小,面元的纵、横向尺寸相差较大,或者说采集面元的横向尺寸较大(如面元25 m×50m)时,参与速度分析的横向面元个数影响大。这是由于横向的数据距速度分析中心点的距离更远,对速度分析的精度有更明显的影响[13-14]。③当地震资料的覆盖次数与信噪比较高时,可以适当减小速度分析的数据量,即减少参与速度分析的面元个数,尽可能地保持速度横向分辨率[15]。
3 实际应用效果分析
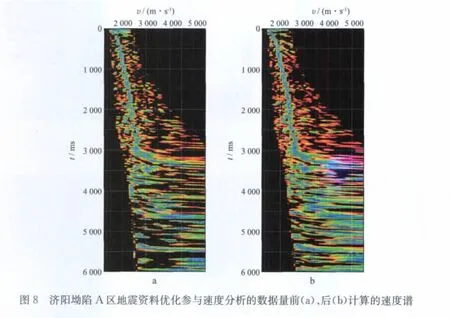
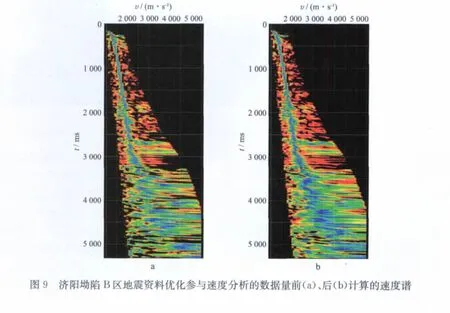
在胜利油田济阳坳陷的实际地震资料处理中,应用椭圆形面元组合方式优化参与速度分析的数据量后见到了很好的效果。图8和图9分别是A区和B 区地震资料优化数据量前、后计算的速度谱。A 区资料覆盖次数为60次,面元网格25m×25m,资料深层信噪比较低;B 区资料覆盖次数为96次,面元网格25m×50m,资料深层信噪比不高。图8a 和图9a 采用矩形面元组合,图8b 和图9b采用椭圆形面元组合,面元个数均为5×3(纵向5个面元、横向3个面元)。可以看出优化后的速度分析精度明显提高,速度点聚焦能量增强,速度趋势走向合理,深部速度谱质量明显改善,速度易于确定。图10和图11是分别对应图8,图9的叠加成像剖面,与应用优化方法前的剖面相比,应用优化后速度的叠加剖面上浅层保持了相同的地质特征,而中深层的构造成像质量得到了明显提高,波组特征关系清晰,同相轴连续性增强。尤其是图10b底部大断面成像清楚,断面下的潜山包络面及内幕地质特征显著增强,更利于后续合理的地质解释。


4 结束语
从优化参与速度分析数据量的思路出发,采用椭圆形面元组合方式约束远离速度分析中心点的数据,同时根据地震资料的覆盖次数和信噪比等因素,兼顾中深层速度能量的聚焦性和横向分辨率,合理地选择参与椭圆形组合速度分析的纵、横向面元数,能够在一定程度上提高地震速度分析的精度,特别是中深层的速度分析精度,进而提高地震成像的质量。
采用椭圆形面元组合方式优化参与速度分析数据量的方法虽然是基于胜利油田济阳坳陷陆上地震资料提出的,但从理论依据分析和实际应用效果来讲,该方法对其它地区地震资料的速度分析同样具有一定的参考和借鉴价值。
[1]牟永光,陈小宏,李国发,等.地震数据处理方法[M].北京:石油工业出版社,2007:130-142 Mou Y G,Chen X H,Li G F,et al.The method of seismic data prospecting[M].Beijing:Petroleum Industry Press,2007:130-142
[2]渥·伊尔马滋.地震资料分析[M].北京:石油工业出版社,2006:581-590 Yiermaz O.Seismic data analysis[M].Beijing:Petroleum Industry Press,2006:581-590
[3]李振春.地震成像理论与方法[M].山东:石油大学出版社,2004:123-129 Li Z C.Seismic imaging theory and method[M].Shandong:Petroleum University Press,2004:123-129
[4]郭刚明,郭树祥,李建明,等.四阶速度分析与动校正方法及应用效果分析[J].油气地质与采收率,2003,10(2):38-40 Guo G M,Guo S X,Li J M,et al.Velocity analysis and dynamic correction method and its application effect analysis[J].Geology and Oil and Gas Recovery,2003,10(2):38-40
[5]谭胜章,杜惠平,宋国良,等.高精度三维地震资料采集技术[J].石油物探,2007,47(1):74-80 Tan S Z,Du H P,Song G L,et al.High precision of three-dimensional seismic data acquisition technologies[J].Geophysical Prospecting for Petroleum,2007,47(1):74-80
[6]王西文,赵邦六.地震资料采集方式对地震处理的影响研究[J].地球物理学进展,2010,25(3):840-852 Wang X W,Zhao B L.Study on seismic processing of seismic data acquisition[J].Progress in Geophysics,2010,25(3):840-852
[7]郭树祥.高分辨率地震资料处理中的优化速度分析方法[J].石油物探,2004,43(1):80-82 Guo S X.Speed optimization in high resolution seismic data processing methods of analysis[J].Peophysical Prospecting for Petroleum,2004,43(1):80-82
[8]李振春,郭朝斌.论碳酸盐岩探区时间域速度分析[J].地球物理学进展,2011,26(2):549-556 Li Z C,Guo C B.Speed on carbonate rock formation in time domain analysis[J].Progress in Geophysics,2011,26(2):549-556
[9]郭树祥.叠前地震数据优化处理技术分析[J].石油物探,2006,45(5):497-502 Guo S X.Analysis of pre-stack seismic data optimization technology[J].Geophysical Prospecting for Petroleum,2006,45(5):497-502
[10]张军华.关于几种速度分析方法的讨论及效果分析[J].石油物探,2009,48(4):347-353 Zhang J H.Discussions on several velocity analysis method and effect analysis[J].Geophysical Prospecting for Petroleum,2009,48(4):347-353
[11]张军华.高密度资料面元细分与速度分析关系研究[J].地球物理学进展,2009,24(6):2079-2086 Zhang J H.High-density material unit of area segmentation and velocity analysis relations study[J].The Geophysics Progresses,2009,24(6):2079-2086
[12]狄帮让,熊金良,岳英,等.面元大小对地震成像分辨率的影响分析[J].石油地球物理勘探,2006,41(4):363-368 Di B R,Xiong J L,Yue Y,et al.Panel analysis of size effect on seismic imaging resolution[J].Petroleum Geophysical Exploration,2006,41(4):363-368
[13]吴国忱.各向异性介质地震波传播与成像[M].山东:石油大学出版社,2006:238-270 Wu G C.Seismic wave propagation and imaging in anisotropic media[M].Shandong:Petroleum University Press,2006:238-270
[14]彭波,郭树祥.高分辨率资料处理[J].勘探地球物理进展,2004,27(4):415-421 Peng B,Guo S X.High resolution data processing[J].Progress in Geophysical Exploration,2004,27(4):415-421
[15]王西文,刘全新,吕焕通,等.相对保幅的地震资料连片处理方法研究[J].石油物探,2006,45(2):105-120 Wang X W,Liu Q X,Lv H T,et al.Even relatively preserved-amplitude seismic data processing method[J].Geophysical Prospecting for Petroleum,2006,45(2):105-120
