多次波在采集数据缺失区地震成像中的应用研究

李宗杰，王立歆，郭书娟

（1.北京大学地球与空间科学学院，北京 100871；2.中国石油化工股份有限公司西北油田分公司勘探开发研究院，新疆乌鲁木齐 830011；3.中国石油化工股份有限公司石油物探技术研究院，江苏南京 211103）

常规地震资料处理主要利用地震一次波作为有效波来获取地下构造成像信息，其它的波场如地震多次波被视为噪声而消除，且已发展了很多衰减多次波的方法［1－7］。但有效信号和噪声的区别并不是绝对的，两者的定位标准也会随着时间的推移、需求的改变和技术的发展而有所变化。而且在复杂地区的地震勘探中，地震一次波信息的获取也会有所缺失，此时就需要挖掘利用地震资料中其它波场信息来对地震一次波成像信息的不足进行补充。本文提出利用多次波成像来补充在地震观测系统遇到障碍情况下地震一次波成像信息的不足。

从地震波传播过程来看，和一次反射波类似，多次波也是地下反射层的反射，蕴含了地层结构信息，在某些地质结构情况下，多次反射波中蕴含着一次反射波中没有的地震信息。因此，可以将多次波看作有效信息并对其进行成像。

很多学者研究了如何有效利用多次波。Reiter等［8］提出利用叠前Kirchhoff方法对深海多次波进行成像；Guitton［9］利用组合炮偏移的方法对多次波进行成像；Muijs等［10－12］结合常规一次波偏移方法，将低阶多次波（一次波视为零阶多次波）作为震源，高阶多次波作为接收记录，实现直接利用多次波记录进行成像。Shan等［13－17］基于交叉互相关偏移的方法对多次波进行成像，其基本思想是通过互相关将表层多次波重构为和一次波类似的虚拟一次波，然后采用常规一次波的成像方法进行成像。此类方法对多次波信息的利用比较灵活，因为构建的虚拟一次波数据作为中间道集，后续除了可以将多次波信息用于地震成像，还可以用于填补由于常规观测系统的限制造成的近炮检距数据的空白。如William 等［18］利用二维非稳相预测误差滤波（PEF）对虚拟一次波进行训练后用于补充缺失的近炮检距数据；Wang等［19］基于一维匹配滤波的方法对虚拟一次波进行校正后用于补充缺失的近炮检距数据。Berkhout等［20］基于全波场反演方法，实现利用多次波来获取成像信息。

上述方法都是研究利用多次波对地下结构成像，但从发展到目前的地震数据处理思路看，还是以一次波成像为主体。在此情况下，利用多次波的成像信息来弥补一次波成像信息的不足，提升最终成像剖面的完整性和准确性，也将体现出多次波信息作为有效信息的重要的应用价值。本文介绍了在仅利用地震数据中一次波信息进行成像的前提下，当地震采集过程中遇到某些障碍地段造成观测系统间断，从而引起地下目标构造成像信息缺失时，利用已有地震数据中的多次波成像信息对其进行补充的方法技术及其测试效果。

1 地震一次波成像存在的问题

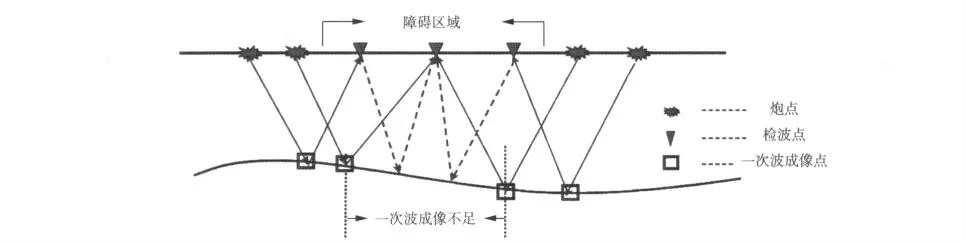
图1 由于观测系统中障碍区域导致地震一次波成像信息不足原理示意图解

2 多次波成像方法

2.1 虚拟一次波构建

将多次波降阶，是构建虚拟一次波的基本思想。虚拟一次波构建具体实现算法是，在地面对同一个炮集的原始记录和多次波记录进行互相关，然后基于参与互相关的记录道的接收点位置，将各个炮集对应的互相关结果进行叠加，即可得到新的道集。该道集和一次波具有相似的表现特征，故称为虚拟一次波记录［16］。

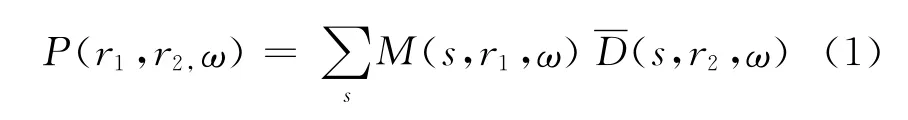
式中：ω是频率；s是震源位置；r1和r2是接收点；（s，r2，ω）是地表接收波场D（s，r2，ω）的共轭复数；M（s，r1，ω）是提取的表层多次波记录波场；P（r1，r2，ω）是拟震源在r1，拟接收点在r2的虚拟一次波场。r1和r2可以选择在任意接收位置，因此，可以构建出任意炮检距的虚拟一次波记录，甚至当r1＝r2时，可以得到实际采集中不可能得到的零炮检距记录。虚拟一次波记录可以填补实际采集数据时由于观测系统的限制而无法得到的近炮检距数据空白，利用虚拟一次波数据成像也可以弥补原始采集数据时由于近炮检距数据缺失而无法到达的照明范围。

上述方法中应用原始数据和多次波数据互相关构建虚拟一次波数据，需要将多次波场提取出来。多次波场的提取可以借鉴常规多次波压制方法中采用的SRME 方法或其它多次波压制方法中多次波预测环节采用的方法技术。

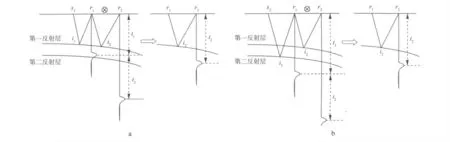
图2 虚拟一次波构建基本原理

图2给出了采用互相关方法构建虚拟一次波的基本原理。其中，在r1点接收到的一次波记录继续向下传播并经地下反射被r2接收形成表层多次波记录道。标志“○×”代表互相关，通过对r1点接收到的一次波记录和r2点接收到的多次波记录进行互相关，可以从多次波记录道中消去一次波记录道的旅行时信息，从而得到旅行时为t2（即r1→i2→r2）来自于地下反射点i2的波场信息。虽然图2a和图2b中的震源不同，但都能通过对r1接收的一次波信息和r2接收的表层多次波信息进行互相关得到相同的从r1传播经地下第一反射层反射到r2的波场信息。当基于各个炮集将对应的互相关结果进行叠加时，两者波场信息叠加构建出虚拟一次波中以r1为拟震源，r2为拟接收点的虚拟一次波记录道。因此，基于炮集将所有的一次波和其相对应的表层多次波信息互相关结果进行叠加就可得到虚拟一次波道集。此虚拟一次波道集中的反射同相轴记录的是真正的地下反射波场信息。

但是在实际利用原始记录和表层多次波记录进行互相关的过程中，并不能特定选取成对的一次波信息和相应的表层多次波信息进行互相关，而是选取整个记录道进行互相关。因此，存在有非成对的数据信息进行互相关，并在最后构建的虚拟一次波数据中表现为噪声。

2.2 局部倾斜叠加压制干涉噪声

通过对虚拟一次波形成机理进行分析，我们得出，成对的一次波和多次波互相关形成的波场是真正的地下反射波场信息，将这些互相关波场基于炮集进行对应叠加，即形成虚拟一次波记录中的同相轴；而非成对的波场互相关形成的波场都是随机变量，基于炮集进行叠加后，此类随机变量之和形成的波场无法在虚拟一次波记录中形成具有连贯性的同相轴，而是表现为背景干涉噪声。

基于这些波场特征分析，我们提出应用局部倾斜叠加变换来压制虚拟一次波数据中的背景干涉噪声，提取有效同相轴。局部倾斜叠加变换将数据体分段进行处理，将每段映射为具有不同倾角的线性倾斜轴的叠加，如公式（2）所示。

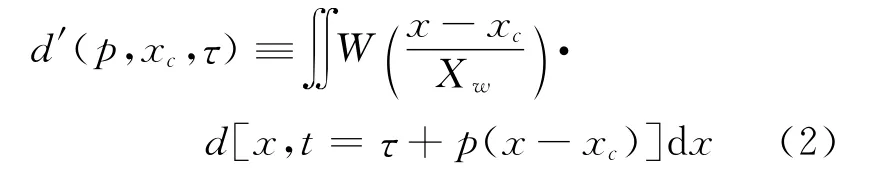
式中：W（x）为窗函数；xc为窗函数的中心；Xw为窗函数的宽度；p为射线参数，表征了窗函数截断的同相轴的斜率；τ为在x＝xc时的时间截距；d（x，t）和d′（x，t）分别为原始数据和变换域数据。

英语影视作品的在教学中的应用已经得到了诸多英语教师和研究者的重视，其优势在跨文化交际课堂也得到了充分的体现：

通过公式（2）将同相轴分段进行局部倾斜变换处理，根据分析虚拟一次波有效同相轴和干涉噪声的表现特征，窗函数内的虚拟一次波有效同相轴可以用不同斜率的线性同相轴之和来表征，但是干涉噪声则不然，此为信噪分离的关键。

在具体实现时，表征同相轴斜率的射线参数p是最外围循环变量；滑动的窗函数W（x）和时间截距τ是内部循环变量。窗函数的宽度Xw表征了可看作线性同相轴的横向道数范围，窗函数越宽需要用来表征其同相轴斜率特征的p值范围就越大。

通过逆变换公式（3）可以将数据反变换回原始数据域：

全局倾斜叠加变换是将整个剖面的同相轴假设为具有不同倾斜特征的线性同相轴进行叠加，当这个假设和实际数据不匹配时，就会引入假象噪声。而局部倾斜叠加变换是结合窗函数对同相轴分段进行变换处理，可以避免由于对整体数据过于简单化的表征带来的假象噪声。

2.3 虚拟一次波成像算法

对虚拟一次波进行去噪处理后，再对其进行偏移成像。为适应复杂的地质构造成像，我们对虚拟一次波采用带误差补偿的频率－空间域有限差分法叠前深度偏移。其波场延拓算法处理包含了3步：①频率－空间域的有限差分处理；②频率－空间域的时移处理；③频率－波数域的误差补偿处理。这种算法补偿了频率－空间域有限差分法求解时引入的误差，对介质速度横向变化剧烈的地区也有很好的适应性［21］。

3 数值试算

3.1 Sigsbee2B模型数据测试

我们基于Sigsbee2B 模型数据来检验本文方法的有效性。图3给出了Sigsbee2B 速度模型剖面；图4给出了Sigsbee2B模型数据的某单炮记录（箭头所指为多次波，可以看出多次波较发育）。图3中矩形黑色虚线框所示的部分为无法放炮、只能放置检波器接收其它炮数据的区域。利用已有炮数据包含的一次波进行偏移成像，得到的成像结果如图5所示。可以看出，由于采集的地震一次波信息缺失使得地下成像信息不完整。

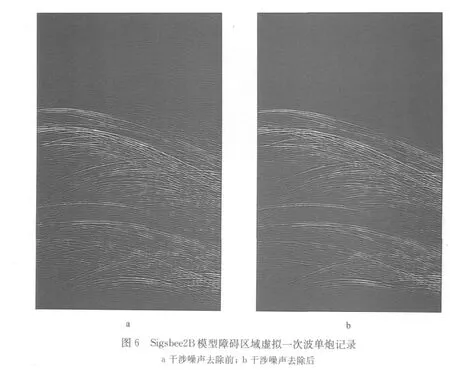
在此情况下，采用多次波成像补充地震一次波成像的方法技术，在炮震源缺失的区域利用已有炮数据构建虚拟一次波数据。图6a给出了构建的虚拟一次波数据的某单炮记录，可以看出，虚拟一次波中有效同相轴被覆盖了一层背景干涉噪声，用本文所述局部倾斜叠加方法对其进行去噪处理，结果如图6b所示。对比图6a和图6b可见，背景干涉噪声得到一定程度的压制。然后利用去噪后的虚拟一次波数据进行成像，得到的成像结果经过振幅和相位校正后补充到图5所示成像结果中，得到如图7所示的成像结果。可以看出，原先由于采集系统的间断导致缺失的地震一次波成像不足区域得到了弥补，从而得到了完善的地下构造成像信息。

图3 Sigsbee2B速度模型

图4 Sigsbee2B模型数据的某单炮记录

3.2 实际资料试处理

我们基于某探区的实际资料来测试本文方法的可行性和有效性。该区由于存在强波阻抗界面，极易产生多次波，不但有较强的全程多次波，局部测线段还存在层间多次波。

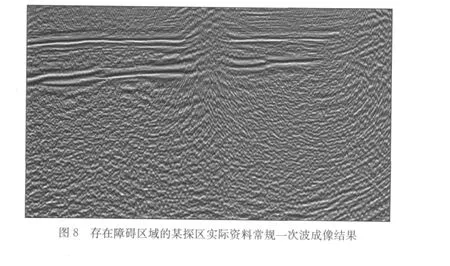
对该资料已有的炮数据只利用一次波进行偏移成像，得到如图8所示的成像结果。可以看出，由于炮数据缺失使得地下构造成像信息不完整。在此情况下，我们在没有炮点、只有检波点的区域，设置虚拟炮点和虚拟接收点，利用已有的炮数据构建缺失炮震源处的虚拟一次波数据。图9a是构建的虚拟一次波数据的某单炮记录。可以看出，虚拟一次波中有效同相轴被覆盖了一层背景干涉噪声。用本文所述局部倾斜叠加方法进行去噪处理，结果如图9b所示。对比图9a和图9b可见，背景干涉噪声得到一定程度的压制，有效波同相轴得到加强。利用去噪后的虚拟一次波数据进行成像，得到的成像结果经过振幅和相位校正后补充至图8所示的地震一次波成像结果中，得到如图10所示的成像剖面。由图10可见，原先由于采集系统中某些震源的缺失导致的常规一次波成像信息不足区域得到了补充，从而得到了完善的目标区域的地下结构信息。

图5 存在障碍区域的Sigsbee2B模型常规一次波成像结果

4 结束语

地震资料采集时若存在无法放炮、只能放置检波器的障碍区域，仅利用地震一次波进行成像会出现地下构造成像信息不足。若此区域地震多次波比较发育，那么可以通过利用地震数据中包含的多次波信息构建障碍区域的虚拟一次波，并通过虚拟一次波偏移成像结果来补充一次波成像信息的不足。与常规将多次波作为噪声进行压制的思路不同，本文方法充分挖掘、利用多次波中蕴含的信息来获取地下成像信息，弥补常规一次反射波成像的不足，从而和一次反射波一起为地下构造成像提供更加丰富和完整的信息。

［1］Foster D J，Mosher C C.Suppression of multiple reflections using the Radon transform［J］.Geophysics，1992，57（3）：386－395

［2］Lokshtanov D.Multiple suppression by data－consistent deconvolution［J］.The Leading Eage，1999，18（1）：115－119

［3］Lamont M G，Hartley B M，Uren N F.Multiple attenuation using the MMO and ISR preconditioning transforms［J］.The Leading Eage，1999，18（1）：110－114

［4］Berkhout A J，Verschuur D J.Estimation of multiple scattering by iterative inversion，Part I：theoretical considerations［J］.Geophysics，1997，62（5）：1586－1595

［5］Verschuur D J，Berkhout A J，Wapenaar C P A.Adaptive surface－related multiple elimination［J］.Geophysics，1992，57（9）：1166－1177

［6］Guitton A.Multiple attenuation with multidimensional prediction－error filter［J］.Expanded Abstracts of 73rdAnnual Internat SEG Mtg，2003，57－74

［7］Spitz S.Pattern recognition，spatial predictability，and subtraction of multiple events［J］.The Leading Edge，1999，18（1）：55－58

［8］Reiter E C，Toksoz M N，Keho T H，et al.Imaging with deep－water multiples［J］.Geophysics，1991，56（7）：1081－1086

［9］Guitton A.Shot－profile migration of multiple reflections［J］.Expanded Abstracts of 72ndAnnual Internat SEG Mtg，2002，1296－1299

［10］Muijs R，Robertsson J O A，Holliger K.Prestack depth migration of primary and surface－related multiple reflections：Part I—imaging［J］.Geophysics，2007，72（2）：S59－S69

［11］Remco M J，Robertsson J O A，Klaus H.Prestack depth migration of primary and surface－related multiple reflections：Part II—identification and removal of residual multiples［J］.Geophysics，2007，72（2）：S71－S76

［12］Liu Y K，Xu C.Reverse time migration of multiples［J］.Expanded Abstracts of 81stAnnual Internat SEG Mtg，2011，3326－3331

［13］Shan G.Source－receiver migration of multiple reflections［J］.Expanded Abstracts of 73rdAnnual Internat SEG Mtg，2003，1008－1011

［14］Shan G.Migration of surface－related multiples：tests on the Sigsbee2Bdataset［J］.Expanded Abstracts of 73rdAnnual Internat SEG Mtg，2004，1285－1288

［15］单国健.地表多次波应用研究［J］.石油物探，2007，46（6）：604－610 Shan G J.Application of surface－related multiples［J］.Geophysical Prospecting for Petroleum，2007，46（6）：604－610

［16］Sheng J.Migration multiples and primaries in CDP data by crosscorrelogram migration［J］.Expanded Abstracts of 71stAnnual Internat SEG Mtg，2001，1297－1300

［17］Yu J，Schuster G.Crosscorrelogram migration of IVSPWD data［J］.Expanded Abstracts of 71stAnnual Internat SEG Mtg，2001，456－459

［18］Curry W，Shan G.Interpolation of near offsets using multiples and prediction－error filters［J］.Expanded Abstracts of 78thAnnual Internat SEG Mtg，2008，2421－2424

［19］Wang Y，Luo Y，Schuster G T.Interferometric interpolation of missing seismic data［J］.Geophysics，2009，74（3）：SI37－SI45

［20］Berkhout A J，Verschuur D J.Full wavefield migration，utilizing surface and internal multiple scattering［J］.Expanded Abstracts of 74thAnnual Internat SEG Mtg，2011，3212－3216

［21］叶月明，李振春，仝兆岐，等.双复杂条件下带误差补偿的频率空间域有限差分法叠前深度偏移［J］.地球物理学进展，2008，23（1）：136－145 Ye Y M，Li Z C，Tong Z Q，et al.Prestack depth migration using F－X finite difference with error compensation in duplex complex conditions［J］.Progress in geophysics，2008，23（1）：136－145