基于物理光学假设的导体表面电流密度误差分析

姬金祖 马云鹏 黄沛霖 张中建

(北京航空航天大学 航空科学与工程学院，北京100191)

随着科学技术的发展，隐身技术越来越成为现代战争中的一项重要军事技术［1-3］.在隐身作战平台方案论证、概念设计阶段，往往通过数值计算得到目标的雷达散射截面(RCS，Radar Cross Section)，以便能够把握武器平台整体隐身性能［4-6］，因此快速预估大型目标 RCS非常重要.物理光学法(PO，Physical Optics)是一种重要的RCS快速预估方法［7-9］，其中关键的步骤就是通过PO假设得到金属散射体的表面电流密度.PO法计算表面电流密度基于无限大切平面假设，而且表面电流只存在照明面，阴影面的表面电流为0.根据物理光学假设，仅由入射方向、极化和表面法向就可以计算金属表面电流密度［10］.

本文对二维情形下基于PO假设的表面电流密度与精确解或矩量法(MoM，Method of Moments)的结果进行对比，研究不同散射体构型、入射波频率、极化的PO表面电流密度的误差.极化方面，考虑横磁波(TM，Transverse Magnetic)和横电波(TE，Transverse Electric)两种极化.TM波沿纵向只有电场分量，故电流沿着柱体母线，而TE波沿纵向只有磁场分量，故电流垂直于柱体母线.由PO表面电流计算公式，TM波表面电流随入射角发生变化，入射角越小，表面电流越大，垂直入射时表面电流最大.而由于TE波磁场强度H总沿着圆柱轴线方向，与表面法向垂直，故照明面表面电流幅度总为磁场强度的2倍［11］.此外，物理光学的表面电流与频率无关，而实际情况中表面电流的分布与频率有一定关系［12］.

本文采用导体圆柱、方柱和三角柱这3种构型研究PO法的表面电流密度误差.这3种构型分别代表了光滑外形、带有直角棱边的外形以及带有锐角棱边的外形.导体圆柱用精确解作为对比，导体方柱和三角柱没有精确解，用二维MoM计算结果进行对比.

1 导体圆柱表面电流

导体圆柱边界面与柱坐标系重合，可由分离变量法结合齐次边界条件计算得到金属圆柱表面电流密度分布的精确结果［10］.设圆柱半径为a，入射电磁波波数为k，电磁波从x轴正向入射，如图1所示.

图1 金属圆柱电磁波入射方向示意图

根据分离变量法和TM波、TE波满足的第一类及第二类齐次边界条件，可计算得到表面电流沿圆柱分布情况.为分析方便，假设入射平面电磁波H的幅度为1 A/m，计算得TM波和TE波表面电流密度［13］分别为

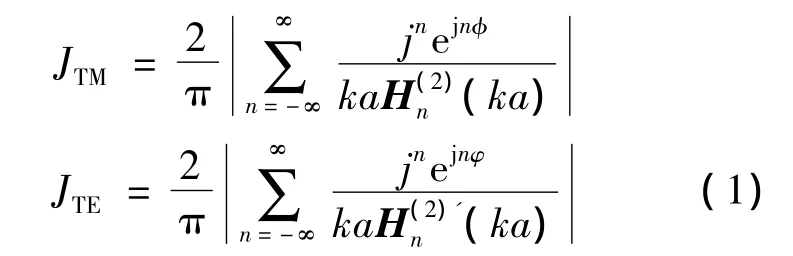
照明面PO表面电流密度计算公式［14］如下:

式中，Js表示表面电流密度;n表示表面法向;Hi表示入射磁场，PO表面电流密度不随ka变化.计算ka分别为10π，20π和40π时表面电流密度的精确解，并与PO表面电流进行对比.沿金属圆柱表面均匀选取360个采样点，用方位角φ表示，单位为(°).TM和TE表面电流密度计算结果对比如图2、图3所示.

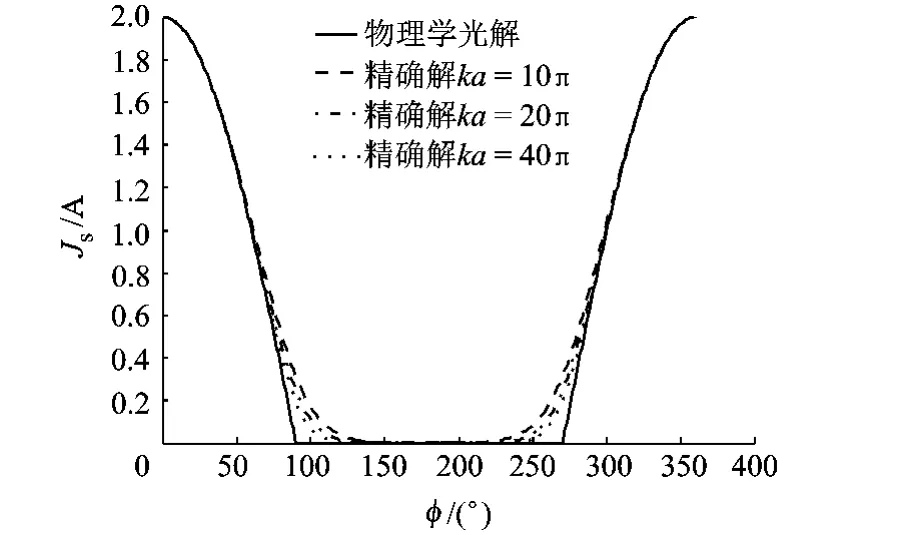
图2 TM波圆柱表面电流密度

图3 TE波圆柱表面电流密度

由图2、图3可见，TM情形PO表面电流密度与精确解比较一致，而TE情形PO表面电流的误差较大.两种极化下，ka越大，PO表面电流与精确解越接近，说明频率越高，物理光学近似越精确.

用360个采样点上PO表面电流与精确解之差的均方根来衡量误差大小，得到均方根误差随ka变化的曲线，如图4所示.

图4 PO法误差均方根随ka的变化

由图4可见，ka较小时，PO法表面电流误差很大.随着ka的增加，PO法表面电流计算结果误差逐渐减小.但是当ka较大时，误差随ka增大而减小的速度变得极其缓慢.比较极化的影响，TM波均方根误差比TE波小约一个数量级，可见PO表面电流密度在TM极化下精度更高.

2 金属方柱表面电流

2.1 正入射情形

金属方柱没有精确解，本文将PO法表面电流密度与MoM法计算结果进行对比.金属方柱边长为2 m，电磁波入射示意图如图5所示.

图5 金属方柱电磁波入射示意图

计算入射波长分别为0.5 m和0.2 m时的表面电流密度.MoM法计算中，线元长度设定为波长的1/10，则两种波长下未知元长度分别为0.05 m和0.02 m，将正方形的边分别划分成了160个和400个线元.右上角未知元的编号为1，编号沿逆时针方向增加.MoM法计算表面电流所用基函数为脉冲函数，采用点配法检验.

正入射情形，电磁波垂直照射到照明面，在照明面PO法表面电流密度为2 A/m，侧面和阴影面都为0.TM和TE情形下电流密度及与MoM法计算结果对比如图6所示，图中N表示表面电流元的编号.

由图6a可见，编号120～160的未知元是电磁波直接照射到的边，表面电流较大.TM波情形下，PO法表面电流密度较MoM略大，误差约为0.2 A/m.在电磁波直射的两个顶点，MoM表面电流密度出现突变，产生峰值，但PO法无法体现这种突变，这是由于TM情形表面电流沿着金属柱的纵向，故在棱边能够产生较强的电流.

a 波长0.5 m

图6 0°入射方柱表面电流密度对比

TE情形下，MoM表面电流呈现谐振特性，谐振周期与频率有关.由于电流沿金属柱周向，故电流在棱边传播受阻，不会产生像TM波一样的尖峰.金属方柱边长为4个波长，而照明面的谐振峰也恰好是4个.TE情形下的谐振峰在PO法假设中无法体现，这也形成了PO的误差来源.

在电磁波掠入射的边上(未知元编号1～40和80～120)，PO表面电流为0，但MoM表面电流非零，而且TM和TE还有较大的差别，TM波表面电流密度较小，约为0.2 A/m，而TE波表面电流密度则在1 A/m左右小幅振荡.比较而言，PO法计算TM波掠入射时的电流较准确，而计算TE波误差较大.在阴影面(未知元编号40～80)误差较小，PO法表面电流密度为0，MoM表面电流密度在两个极化下都与此接近，约为0.2 A/m.

比较图6a和图6b两种入射波长下表面电流的分布，基本特征相似，但有如下细微区别:①波长0.2 m较0.5 m的表面电流密度沿边长振荡较快，振荡幅度较低;②TM情形下，入射波长0.2 m的照明面和阴影面PO误差较入射波0.5m要大.

2.2 斜入射情形

下面研究入射电磁波沿45°方位角入射到金属方柱的情形，电磁波照射示意图如图5所示.

由于电磁波斜入射到两条边上，故TM和TE情形下的PO表面电流密度不同.入射波长0.5 m和0.2 m的表面电流密度分布如图7所示.

由图7a可见，编号1～40和120～160的未知元为照明面，其余的未知元为阴影面.TM情形的PO和MoM表面电流密度相差较小，表明TM极化下PO估算的表面电流密度误差较小.TE情形照明面MoM表面电流密度有较强振荡，但PO表面电流密度恒为2 A/m.阴影面TE极化MoM表面电流密度为0.5 A/m左右，但PO表面电流密度恒为0，这种情形下，TM极化PO表面电流密度较准确.

图7 45°入射方柱表面电流密度对比

由图7b可见，TM情形PO和MoM计算所得的表面电流密度基本一致.TE情形照明面MoM表面电流密度较入射波长0.5 m振荡更加剧烈，在阴影面产生了较大振荡，使PO表面电流密度估算误差更大.

综上所述，对金属方柱，TM波情形PO表面电流估算较为准确，而TE波情形PO表面电流估算误差较大.随入射波长见小，误差加大.

3 金属三角柱的表面电流

金属三角柱截面为等腰三角形，高为1 m，底边长为4 m.设入射波从右侧照射到左侧，如图8所示.

图8 金属三角柱电磁波入射方位示意图

设入射波长为0.5 m，将各边按波长的1/10划分为线元，共剖分成了167个未知量.用MoM法计算表面电流密度并与PO法结果进行对比.线元编号从左下角顶点开始，逆时针方向增加，如图8所示.PO和MoM表面电流密度对比如图9所示.

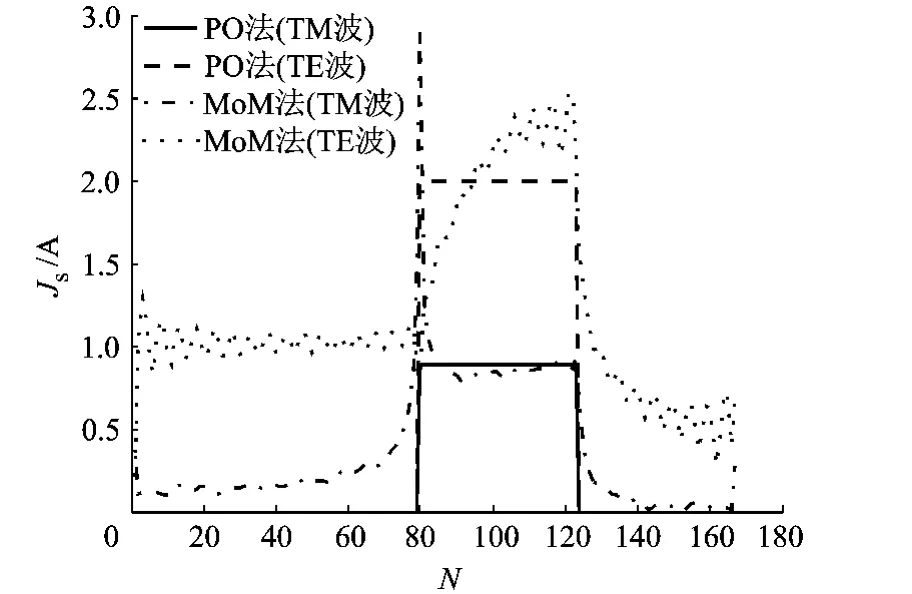
图9 0°入射三角柱表面电流密度对比

由图9可见，电磁波0°入射时，只有右侧一个面为照明面，对应线元编号为80～123.对TM波，PO和MoM表面电流密度基本一致，误差主要体现在底边以及顶点(未知元编号80).MoM法计算得到该顶点电流密度接近3 A/m，但PO法结果还不到1 A/m.在底边，电磁波呈掠入射状态，PO表面电流为0，MoM法表面电流密度约为0.25 A/m.

TE波PO表面电流密度为2 A/m，其余面为0.MoM计算结果说明照明面电流密度分布不均匀，基本变化趋势是从底边顶点到上边顶点电流密度逐渐变大，各顶点处也没有奇异性.在三角形底边(未知元编号1～80)，MoM表面电流密度在1 A/m上下谐振，这与电磁波掠入射到金属方柱侧面非常类似.左侧边上(未知元编号124～167)MoM表面电流密度约在0.5～1.0 A/m之间.

电磁波从30°方位角入射示意图如图8所示.表面电流计算结果对比如图10所示.

图10 30°入射三角柱表面电流密度对比

由图10可见，入射角30°时，三角形的两个腰都被照射到.TM波情形下，PO和MoM表面电流密度基本比较吻合，但在编号80的未知元处MoM表面电流产生一个尖峰，高达5A/m，这个尖峰在PO表面电流曲线中无法体现.TE情形，在右侧边上(未知元编号80～123)PO和MoM表面电流密度比较吻合，但在左侧边上，电磁波接近掠入射，PO表面电流为2 A/m，而MoM表面电流接近在1 A/m上下振荡.

4 结论

根据以上PO表面电流密度及其与精确解、MoM对比分析和讨论，有以下主要结论:

1)对于光滑表面，如金属圆柱，TM波表面电流计算结果较为准确，但在TE波情形下误差较大.PO表面电流分布的误差随频率增加而减少，但变化趋势随极化而不同，TM波比TE波的均方误差更大.

2)对于棱边的表面，如金属方柱和金属三角柱，TM波表面电流密度在棱边处误差较大，难以反映棱边的电流尖峰.在其他地方，PO法估算的表面电流密度比较准确.

3)TE波情形，电磁波掠入射时，表面电流密度恰好约等于入射磁场强度，有小幅振荡，而PO表面电流密度为0，而且也不能反映振荡特性.

4)总体而言，TE波PO表面电流密度误差较大，这是因为TE波照射到目标表面可以很容易形成爬行波，在散射体阴影面形成电流，而TM波的难以形成爬行波，阴影面电流较弱.

References)

［1］姬金祖，刘战合.基于面元分组的电磁遮挡算法及其优化［J］.北京航空航天大学学报，2009，35(4):453-456 Ji Jinzu，Liu Zhanhe.Electromagnetic occultation algorithm based on facets grouping and optimization ［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(4):453-456(in Chinese)

［2］ Mohajer M，Safavi-Naeini S，Chaudhuri S K.Surface current source reconstruction for given radiated electromagnetic fields［J］.IEEE Transactions on Antennas and Propagation，2010，58(2):432-439

［3］何国瑜，卢才成，洪家才，等.电磁散射的计算和测量［M］.北京:北京航空航天大学出版社，2006:196-204 He Guoyu，Lu Caicheng，Hong Jiacai，et al.Calculation and measurement of electromagnetic scattering［M］.Beijing:Beihang University Press，2006:196-204(in Chinese)

［4］关莹，龚书喜，徐云学，等.适用于裁剪NURBS曲面RCS预估的改进的物理光学法［J］.西安电子科技大学学报，2010，37(5):893-898 Guan Ying，Gong Shuxi，Xu Yunxue，et al.Improved PO technique for the RCS computation of targets modeled with trimmed NURBS surfaces ［J］.Journal of Xidian University，2010，37(5):893-898(in Chinese)

［5］陈博韬，雷振亚，谢拥军，等.基于改进物理光学法的电大目标双站 RCS的预估［J］.电波科学学报，2010，25(5):960-965 Chen Botao，Lei Zhenya，Xie Yongjun，et al.Bistatic RCS prediction with improved PO method for electrically large targets［J］.Chinese Journal of Radio Science，2010，25(5):960-965(in Chinese)

［6］关莹，龚书喜，张帅，等.时域物理光学法分析均匀介质目标的瞬态散射［J］.电波科学学报，2011，26(3):515-520 Guan Ying，Gong Shuxi，Zhang Shuai，et al.Transient scattering analysis of electrically large homogeneous dielectric targets by using TDPO method ［J］.Chinese Journal of Radio Science，2011，26(3):515-520(in Chinese)

［7］ Li Jianbing，Wang Xuesong，Qu Longhai.Calculation of physical optics integrals over NURBS surface using a delaminating quadrature method［J］.IEEE Transactions on Antennas and Propagation，2012，60(5):2388-2397

［8］ Jackson J A.Analytic physical optics solution for bistatic 3D scattering from a dihedral corner reflector［J］.IEEE Transactions on Antennas and Propagation，2012，60(3):1486-1495

［9］ Letrou C，Boag A.Generalized multilevel physical optics(MLPO)for comprehensive analysis of reflector antennas［J］.IEEE Transactions on Antennas and Propagation，2012，60(2):1182-1186

［10］ Liu Ziliang，Wang Chaofu.Efficient iterative method of moments physical optics hybrid technique for electrically large objects［J］.IEEE Transactions on Antennas and Propagation，2012，60(7):3520-3525

［11］ Zhang Jun，Yu Wenming，Zhou Xiaoyang，et al.Efficient evaluation of the physical optics integrals for conducting surfaces using the uniform stationary phase method［J］.IEEE Transactions on Antennas and Propagation，2012，60(5):2398-2408

［12］ Huang K，He Z L，Zhang H W，et al.Efficient analysis of antenna around electrically large platform with improved non-uniform rational b-spline hybrid method of moments and physical-optics method［J］.IET Microwaves Antennas and Propagation，2011，5(2):136-141

［13］ Tasic M S，Kolundzija B M.Efficient analysis of large scatterers by physical optics driven method of moments［J］.IEEE Transactions on Antennas and Propagation，2011，59(8):2905-2915

［14］ Umul Y Z.Physical optics scattering of waves by a half-plane with different face impedances［J］.IEEE Antennas and Wireless Propagation Letters，2011，10:21-24