吸气式高超声速飞行器推进系统耦合建模与分析

唐硕, 张栋, 祝强军

(1.西北工业大学 航天学院, 陕西 西安 710072;2.西北工业大学 航天飞行动力学重点实验室, 陕西 西安 710072)

2012-08-25;

2012-12-24; < class="emphasis_bold">网络出版时间

时间:2013-04-09 09:58

西北工业大学博士论文创新基金资助(CX201218)

唐硕(1963-)，男，四川达州人，教授，博士生导师，研究方向为飞行器动力学与控制、飞行仿真；

张栋(1986-)，男，宁夏青铜峡人，博士研究生，研究方向为高超声速飞行器动力学建模。

吸气式高超声速飞行器推进系统耦合建模与分析

唐硕1, 张栋1, 祝强军2

(1.西北工业大学 航天学院, 陕西 西安 710072;2.西北工业大学 航天飞行动力学重点实验室, 陕西 西安 710072)

吸气式高超声速飞行器机体/推进一体化设计,使得外形-气动-推进强耦合,给飞行器建模与控制带来巨大挑战。建立了一种基于准一维流动理论结合激波膨胀波方法的推进系统耦合分析模型,得到影响推进系统性能的因素,包括几何外形、迎角、马赫数、飞行高度、当量比等,以真实反映系统耦合特性。通过仿真计算分析了这些因素对推进系统性能的影响规律,可为飞行器初步设计阶段方案论证及一体化优化等问题提供基础和理论依据。

推进系统; 激波膨胀波; 耦合模型; 一体化设计

0 引言

高超声速飞行器是指以吸气式及其组合发动机为动力,在大气层内或跨大气层以马赫数5以上的速度远程巡航飞行的飞行器[1]。与常规飞行器相比,其机体/推进一体化设计,给气动、推进建模及其控制器设计带来巨大挑战[2]。

吸气式高超声速飞行器最显著的特点是学科之间强耦合。文献[3]通过设计结构矩阵,清晰地表示一体化设计框架中各学科之间的耦合关系。其中以机体与超燃冲压发动机之间的耦合最为突出,前体下表面作为超燃冲压发动机外压缩段,对来流进行减速增压,后体下表面作为超燃冲压发动机外喷管起到继续膨胀燃气的作用。文献[4]指出飞行器气动特性影响推进性能,进气道对空气的压缩效率、燃料能力的释放以及剪切层位置和形状都受到俯仰角速度和动压的影响。Schmidt等[5]指出燃料流量和进气道扩散面积比可以改变飞行器的俯仰角速度。文献[6]中基于大量气动插值数据,对机体/推进一体化耦合特性进行分析研究。

吸气式高超声速飞行器机体/推进一体化设计,需要考虑机体和推进系统相互影响,在进行高超声速飞行器建模时,就应该充分考虑这种耦合特性。基于此,本文建立了推进系统的耦合分析模型,分析了几何外形、气动特性等因素对推进系统性能的影响。

1 吸气式高超声速飞行器模型

本文采用文献[7]中的高超声速飞行器模型,高超声速飞行器机体/发动机一体化设计,超燃冲压发动机置于高升阻比的机体下腹部,使得飞行器的前体下壁面和后体下壁面既是飞行器的气动界面,又分别是超燃冲压发动机进气道的外压缩段和发动机尾喷管的外膨胀段。这样的一体化构型,使得不能准确地划分气动和推进界面,不同的划分气动、推进界面的方法计算得到的气动和推进系统性能指标的数值及物理意义相差很大。为了建立高超声速飞行器推进系统耦合分析模型,研究外形、气动参数对推进系统的影响,本文采用如图1所示的算力体系,将整个前体下壁面及其发动机内流道划分为推进系统,外喷管型面受力计算划分为气动学科。

图1 算力体系的划分Fig.1 Calculation force system division

2 推进系统耦合建模

根据本文所建立的算力体系,图2给出了典型的吸气式高超声速飞行器推进系统二维简图,可以看出,吸气式高超声速飞行器推进系统由前体下表面、扩压段、隔离段、燃烧室和内喷管组成。

图2 高超声速飞行器推进系统二维平面示意简图Fig.2 Two-dimensional plane diagram of hypersonic vehicle propulsion system

表1给出了超燃冲压发动机简图中相关参数的定义。

表1 推进系统参数说明Table 1 Propulsion system parameter description

2.1 前体下表面气流参数计算

高超声速飞行器前体下壁面作为推进系统的压缩段,主要作用是通过对来流的压缩给进气道提供均匀气流,根据一维斜激波公式求得进气道入口参数[7]。

(1)

式中,δi为前体压缩角;Ma∞,T∞,P∞分别为来流马赫数、静温和静压;γ为比热比。

2.2 扩压段

扩压段的入口参数为前体进行多级压缩后的均匀气流,其出口参数又作为隔离段入口参数,气流通过扩压段的参数变化关系为[8]:

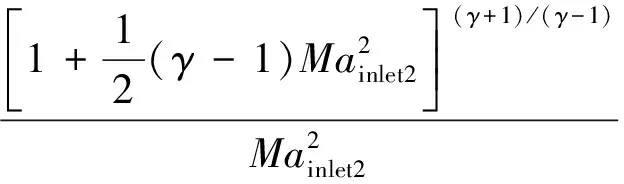
(2)

(3)

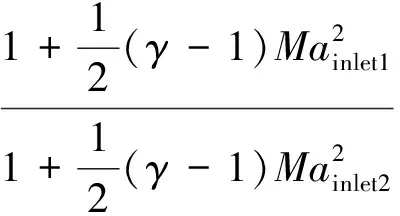
(4)

通过式(2)～式(4)求得隔离段入口气流马赫数Mainlet2、静压Pinlet2及其静温Tinlet2:

(5)

2.3 隔离段建模分析

隔离段是在飞行器前体/进气道和燃烧室之间设置的一定长度的等截面通道,是进气道和燃烧室之间的气动力/热缓冲段,同时还可以对来流气体进一步压缩。当燃烧室由于燃烧放热引起压力剧烈升高时,在燃烧室的反压作用下,隔离段会产生激波串,激波串的位置和长度随上下游的压力比和马赫数而变化,在一定的压力范围内,隔离段能够很好地起到保护隔离作用,使进气道流场不会受到燃烧室压力升高而造成的影响。

忽略摩擦和热传递的情况下,设隔离段出入口静压比为Pr=Piso/Pinlet2,则隔离段出口马赫数为[9]:

Maiso=

(6)

隔离段的出口温度为[10]:

(7)

根据隔离段激波串前后最大压力比小于一道正激波的压力比,则隔离段中激波串强度极限为一道正激波[11],有:

(8)

通过式(6)～式(8)求得燃烧室入口气流马赫数Maiso、静压Piso及其静温Tiso:

(9)

2.4 燃烧室建模

燃烧室的流动为一维瑞利流动,气流通过燃烧室后的参数变化关系为[8]:

(10)

(11)

(12)

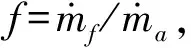
用燃油当量比作为推进系统的一个控制量比ΔTc作为控制量更便于计算和归一化处理。燃油当量比(Φ=f/fst),即为油气比的无量纲化其中fst为化学当量油气比。

根据燃烧室的能量守恒方程有[12]:

(13)

式中,ηc为燃烧效率;Hf为燃料的热值。因此可以得到燃烧室出口静温与入口静温之比:

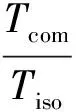
(14)

通过式(14)可以求出ΔTc:

ΔTc=Tcom-Tiso

(15)

把式(15)带入式(10)计算可得燃烧室出口气流马赫数Maiso、静压Piso及其静温Tiso:

(16)

2.5 内喷管建模

内喷管出口气流参数与入口气流参数的关系为[8]:

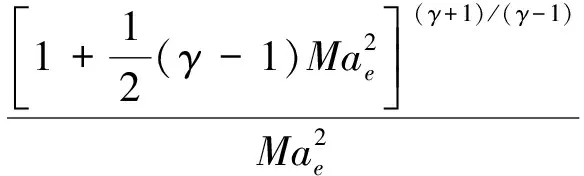
(17)

(18)

(19)

通过式(17)～式(19)可求得内喷管出口气流马赫数Mae、静压Pe及其静温Te:

(20)

2.6 推力的计算

根据本文划分的算力体系结合动量定义可以求得单位宽度发动机推力为:

(P1-P∞)A1

(21)

(Pe-P∞)Ae-(P1-P∞)A1

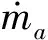
(22)

3 仿真计算与耦合影响分析

推力FT和推力系数CT是超燃冲压发动机重要的性能指标之一,因此本文选CT作为推进系统的性能指标研究了外形-气动等因素对推进系统的影响。以某吸气式高超声速飞行器外形为研究对象,设计工况为:飞行高度H=25 km;来流马赫数Ma∞=6;迎角α=0°。前体压缩角优化后的初始值为[3.547°,1.872°, 2.985°,4.523°];隔离段静压比设计值Pr=10;当量比设计值Φ=0.65;燃料为H2;fst=0.029 1;Hf=119 954 kJ/kg。

3.1 形改变对推进系统性能影响分析

对来流空气的外压缩由前体下壁面楔形体组织的激波系完成,内压缩由外罩内壁组织的激波系完成,因此前体楔形角变化影响推进系统性能。图3为前体第一级压缩角对推进系统性能的影响规律,可以看到随着压缩角的增大,推力系数增大。当第一级压缩角大于5°,而其他条件不变的情况下,燃烧室会发生热雍塞,发动机不能够正常工作,可见前体压缩角的优化配置对推进系统性能的影响非常关键。

图3 前体压缩角对推进系统性能影响规律Fig.3 Influence of precursor compressed angle influence on the propulsion system performance

3.2 迎角对推进系统性能影响分析

对于吸气式高超声速飞行器,迎角变化对飞行器性能有强烈影响,因此迎角一般只在较小范围内进行调节。图4是不同来流迎角下推进系统性能参数,计算中迎角变化范围为-2°～4°。当迎角从-2°变化到2°时,推力系数增幅较大;当迎角大于2°时,推力系数增幅较小;当迎角大于4°时,燃烧室发生热雍塞,发动机工作不正常,这时需要降低当量比,推力系数逐渐减小。

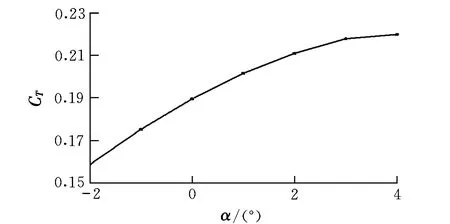
图4 迎角对推进系统性能影响规律Fig.4 Influence of angle of attack influence on thepropulsion system performance

3.3 发动机控制参数对推进系统性能影响分析

文献[8,13]把当量比、扩压段面积比及内喷管面积比作为超燃冲压发动机的控制量,基于此,本文分析了这些量对推进系统性能的影响,同时考虑了隔离段静压比对推进系统性能的影响,仿真结果如图5～图8所示。

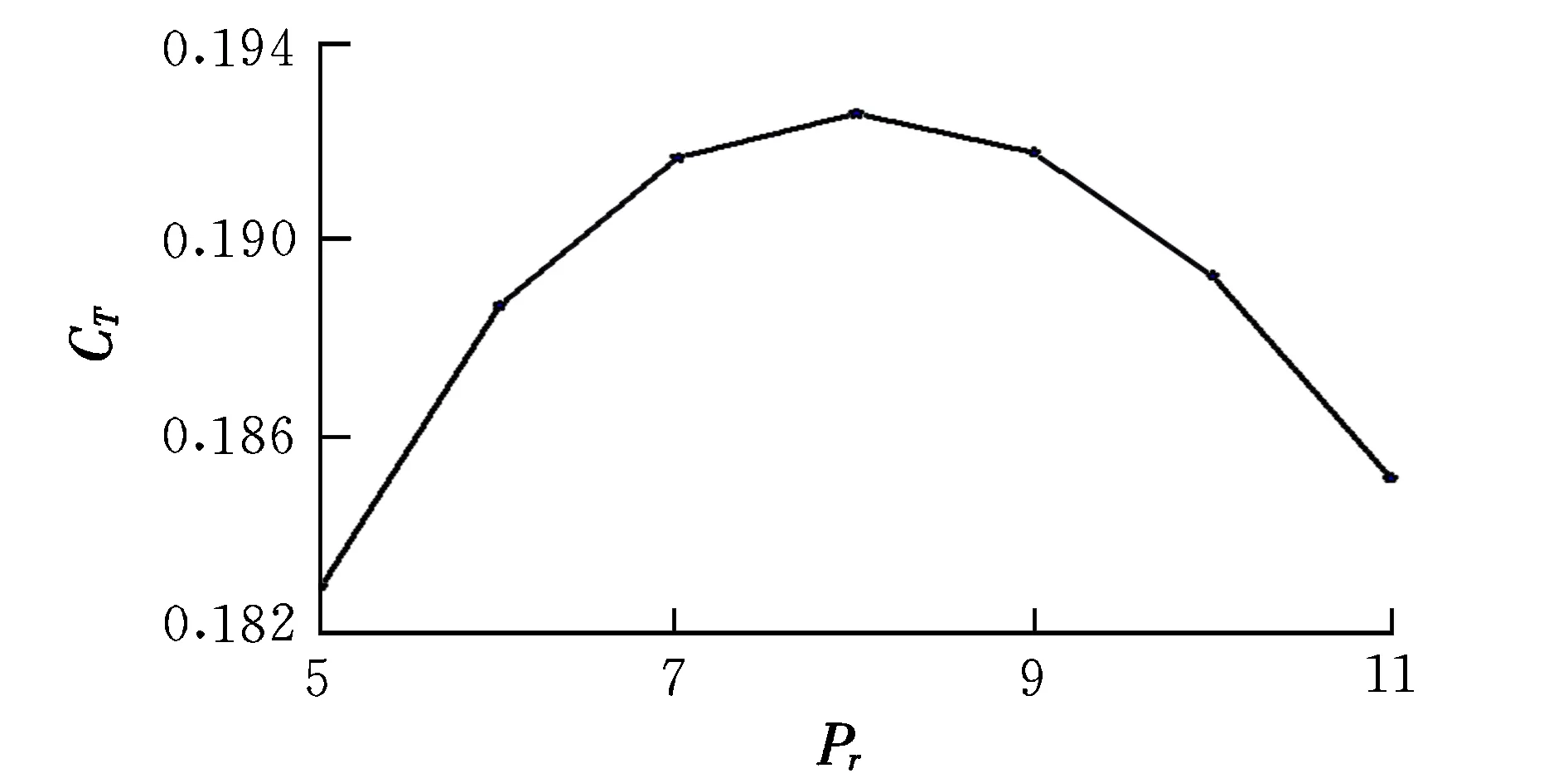
图5 隔离段静压比对推进系统性能影响规律Fig.5 Influence of isolator static pressure ratio influence on the propulsion system performance

从图5可以看到,随着隔离段静压比的增大,推力系数先增大,后减少,静压比增大意味着燃烧室入口气流的压强会增大,过高的燃烧室入口压强导致燃料和空气反应的断链,影响推进系统性能。

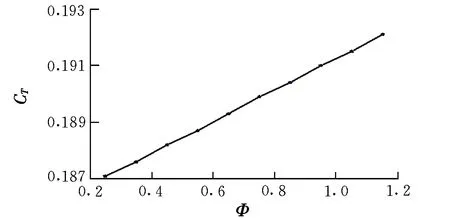
图6 燃油当量比对推进系统性能影响规律Fig.6 Influence of fuel equivalence ratio influence on thepropulsion system performance

从图6可以看到,随着当量比的增加,推力系数不断增大,但增幅很小,当量比每增加0.1,推力系数增加不到0.001;当量比大于1时,推力系数仍有明显增大,这说明燃料没有完全燃烧,否则在富油状态下,推力系数不会继续增加。

图7～图8分别为内喷管面积比、扩压段面积比对推进系统性能的影响规律。可以看到,随着内喷管面积比的增加,推力系数不断减小,而且幅度较大,内喷管面积比每增加0.1,推力系数减小幅度大于0.011。随着内喷管面积比的增大,膨胀不够充分,内喷管出口马赫数增大,出口静压减小,从而导致推力系数减小。随着扩压段面积比的增大,推力系数减少,而且幅度较大,扩压段面积比每增加0.1,推力系数减小的幅度大于0.015。随着扩压段面积比的增大,压缩性能下降,扩压段出口马赫数增大,静压减小,没有达到高效压缩的效果,导致推力系数减小。

图7 内喷管面积比对推进系统性能影响规律Fig.7 Influence of nozzle area ratio influence on the propulsion system performance

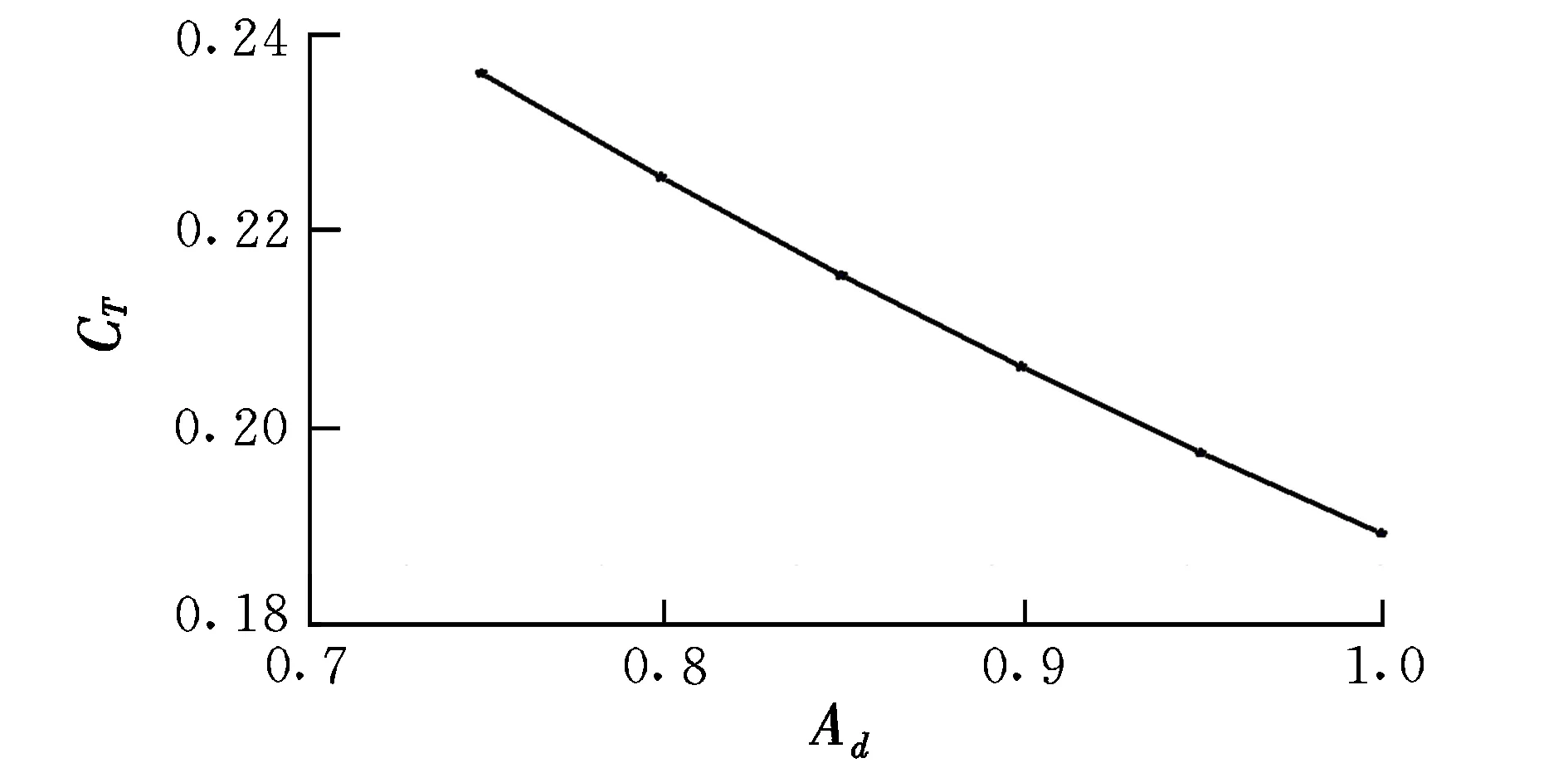
图8 扩压段面积比对推进系统性能影响规律Fig.8 Influence of diffuser area ratio influence on the propulsion system performance

4 结论

吸气式高超声速飞行器机体/推进一体化设计使得外形-气动-推进强耦合。本文通过准一维流场分析，结合激波膨胀波理论对此类飞行器的推进系统进行耦合建模与仿真计算，得到以下结论:

(1)外形-推进系统强耦合。压缩角变化对推进系统性能影响很大,前体压缩角每增加0.5°,推力系数增幅超过0.01,当第一级前体压缩角超过额定值时(本文研究中为5°),燃烧室出现热雍塞,发动机不能正常工作。因此对此类飞行器进行设计时,要结合推进系统性能要求、气动性能要求对前体压缩角进行设计和优化,而且要进行迭代设计,在保证发动机高效工作的前提下,使前体压缩性能最高。

(2)迎角对推进系统性能有强烈影响。当迎角在-2°～2°时,迎角每增加1°,推力系数增幅超过0.01；当迎角大于2°时,迎角每增加1°,推力系数增幅约0.005,变化幅度较小；当迎角大于某额定值(本文研究中为4°),燃烧室出现热雍塞,发动机不能正常工作。

(3)扩压段面积比、内喷管面积比对推进系统影响剧烈,因此在进行飞行器设计时,需要考虑内喷管的扩张比及其进气道收缩比,这些参数需要在一个合理的范围内变化,可以使得飞行器整体性能最优。

吸气式高超声速飞行器推进系统的建模与分析非常复杂,涉及到隔离段内的激波干扰、边界层影响,燃烧室内的燃料喷射方式、壁面摩擦、传热、粘性干扰等因素。本文的研究旨在建立包含外形、气动的推进系统耦合模型,探索外形、气动及发动机参数对推进系统的影响规律,对于飞行器的前期设计阶段具有重要的理论指导意义。

[1] 王振国,梁剑寒,丁猛,等.高超声速飞行器动力系统研究进展[J].力学进展, 2009,39(6):716-739.

[2] Richman M S,Kenyou J A,Sega R M.High speed and hypersonic science and technology[R].AIAA-2005-4099,2005.

[3] 罗世彬.高超声速飞行器机体/发动机一体化及总体多学科设计优化方法研究[D].长沙:国防科学技术大学,2004.

[4] Fidan B C S,Mirmiraniz M,Logannou P A.Flight dynamic and control of air-breathing hypersonic vehicles:review and new directions[C]//12th AIAA International Space Planes and Hypersonic Systems and Technologies.Norfolk,Virginia,2003:1-24.

[5] Schmidt D K,Mamich H,Chavez F.Dynamics and control of hypersonic vehicles, the integration challenge for the 1990s[C]//AIAA Third International Aerospace Planes Conference.Orlando,FL,1991:1-11.

[6] Clark A,Wu C,Mirmirani M.Development of an airframe propulsion integrated generic hypersonic vehicle model[R].AIAA-2006-218,2006.

[7] 车竞.高超声速飞行器乘波布局优化设计研究[D].西安:西北工业大学,2006.

[8] Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle [J].Journal of Spacecraft and Rockets,2007,44(2):374-387.

[9] Heiser W H,David T P.Hypersonic airbreathing propulsion [M].AIAA Education Serises,Published by American Institute of Aeronautics and Astronautics,1994.

[10] 刘陵.超音速燃烧与超音速燃烧冲压发动机[M].西安:西北工业大学出版社,1993:258-446.

[11] 蔡国飙,徐大军.高超声速飞行器技术[M].北京:科学出版社,2012:72-77.

[12] Ikawa H.Rapid methodogy for design and performance prediction of integrated supersonic combustion ramjet engine[J].Journal of Propulsion and Power,1991,7(3):437-444.

[13] Chavez F R,Schmidt D K.Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis [J].Journal of Guidance,Control,and Dynamics,1994,17(6):1308-1319.

Couplingmodelandanalysisforair-breathinghypersonicvehiclepropulsionsystem

TANG Shuo1, ZHANG Dong1, ZHU Qiang-jun2

(1.College of Astronautics, NWPU, Xi’an 710072, China;2.National Key Laboratory of Aerospace Flight Dynamics, NWPU, Xi’an 710072, China)

The integrated design of air-breathing hypersonic vehicle airframe and propulsion system, which brings strong coupling between configuration, aerodynamics and propulsion, makes modeling and control of hypersonic vehicles an extreme challenge. A propulsion analysis model based on the theory of quasi-one-dimensional flow and shock-expansion wave is presented in this paper, and the influence factors on the performance of propulsion system are obtained, including geometric parameters, aerodynamics, flight height and equivalence ratio, etc. The model reflects the characteristic of system coupling. The effects of these factors are determined via computer simulation. The conclusions in this paper can be served as the basis for AHV design optimization in the preliminary design stage.

propulsion system; shock expansion; coupling modeling; integration configuration

V211.5

A

1002-0853(2013)03-0244-06

(编辑：李怡)