基于多媒体学习理论的大学数学教学设计

庞 坤

（中国人民武装警察部队学院 基础部 数学教研室，河北 廊坊 065000）

1 引 言

随着信息技术的快速发展，目前大学数学教学普及了多媒体教学，多媒体能够呈现多样、动态、丰富的信息，具有传统教学工具所不具备的许多优势，它较好地解决了大学数学授课内容多而学时少等教学矛盾，改变了传统的单调教学模式，促进了课堂教学内容、教学方法、教学过程的全面优化，提高了教学效果[1～2].于是人们普遍认为，多媒体教学能够引起学习者的兴趣；能够适应不同学习者的需要与偏好，从而可大大提高其投入程度，实现良好的学习效果.但是，长期以来对于多媒体教学效果的研究表明，真实的情况并非如此简单、乐观.认知心理学的研究表明，通过任何媒体形式获取的信息必然要受到人类信息加工系统的影响.工作记忆是指为完成某一任务而实时保持信息，并对保存的信息进行操作加工的系统.研究发现，人类信息加工容量很小，只能存储7个左右的信息单元，而如果要加工信息，则一次只能处理2～3个组块的信息.信息系统对于信息的保持时间极短[3].信息加工系统作为信息存储和加工的主要场所，如何有效地利用其资源必然成为大学数学教学设计时需要考虑的一个重要问题.在多媒体教学设计中，有可能会造成学生认知超载，最终对学习效果产生负面影响.以下将基于多媒体学习理论，分析探讨目前大学数学多媒体教学中认知超载的类型，并加以解决.

2 多媒体学习理论

心理学家Mayer提出生成性多媒体学习理论[4].Mayer认为，人有听觉和视觉两个通道，通过听觉通道选择相关文字形成命题表征，组成言语模型，通过视觉通道选择重要图像形成图像表征，组成图片模型，听觉和视觉两个通道的认知加工建构了两种平行的心理模式.如果这两种心理模式同时呈现在工作记忆中，就会发生整合加工（如图1）.

图1中附有文字标识的箭头表示认知加工.譬如，“整合”的箭头表示言语、图片模型及相关的先前知识被融合.在多媒体学习中，5种认知加工，即选择文字、选择图片、组织文字、组织图片和整合都是主动加工.这些加工强调信息加工系统的认知容量.

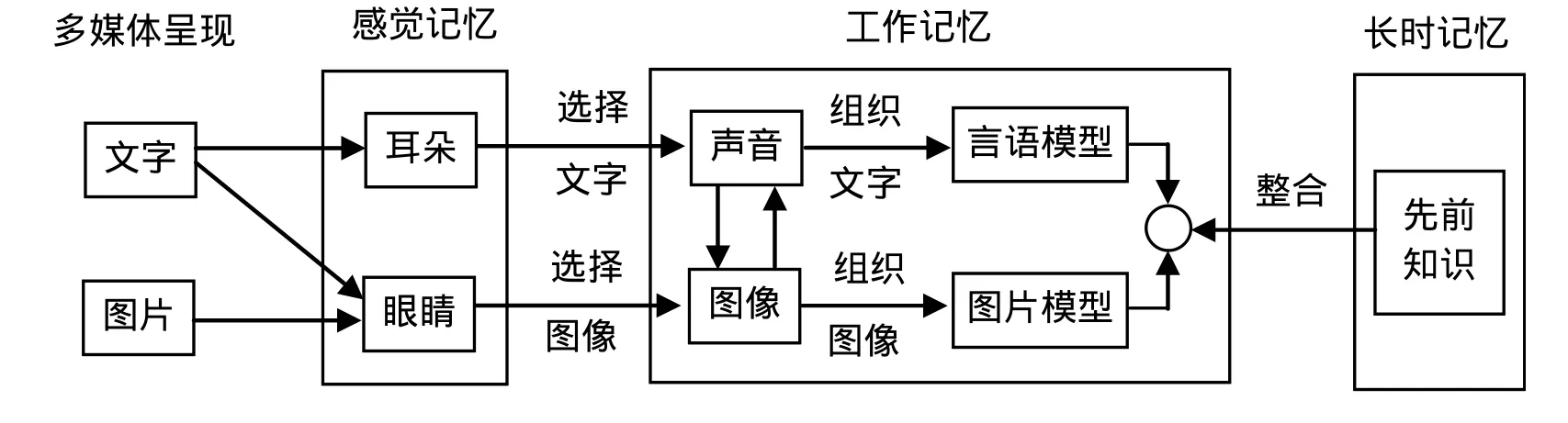
图1 多媒体学习中的认知理论

3 大学数学教学认知超载类型

认知需求分为必要加工、不必要加工和表征保持[5].必要加工是指弄清呈现材料意义的认知加工.不必要加工是指在对于理解材料的意义上不需要，但在设计学习任务时又被预先准备了的认知加工.表征保持是指在工作记忆中认知加工需保持心理表征一段时间.总加工是必要加工、不必要加工和表征保持的总和.当学生需要的认知加工容量超过其具有的认知容量时，会出现认知负荷超载，简称认知超载.重新分配必要加工、减少不必要加工，或者减少表征保持可减少认知负荷.

3.1 一个通道被必要加工的认知需求超载

如果教学中教师在屏幕上只呈现和讲解文本，而学生在很大程度上难理解文本意义.这可能是因为文本在听觉通道被加工的认知需求超载，解决对策是呈现文本和与文本相应的图片，在听觉通道和视觉通道中文本被加工，在视觉通道中图片被加工，听觉通道的认知需求超载就卸载到了视觉通道.大学数学教学内容复杂、抽象，很多内容若没有相应的图形呈现，学生理解非常困难.如计算曲面面积的公式，如果没有相应的图形呈现，学生无法理解柱面、曲面和切平面的关系，更无法理解切平面上的小片平面的面积可以近似代替相应小片曲面的面积；又如理解球面坐标中的体积元素，若不呈现空间坐标，学生不易理解直角坐标与球面坐标的关系，从而不能理解球面坐标各微小增量所成的六面体的体积即体积元素可近似看成长方体的体积.再如拉格朗日中值定理的证明，曲线、曲面积分等，如果没有图像呈现，教学几乎无法进行.

如果教学中教师在屏幕上同时呈现动画和描述动画形成的文本，那么当学生看动画时，就不能阅读文本，学生阅读文本时，就不能看到动画.解决对策是以教师的讲解代替呈现文本.在听觉通道中言语被加工，在视觉通道中只有动画被加工.所以，视觉通道的认知需求超载就卸载到了听觉通道，对视觉通道的认知加工要求被减少了，学生能够更好地选择动画的重要部分进行进一步加工.同时因为听觉通道的认知加工要求也是有限的，所以，教师必须精讲，学生再选择教师精解中的重要部分进行进一步加工.如极限概念的引入，教师在屏幕上呈现描述割圆术中圆内接正多边形正6´2n-1多边形面积通过边数的不断增加逼近该圆面积的无限变化的过程动画的同时，教师口头讲解“……割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣……”，而不必把刘徽的这段话呈现在屏幕上.又如大学数学教学中涉及许多复杂的曲面立体，教师在讲解并呈现曲面立体动画形成时，可不再呈现动画形成的文本.

3.2 两个通道被必要加工的认知需求超载

如果教学中教师在屏幕上呈现动画的同时，讲解动画的形成，而动画呈现的频率较快且动画形成的内容很丰富，此时，当学生从呈现的学习材料中选择相关的言语和图片时，下段学习材料又开始呈现了，学生没有足够的时间对选择的相关言语和图片进行深层次的加工.听觉通道和视觉通道都被必要加工的认知需求超载.解决对策是建议分割学习材料或使学生接受预先训练.

分割学习材料是呈现的材料被分成几个小片段，教师在屏幕上呈现片段之间给学生留一些时间思考，从而学生能够从这些片段中选择重要的言语和相关的图片，进行组织和整合.如从几何与力学问题出发引进定积分的定义，求曲边梯形的面积和变速直线运动的路程，采取以分割、近似、求和、取极限为关键词的4个片段，每个片段的呈现都留给学生足够多的时间对关键词进行深层次的加工，组织和整合4个片段的关键信息，使学生最终能抛开几何与力学问题的具体意义，抓住它们在数量关系上共同的本质与特性加以概括，从而抽象出定积分的定义.

预先训练是让学生预先接受即将进行的学习系统中某些重要部分的提前指导.建构心理模型需要两步：成分模型的建构和因果模型的建构.成分模型的建构涉及学习系统中重要成分如何工作，因果模型的建构涉及学习系统中一个部分的改变如何造成系统中另一个部分的改变.如在间断点的分类中，学生必须同时建构成分模型和因果模型，通过预先训练成分，学生熟练掌握极限和连续概念，学生可以更有效地加工教师对于屏幕上各种图形间断点类型的讲解，即学生把他的认知容量用到建构因果模型上.如果学生没能预先熟练掌握极限和连续概念，学生就很难理解并掌握极限、连续和间断点之间的因果联系，在这种情境下，让学生理解、判断间断点类型，此任务很容易使工作记忆超载.

3.3 无关材料被不必要加工需求超载

基于多媒体学习理论，在教学中教师加入有趣、但与配有讲解的动画无关的材料时，有可能造成学生把有限的认知资源使用到不必要加工上.在大学数学教学中，概念或公式原理形成的步骤都是必要加工，背景音乐是不必要加工.教师讲解屏幕上的概念或公式原理形成的步骤时，如果同时伴随着背景音乐不必要加工，学生有可能对概念、公式或定理不能进行有意义学习的认知加工，学生的认知负荷被背景音乐的不必要加工需求超载.因此，在大学数学教学中，删除如背景音乐这些有趣但与教学内容无关的材料，可使得教师的讲解过程尽可能的简洁和有条理，学生将只进行与教学内容相关的材料的必要加工.

3.4 必要材料被不必要加工需求超载

当由必要材料呈现方式而引起不必要加工，造成系统超载，无关材料被不必要加工需求超载和必要材料被不必要加工需求超载是不同的：学习任务要求虽都是不必要加工，但造成认知负荷超载的原因不同.无关材料被不必要加工需求超载中强调的是呈现无关的材料，必要材料被不必要加工需求超载中强调的是必要的材料以杂乱排列的方式呈现.解决对策是进行有序排列或消除冗余.

进行有序排列是指合适放置文字和图形.当文本和相应的图片距离较远时，学生要用有限的认知资源扫描图形，以便于找到图形中对应的部分，就会产生必要材料被不必要加工需求超载.如在图形之中，把相应文字放置在靠近它所描述的成分时，可以减小不必要加工造成的认知负荷.在大学数学教学中，有大量的复杂图形呈现，如多维曲线、曲面等，在进行教学设计时，要合理安排图形和相应说明文字的位置.

在多媒体教学中，教师讲解、呈现动画和文本，当教师讲解的内容在屏幕上又以文本的方式同时呈现时，学生必须安排认知容量去加工讲解和文本这两种形式呈现的同一内容.研究发现：以一种形式呈现比同时用两种形式呈现同一内容的学习效果好[6].这时建议消除冗余.“消除冗余”与“删除”相似，因为两种方法都涉及去掉多媒体呈现中的一部分，但它们存在差异：“删除”涉及去掉有趣的但无关的材料，但“消除冗余”是去掉必要材料的不必要的复本.事实上，消除冗余与一个通道被必要加工的认知需求超载的类型是相符合的.

3.5 一个或两个通道被必要加工和表征保持联合超载

在教学中，如果教师首先对描述概念或公式原理形成的步骤进行讲解，然后再在屏幕上呈现描述概念或公式原理形成的动画步骤，那么按照多媒体学习理论，这种先讲解再呈现对应动画的形式可能会增加学生的认知负荷.因为当对应的动画呈现时，学生必须在其工作记忆中拥有先前讲解的言语表征，这样，学生必须拿出工作记忆中的一部分认知容量用于保持概念或公式原理形成的言语表征，这样就不得不消耗了学生用于选择、组织和整合的认知加工容量，造成必要加工和表征保持的联合超载.解决对策是使对应的听觉和视觉材料同步呈现.“时间接近效应”[7]的研究表明：当对应的听觉和视觉材料同步时，不必等到视觉材料出现时还要在工作记忆中保持听觉材料的表征，这能使认知负荷达到最小化.当连续呈现的材料被分割成小块时，如果交替呈现几秒钟的讲解和几秒钟的动画，不会出现“时间接近效应”，因为在工作记忆中只有少量听觉或视觉材料需要表征保持，学生工作记忆不会产生认知超载.大学数学的教学内容具有高度的抽象性，无论概念、公式还是习题，步骤都有很强的逻辑性，如果教师先把其解题思路及解法叙述完，再在屏幕上一次性呈现解法过程，学生将很难理解掌握.相反，如果教师讲解的同时，相应内容在屏幕上依次呈现，教学效果将较大提高.如介绍二重积分的概念时，计算曲顶柱体的体积，教师讲解用曲线网把xoy平面上闭区域分成n个小闭区域，以闭区域的边界曲线为准线，作母线平行于z轴的柱面，这些柱面把原来的曲顶柱体分为n个细曲顶柱体，从而当小闭区域直径很小时，细曲顶柱体可近似看做平顶柱体，从而n个平顶柱体的体积之和可近似看成整个曲顶柱体的体积.如果教师讲解这些后，再呈现细曲顶柱体的形成，学生很难在极短的时间里去理解教师的讲解内容与之后相应动画的一致性，相反，教师每讲一句话，同时在屏幕上呈现相应动画的形成，学生就很容易理解曲顶柱体体积公式的定义.

综上所述，大学数学多媒体教学设计可总结为：（1）文本和图片结合比仅文本学习效果更好；（2）排除多余的文字、图片及资源；（3）相关的文本和图片应放在一起，教师讲解的听觉文本或屏幕呈现的视觉文本应与相关图片同时呈现；（4）动画和视觉文本结合比动画和听觉文本结合学习效果更好；（5）动画和听觉文本两者结合比动画、听觉文本和视觉文本3者结合学习效果更好.

[1]谭本远.论高等数学教学中信息技术与教育技术的整合[J].数学教育学报，2005，14（4）：97-99.

[2]袁立新.关于高职院校微积分教学软件的基本思考[J].数学教育学报，2011，20（2）：65-68.

[3]Baddeley A.Models of Working Memory: Mechanisms of Active Maintenance and Executive Control [M].New York:Cambridge University Press, 1999.

[4]赵立影.基于工作记忆的多媒体学习设计[J].电化教育研究，2011，（8）：98-101.

[5]Paivio A.Mental Representations: a Dual Coding Approach [M].New York: Oxford University Press, 1986.

[6]John Sweller.Architecture and Instructional Design [J].Educational Psychology Review, 1998, 10(3): 251-296.

[7]Mayer R E.Nine Ways to Reduce Cognitive Load in Multimedia Learning [J].Educational Psychologist, 2002, 38(1):43-52.