认知发展研究新成果——David Tall的“数学三个世界”理论

周士民，聂立川，王 君

（1.青岛理工大学 基础部，山东 临沂 273400；2.河北农业大学 理学院，河北 保定 071001；3.哈尔滨学院 理学院，黑龙江 哈尔滨 150086）

关于认知发展理论的研究，皮亚杰、布鲁纳等教育学家在其著作中已经有深刻论述.进入21世纪，英国知名数学教育家Warwick大学教授David Tall在认知主义、建构主义基础上，融合了认知科学、新皮亚杰主义等相关研究于2004年提出了数学三个世界理论[1]，该理论是Tall关于认知发展研究的最新成果.

1 数学三个世界的理论基础[2]

该理论与认知主义、建构主义一脉相承，同时吸收了新皮亚杰主义、认知科学等研究成果而形成.

认知主义流派的代表人物有Piaget、Bruner、Skemp、Van Hiele和Fischbein等.Piaget认为抽象有3种形式：经验抽象、伪经验抽象、反思抽象；Bruner认为人用3种形式将经验转化为模型：行为的、形象的、符号的形式；Skemp认为人有3种性质不同的活动：感觉（输入）、操作、反思；Van Hiele认为儿童以格式塔方式认识对象，描述性质并定义出各种层次的图形，利用演绎推理推导出其它性质，形成理论体系.数学三个世界理论借鉴认知主义表征概念的方式：首先对现实对象操作，提取对象性质，逐渐上升为形象表征，再利用语言抽象出符号，最后通过严谨的定义和推理形成形式化公理理论.

建构主义下的APOS学习理论，将认知建构分为操作、过程、对象、图式4个阶段[3]；新皮亚杰主义下的SOLO分类理论，将认知发展阶段重新划分为：感知、形象、符号化、形式化、后形式化5个阶段，把认知看做是一个累积过程；建构主义与SOLO理论都承认了经验对形成认识的作用.数学三个世界理论受建构主义和新皮亚杰主义的启发，认为认知发展具有阶段性、层次性、累积性，David Tall还认为经验对认知形成有正反两方面的作用.

认知科学认为认知以联结的方式存在，重复能提高联结水平.脑科学研究表明，大脑中有专门的视觉区域感知事物，人先天具有识别、语言表达的能力，认知的形成与发展受大脑活动的影响，人类思维由具体向抽象过渡与大脑皮层活动相关.Lakoff认为所有思维过程在活动中都是具体化的.数学三个世界理论接受了认知科学的观点，认为人具有使用语言和模式识别的基本能力.因而有能力处理外部信息，并随着抽象程度的加深逐渐产生符号[4].

2 数学三个世界理论结构[5]

Tall在这里选择使用“界”不是指范围，而是指不同的思维发展方式.他认为人的认知过程是以“前集”与“前变量”为基础经数学三个世界而得以发展的.“前集”表示的是一种与生俱来的心理结构，该理论中特指“识别、重复、语言”；“前变量”即为个人以往的经验在大脑中建立的联结.

概念—具体化世界：现实中的具体对象与概念性具体都称做“具体化”的，即以对世界的感知为基础，通过反思利用语言形成精致的意义.在这个世界中，既包括对外部世界的认识，又包括对内部世界的感知.其数学学习对象是具体的、形象的、可见的，简称具体化世界.

过程—符号化世界：将操作压缩并用符号表示，进一步压缩形成概念的过程称为“符号化”的，即开始于过程操作，通过符号的使用实现由解决数学问题到进行数学思考的有效转换.在这个世界中数学学习对象具有符号过程性和符号概念性两面特征，符号过程性是指具体化数学世界的操作过程，符号概念性则是指通过对这个操作过程的概括、抽象等心智活动得到的数学对象，简称符号化世界.

公理—形式化世界：把利用形式化定义和证明建立公理体系的过程称为“形式化”的，即以对象性质为基础，通过高度抽象，主要是对符号世界进行自反抽象，发展为形式化定义，有时需要进一步证明，使之发展为形式化公理，简称形式化世界.

Tall认为，人以“前集”为生理基础，以“前变量”为社会基础，形成了数学认知发展的3种途径：具体化世界、符号化世界、形式化世界[13]，认知以感觉、操作和反思等基本活动为基础，经具体化、符号化、形式化的过程发展.

3 理论相关研究

3.1 关于矢量学习的研究[6]

Tall在研究矢量概念学习时完整地提出该理论.该研究以Lakoff具体化认知理论和Dubinsky的APOS理论为基础，在Amma Poynter关于矢量问题的研究启发下进行，继而不断发展和完善.研究采用先对“操作—过程”进行分析后对“操作－结果”进行分析的方式.研究认为感知/形象—具体模式和具体—符号模式是联系在一起的，从而把现实中的具体对象和概念具体联系起来.矢量的三个世界表征为：矢量在物理中有各种具体的表现形式，可以用有大小和方向的量表示；也可以用符号表示并规定运算法则；还可用矢量空间的形式化方式定义并把形式化运算作为公理.

3.2 数学三个世界之间的关系及大学数学学习研究

数学三个世界具有内在的、递进的发展方式[7]：具体化世界以对象特征为基础，通过观察、描述、定义对象性质并进行反思从而得以发展；符号化世界以操作为基础，将操作图式压缩，并用符号表示形成可想像的概念（thinkable concepts）；形式化世界以性质为基础，用集合理论定义，并通过形式化推理的方式发展.在教学中以“具体化”为前变量就直接用“自然化”的方法；以“符号化”为前变量会用程序的方法；以“形式化”为前变量会用逻辑的方法.同时Tall还发现具体化、符号化方法会影响形式化方法[8].就3者关系而言，认知发展以具体化、符号化为基础向形式化转化.原有的认知结构是通过与新情境融合的方式发展的，具体化、符号化、形式化在应用中实现融合，形式化会推动更高层次的具体化、符号化发展[9].体现出经验性和演绎性的辩证统一[10].

Tall分别在代数、积分和证明3个领域内[11]再次论述了数学三个世界的发展过程，同时提出了很多解决问题的方法.如用“局部线性”具体化方法[12]、“局部直”符号化方法、“ε-δ”以极限为前变量形式化方法理解积分概念.对于导数概念Tall引用Thurston提出的7种定义方法：（1）无穷小量法；（2）符号化法；（3）形式化方法；（4）几何方法；（5）比率；（6）近似；（7）显微镜法，即无限放大法.对于微积分内容Tall主张用感性的具体化和符号化的方法理解形式化概念[13].连续概念可以通过在电脑屏幕上画出宽为2ε高为2δ矩形，组成以x为中心的曲线连续动态图像；极限概念可以通过画一系列的点最后与极限值无法辨别时确定极限值；微分概念在“局部直”前提下通过高度放大曲线的一小部分看作直线，把dx和dy看成切向量的分量，df(x)是分量的商加以理解.对于函数h(x)=g(f(x))求导的链式法则可以用形象化的方法，Y=f(x)，Z=g(y)，在三维空间中以曲线的切向量（dx, dy, dz）为立方体的3边，分别向3个坐标面投影，dz/dx=(dz/dy)(dy/dx)实现对公式的理解.

3.3 数学三个世界下的认知发展过程研究

Tall认为，人通过感觉、操作、反思形成具体化世界；由特殊计算发展到一般计算并用符号表示，而后规定“算数规则”形成符号化世界；当数学由集合理论定义或由理论证明得出时，形成形式化公理世界[14].如图1[9]：

Tall同时提出了人的长期认知发展的结构理论[15].Tall认为人的认知发展以SOLO理论提出的累积性建构方式进行；认知在建立长期神经联结时，加强有效联结，抑制其它联结；数学认知经过抽象形成可想像的概念，而后经具体化、符号化、形式化发展，随时间推移成为高级形式；在应用该结构时将概念进行结构融合，建立可想像的概念间联系，形成一般图式[16]；将以前的概念结构重新组织会产生创造性思想，用具体化、符号化、形式化方式加以解决，从而使概念结构更加高级.

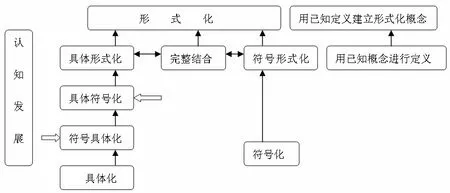
图1 数学三个世界下认知发展图

3.4 关于抽象 可想像的概念 结晶体概念的研究

Tall通过对3者的论述揭示出认知形成和发展的成因.由于人类大脑作用的范围限制，认识事物时人们必须将知识压缩后才能提取信息[17]，通过具体操作感知周围的事物，通过内部抽象形成特殊和一般认识.抽象可以通过认识对象的性质，将其分解成不同层次进而将其压缩；也可以对操作过程再认识，而后压缩成算术中的运算符号、代数中的公式符号、积分符号等；还可以先认识对象的性质，进行分阶段的压缩后，用集合理论和数学证明推导出其它性质，最终形成一个概念或公理体系，因此概念—具体化、过程—符号化、公理—形式化代表3种不同的抽象方式、3种概念形式、3种证明方式[18].

在“前变量”的影响下，人们通过操作认识事物，通过对本质联结的把握将知识压缩，并用符号表示形成可想像的概念，这是知识转化的关键[19].压缩途径可以Lakoff提出的分类方式，也可采用Dubinsky提出的APOS理论模式，亦可采用Tall提出的程序法即：程序—多个程序—过程—过程概念的方式，如图2[20]：

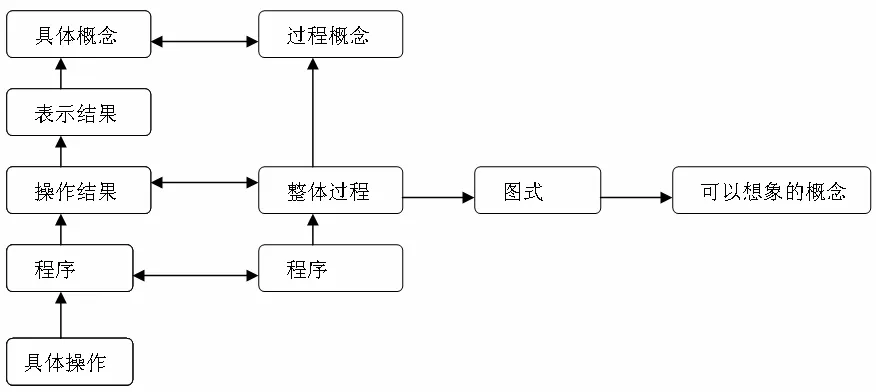
图2 将图式压缩成可以想象的概念过程图

为了合理解释抽象知识相互转化的原因，Tall于2011年提出了结晶体概念的思想.Tall认为当知识压缩形成一个内部实体后，会形成很多等价的概念和公理.他将结晶体概念定义为“一个特殊的知识结构，人们可根据周围环境确定它的必要性质，其他的概念和定理可以通过对其的推理而获得”[21]，它自身具有简约性、发散性的特点.例如完备的有序域是结晶体概念，因为任何两个满足完备有序域的公理都是同质的.

3.5 数学三个世界下教师的作用与教学研究

数学的三个世界认为知识是以联结的方式存在的，因此主张采用联结主义教学模式[22].该模式要求学生在学习中基于以前的经验做出合乎逻辑的假设，并通过积极主动地参与来完成知识的建构.而教师作为辅导者安排课堂活动，鼓励学生通过对本质概念的理解建立联结、分组探索、接受问题的挑战形成认识.教师通过准确把握知识、思维的联结点，使学生的探索逐渐深入；设置具有挑战性问题不断增强学生解决问题的信心和能力；通过学生间的互动交流使大多数学生基础更加扎实.该模式按照输入信息、激活信息、建立联结、提取和检索信息顺序进行教学.其优点在于充分调动了教师与学生的积极性，真正实现教学相长.

Tall带领的研究团队分别按照讲授法、联结主义教学法、发现教学法进行教学，经过一段时间后进行跟踪调查，并用国家课程测试进行测量，分为非常有效、有效、一般有效.所得数据显示那些主张用联结主义模式的教师教学效果最明显，那些主张用传授法或发现法的教学效果仅一般有效，坚持用折中方法教学的则大多数有效.因此，教师教学时要作为辅导者帮助学生将知识压缩成可想像的概念，并促使他们建立起知识之间的联结.如表1[22]：

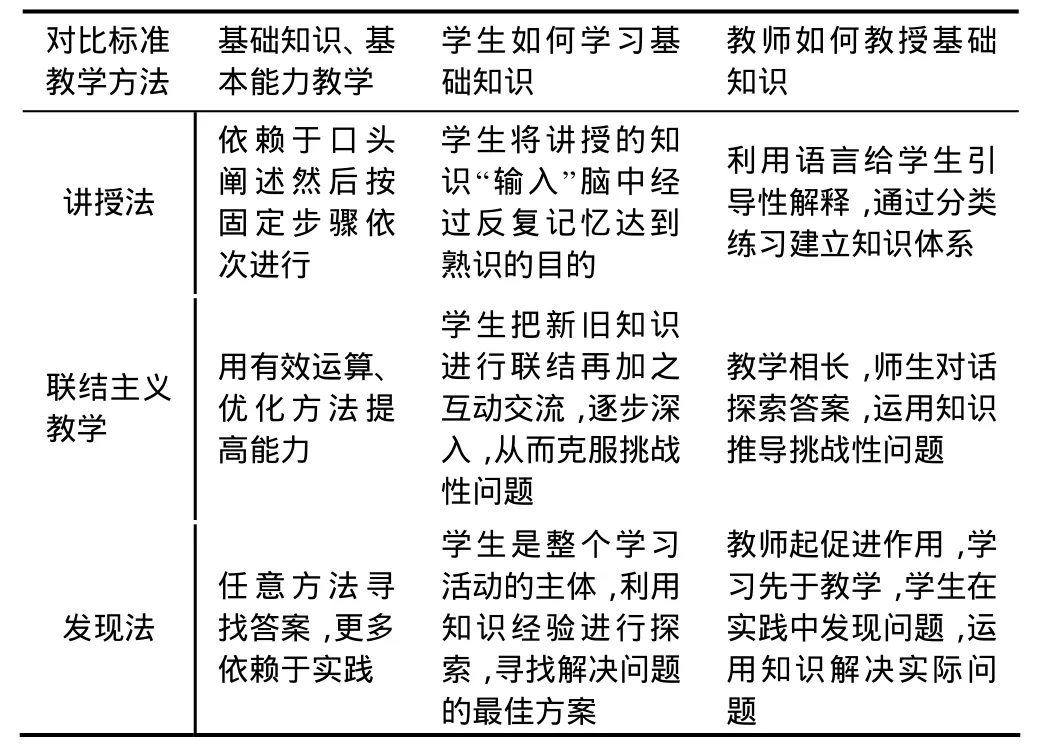
表1 讲授法和联结主义教学法及发现教学法的比较

4 数学三个世界理论的影响及创新

该理论的发展过程一直备受世界数学教育界关注.在2002年、2004年的两届国际数学教育心理学会议（PME）上，Tall分别作了题为“Embodied Action, Effect, and Symbol in Mathematical Growth”（见文[23]）和“Thinking through Three Worlds of Mathematics”（见文[2]）的报告.在2009年国际数学教育委员会议（ICMI）上，他的报告“Cognitive and Social Development of Proof through Embodiment,Symbolism and Formalism”（见文[14]）引起了与会专家们的极大兴趣.另外，2006年APEC筑波国际会议（见文[8]）、2007年APEC关于课例研究会议（见文[24]）以及2007年中东第三年度科学、数学、计算机教师会议（见文[22]）也都隆重邀请他到会阐述该理论的最新研究成果.同时，他所写的有关该理论的论文在国际数学教育权威杂志Mathematics Education Research Journal（见文[9，17]）、Journal of Mathematical Behavior（见文[25]）和For the Learning of Mathematics（见文[1，21]）等发表.在美国、英国、德国、澳大利亚、比利时以及台湾举办的数学教育国际会议上，Tall也就这一理论作了典型发言，引起了强烈反响.目前该理论处于结构相对稳定，内容不断完善阶段，并已经在日本、巴西、土耳其等国课堂教学中取得了很好的效果[1].由于该理论还没有得到全面推广，因此在世界范围内还没有形成一致评价，但是已经得到国际数学教育界同仁们的肯定和认可.

David Tall是这样评价该理论的：（1）该理论以儿童、中学生、大学生、数学家为研究对象，通过对人学习所有数学科目时认识规律的研究，揭示人一生的认知发展过程；（2）该理论对所有认知层次都起作用；（3）该理论作为一个整体去认识事物并形成结晶体概念.通过比较不难发现，皮亚杰研究儿童思维的认知发展过程，他把抽象作为认知发展的终点[26].而该理论研究抽象知识的形成和转化过程，把形式化推理作为最终目标，适合解释中学和纯抽象的大学数学知识的学习.同时，与新皮亚杰主义相融合，强调认知建构具有累积性、阶段性与层次性.建构主义认为，新知识的学习是以已有知识经验为基础的一个主动的意义建构过程[27].而该理论在承认经验对认知发展作用的同时，又说明了经验起的正反作用，指出在新环境下需要重新提取.相对于建构主义否认重复对认知发展起作用的观点[28]，该理论认为重复能加强联结并促进自动化操作的形成，体现出与认知科学相融合.该理论强调了符号在形成图式中的中枢作用，认为抽象知识以联结的形式存在并可以相互转化，因为知识压缩最终形成结晶体概念.它自身具有的推理性联结是抽象知识之间相互转化的根本原因[21]，弥补了APOS理论不能解释推理的不足.

2006年国际数学教育心理学大会（PME）承认，建构主义的影响正在消退，潜力已不再突出[29].数学的三个世界理论的出现给人们提供了研究认知发展的新视角，也可以重新审视学生的认知过程，以此创新教学理论、教学模式，并在实践中不断对其进行检验、修正.期待该理论对中国的数学教学改革，尤其对大学数学教学改革产生积极的影响.

[1]David Tall.Introducing Three Worlds of Mathematics [J].For the Learning Mathematics, 2004, (1): 1-11.

[2]David Tall.Thinking Through Three Worlds of Mathematics [C].Proceedings of the 28th Conference of the International Group for Psychology (PME), 2004.

[3]曹荣荣.APOS理论视角下无穷概念认知分析[J].数学教育学报，2010，19（1）：17-19.

[4]连四清，方运如.数学认知能力与语言认知能力的分离现象[J].数学教育学报，2006，15（2）：22-24.

[5]David Tall.A Theory of Mathematical Growth Through Embodiment, Symbolism and Proof [C].Plenary Lecture for the International Colloquium on Mathematical Learning from Early Childhood to Adulthood, Belgium, 2005.

[6]Watson, David Tall.The Relationship between Physical Embodiment and Mathematical Symbolism: the Concept of Vector [J].The Mediterranean Journal of Mathematics Education, 2003, (12): 73-97.

[7]David Tall.Embodiment, Symbolism, Argmentation and Proof [C].Conference on Reading, Writing and Argumentation at National Changhua Normal University, 2007.

[8]David Tall.Encouraging Mathematical Thinking That both Power and Simplicity [C].APEC-Tsukuba International Conference, 2006.

[9]David Tall.The Transition to Formal Thinking in Mathematics [J].Mathematics Education Research Journal, 2008,20(2): 5-24.

[10]曹一鸣，辛兴云.从数学本质解读数学课程改革[J].数学教育学报，2005，14（1）：42-45.

[11]David Tall.Embodiment, Symbolism and Formalism in Undergraduate Mathematics Education [C].Plenary at 10th Conference of the Special Interest Group of the Mathematical Association of America on Research in Undergraduate Mathematics Education, 2007.

[12]David Tall.Using Technology to Support an Embodied Approach to Learning Concepts in Mathematics [C].Cavatho L M, Guimaraes L C.Historia Technologia no Ensino da Matematica, 2003.

[13]David Tall.A Sensible Approach to the Caculus [C].Plenary at The National Meeting on The Teaching of Calculus,2010.

[14]David Tall.Cognitive and Social Development of Proof Through Embodiment, Symbolism, Formalism [C].ICMI Conference on Proof, 2009.

[15]David Tall.The Long-term Cognitive Development of Different Types of Reasoning and Proof [C].Conference on Explanation and Proof in Mathematics, 2006.

[16]David Tall.Cognitive Development of Proof [C].Plenary at The National Meeting on The Teaching of Calculus, 2010.

[17]Eddie Gray, David Tall.Abstraction As a Natural Process of Mental Compression [J].Mathematics Education Research Journal, 2007, 19(2): 23-40.

[18]David Tall.Differing Modes of Proof and Belief in Mathematics [C].International Conference on Mathematics:Understanding Proving to Understand, 2002.

[19]David Tall.The Transition from Embodied Thought Experiment and Symbolic Manipulation to Formal Proof [C].Plenary Lecture for the Delta Conference, 2005.

[20]David Tall.A Theory of Mathematical Growth Through Embodiment, Symbolism and Proof [C].Plenary Lecture for the International Colloquium on Mathematical Learning from Early Childhood to Adulthood, Belgium, 2005.

[21]David Tall.Crystalline Concepts in Long-term Mathematical Invention and Discovery [J].For the Learning of Mathematics, 2011, 31(1): 3-8.

[22]David Tall.Teachers as Mentors to Encourage Both Power and Simplicity in Active Mathematical Learning [C].Plenary at the Third Annual Conference for Middle East Teachers of Science, Mathematics and Computing, 2007.

[23]Anna Watson, David Tall.Embodied Action, Effect, and Symbol in Mathematical Growth [C].Proceedings of the 26th Conference of the International Group for the Psychology of Mathematics Education (PME), 2002.

[24]David Tall.Setting Lesson Study within a Long-term Framework of Learning [C].Presented at APEC Conference on Lesson Study in Thailand, 2007.

[25]Mercedes McGowen, David Tall.Metaphor or Met-before the Effects of Previous Experience on the Practice and Theory of Learning Mathematics [J].Journal of Mathematical Behavior, 2010, (29): 169–179.

[26]林敏，孙志凤.简评皮亚杰关于反省抽象及其发展研究[J].华东师大学报（教育科学版），2006，24（2）：66-71.

[27]周友士.基于建构主义的数学概念转变学习[J].数学教育学报，2004，13（3）：19-22.

[28]谢明初，朱新明.认知心理学视角下的数学教育[J].数学教育学报，2007，16（1）：12-16.

[29]徐文彬，喻平，孙玲.数学教育中建构主义三十年发展与反思[J].数学教育学报，2010，19（3）：1-6.