标准参照考试理论在高考中的应用——以H省2010—2012年高考理科数学为例

任子朝，王 蕾，朱乙艺，陈 昂

（1.教育部考试中心，北京 100084； 2.北京师范大学 教育学部，北京 100875）

1 理论基础和研究方法

高考理论上属于常模参照考试，一般都根据常模参照的理论进行分数解释，这已经是共识甚至是常识.近年来，国际教育测量领域出现一种倾向，通过对常模参照测验增加标准参照的分数解释，从而更为充分和有效地发挥考试对教育教学的反拨作用[1～2].对常模参照测验增加标准参照的分数解释至少具有以下两方面的好处：一方面可以促进高考这一社会考试发挥教育教学功能；另一方面有利于高考试题难度保持稳定.

研究应用IRT理论中的Rasch测量模型，假设考生对于试卷每个试题的反应都受其能力的支配，并建立合适的数学模型来描述它们之间的关系，然后通过对模型中的各个参数进行估计，包括描述考生的能力水平参数以及用来描述试题性质的难度参数，使得考生能力和试题难度分离，进而建立一个等距量尺，从而用不同的试题难度来测量不同学生的能力值.

研究还对试题进行了等值处理，具体做法是首先同时通过“锚题”和“锚人”的等值设计来使2010年、2011年和2012年这3年的高考理科数学建立联系，然后综合采用同时校准和锚定参数的方法来使估计出来的参数值置于同一量尺上.这样通过等值设计和Rasch模型就可以把来自不同试题试卷版本的考试分数转换到同一个分数系统上，以使得当考生参加测量同一种知识和能力考试的不同试题试卷版本后，其所获得的分数可以直接进行比较，不会由于不同版本难度上存在差异而引起不公平的现象.

在标准参照分数解释的框架下，研究还借鉴了标准设定（standard setting）的方法，将能力等级标准分为5级、4级、3级、2级、1级和1级以下，将考生和试题都归入相应的级别，细化了对考生和试题内部结构的研究.

研究应用Rasch模型，以一个省（H省）的高考理科数学实际考试数据为基础，研究了不同年份试题的难度分布、考生的水平变化情况，并且对各能力成分进行了分级处理.

2 标准参照考试理论在高考中的应用

2.1 考生能力分布和试题难度分布概览

H省2010－2012年高考理科数学考生能力与试题难度分布图见图1.

图1中各年份的左侧条形图表示当年高考考生能力分布情况；各年份的右侧表示当年高考试题难度的分布情况.图中的3年的考生能力和试题难度是在同一量尺上测量出来的，因而可以进行直接比较.通俗地说，这些题目就像是量身高的尺子的刻度，通过这样一把固定的尺子就能够客观地测量考生的能力.只要接着做好等值设计，以后该省的高考理科数学都可以接着放到这个量尺上来测量，这样就可以实现高考跨年度的纵向直接比较.

从图1中可以看出，2010－2012年该省理科考生数学能力呈较明显的正态分布，理科学生的数学能力总体上呈现下降的趋势，但这种变化趋势还需要进一步的数据和研究加以证实.3年试卷CTT难度均值分别为0.41、0.41、0.34[3].应用等值处理后，3年试卷的Rasch难度均值分别为0.297，-0.053，-0.130，3年考生的能力水平均值分别为-0.108，-0.452，-0.783.从上面的分析可以看出，这3年的考生的能力是逐年下降的，3年试卷的Rasch难度也是逐年下降的，但是3年试卷的CTT难度却是稳中有所上升，之所以会出现这种情况，是因为试卷CTT难度的变化受考生和试题两个因素的相互影响，而试卷Rasch难度不受考生能力因素的影响.

2.2 考生能力分等

图1只是形象说明了3年考生能力水平的变化情况，但具体各层次的考生是如何变化的还不精确.为了更具体精确地了解H省理科数学2010—2012年的考生能力等级结果及其变化趋势，研究以2010年的考生为基点，将考生按能力水平从高到底排列，分别选择5%、25%、50%、75%和95%分位点，作为能力层级的分界点，将能力等级标准分为5级、4级、3级、2级、1级和1级以下，对应的考生logit（逻辑单位）位值分别为0.95、0.38、-0.08、-0.53和-1.26.根据以上的分等画成能力等级分布图，能力等级分布图描述了省考生群体的能力分布情况，可以实现不同年度之间各等级的对比.图2展示了H省这3年的各年度的各能力等级的考生群体在总样本中所占的比例，图中纵轴表示百分比，0点以上描述的是2级和2级以上等级的百分比；0点以下描述的是2级以下等级的百分比.不同的颜色区间表示不同的能力等级所占的百分比.从图2可以直观地看出H省的理科学生的各等级能力所占百分比在3年中的变化情况，即从2010—2012年，1级及以下等级所占的比例总体上逐年递增，1级所占的比例逐年递增，1级以下所占的比例逐年递增，2级所占的比例逐年递增，3级所占的比例逐年递增，4级所占的比例逐年递减.

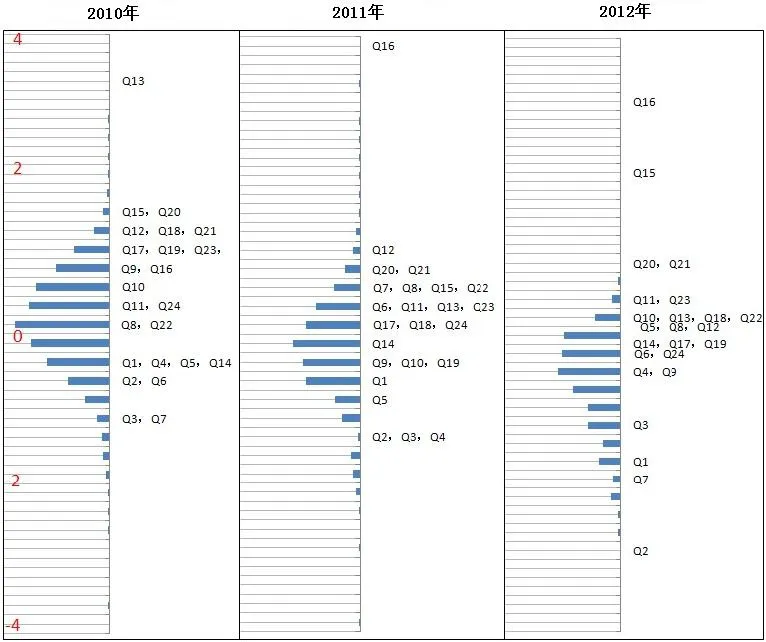
图1 H省2010—2012年高考理科数学考生能力与试题难度分布

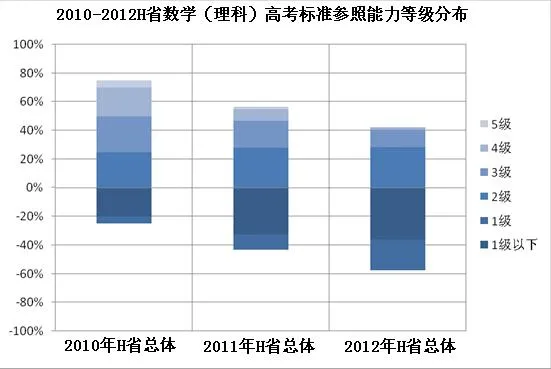
图2 高考数学（理科）标准参照能力等级分布

2.3 试题在能力层级中的定位

各种考试都有各自的能力要求，并且这些要求在试题中体现出来.美国SAT I 主要考查推理论证能力，SAT II 主要考查数学学科能力[4～5].中国的高中数学课程标准以原有的教学大纲为基础，划分出了7种数学能力[6].高考数学科所考查的能力分为逻辑思维能力、运算求解能力、空间想象能力、数据处理能力和创新应用能力5个维度[7].高考命题中，按照学科能力划分的不同维度，通过设立标准参照下各能力分级，根据试题的Rasch难度值进行等级分类，对高考的所有试题在能力等级中做出定位.

表1对2010—2012年H省高考数学（理科）试题按照所考查能力维度和所在的能力等级进行了相应的定位.

在《高考数学能力层次和考查效度研究》[8]中，研究了高考数学各个能力之间的层次关系，其基本结论是创新应用能力是在基本数学能力的基础上更高层次的能力.文中的能力层级是指单一能力中，不同级别的差异.如可以将逻辑思维能力分为5个层级，分别研究考查各个层级试题的特征.因此约定，能力层次是指各种能力之间的关系，能力层级是指同一能力中，不同级别间的关系.

分析表1可以得出如下的结论：3年各种试卷所考查的能力成分基本稳定，不但各种能力考查的比例相近，而且每一能力所要求的层次及各层级的比例也相近，说明试卷稳定、信度很好.各种能力考查的层级符合考试要求，与考生 的水平基本匹配.

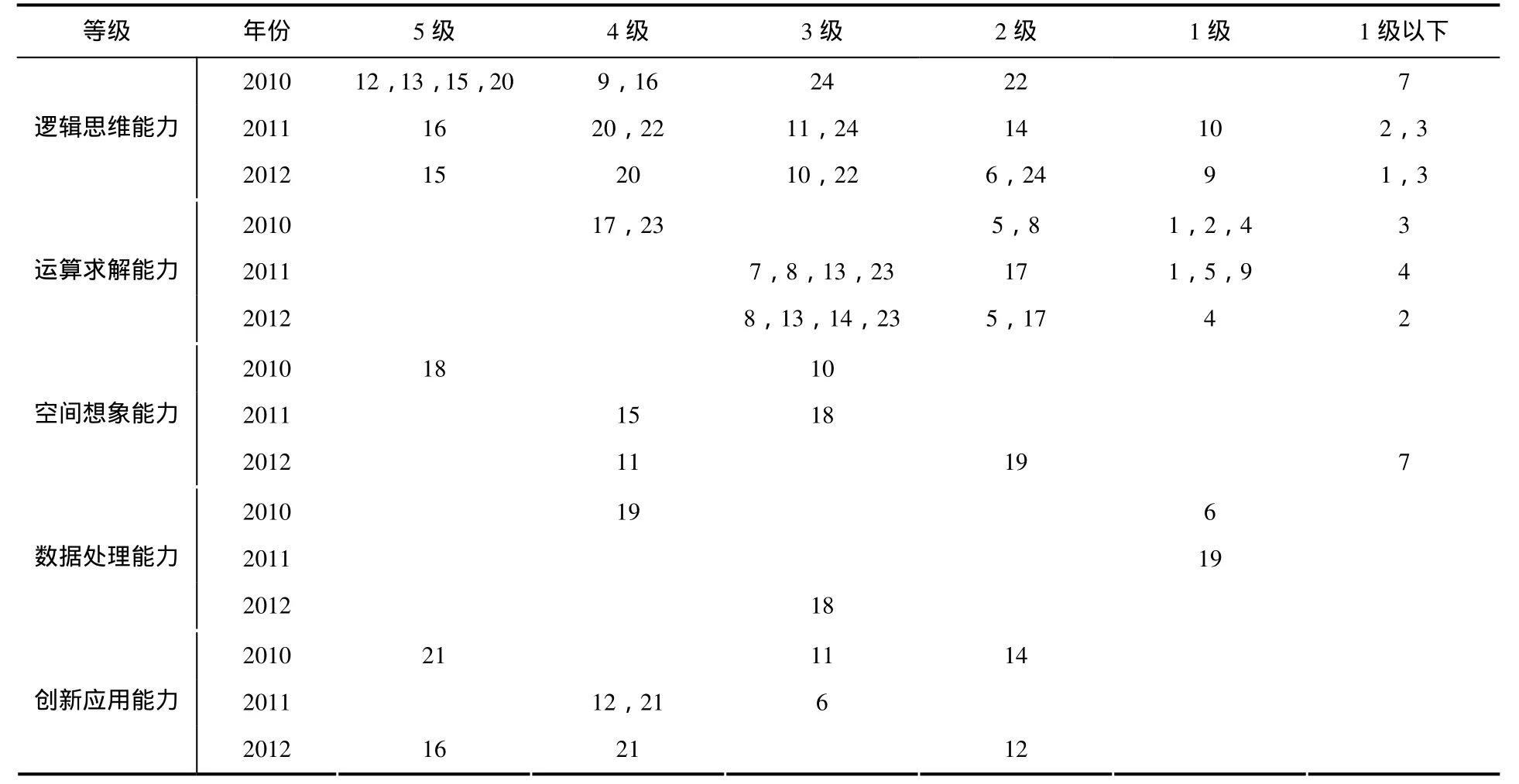
表1 2010—2012年H省高考数学（理科）试题在能力等级中的定位

根据《高考数学能力层次和考查效度研究》，创新应用能力是更高层次的能力，逻辑思维能力本身对数学成绩的贡献在所有能力中是最大的，在加上逻辑思维能力通过创新应用能力的间接贡献，逻辑思维能力本身对数学成绩的贡献在0.44左右.在实际考查中，对这两项能力的考查都达到了4级或5级的水平，这是符合能力考试要求的，重点能力，重点考查.

实际考查中对运算能力和数据处理能力的要求一般在3级以下，因为运算能力和数据处理能力属于基本能力，对其要求也应合理，一般控制在基础要求.对这两项能力的过高要求会导致试题的繁琐和雍长.

从上面的分析可以看出，高考对各种能力成分的考查层级符合考试大纲的要求，并与考生水平匹配.

2.4 考生性别偏差分析

考试公平的理论涵义应是考生的成绩只与考查的能力和知识有关，而不应与其社会经济背景等人口统计变量有关.中国是个多民族大国，改革开放形成了不同的利益群体和社会层级，考试工作者有必要关注不同子群体的考生差异，及时发现和预警值得注意的问题，避免由于不公平现象的大量涌现而给和谐社会造成影响.

利用考生报名表和问卷调查，大量的考生背景数据被保存在数据库中，使考试题目性能偏倚分析（DIF）等成为可能.图3为2012年H高考数学（理科）所做的性别DIF检验，男、女生的差异为0.16逻辑单位，表明数学试卷对男、女生不存在功能偏差.

3 试卷能力水平分析

建立能力量表，可以进行群体之间的能力比较.但是要想实现不同年份间的试卷原始分等值，还需要更复杂的计算.通过引入期望得分的概念，建立了不同年份之间原始分数转换表的模型.能力值为iθ考生期望得分为：

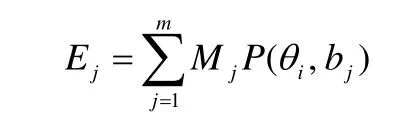
其中，Mj为题目j的原始分数，P(θi,bj)为能力值为θi的考生在题目j上的得分概率，bj为题目j的Rasch难度.对于只含有二级计分题目的试卷而言，此公式可以直接用来计算期望得分；对于含有多元计分题目的情况，公式需要进行更复杂的变换.

通过计算能力值logit在[−4,4]的考生期望得分，并且进行年度之间的对应转换，得到2010—2012年该省高考数学（理科）经过等值后的原始分数对应图.（见图4）

图3 2012年H省高考数学（理科）性别DIF检验

图4中横坐标表示考生能力logit的取值，范围为[−4,4]；纵坐标表示考生能力值所对应的试卷期望得分.从图中可以看出，考生各能力值所对应的试卷期望得分基本吻合，说明3年试卷对能力的要求程度基本稳定.特别是对能力水平比较高的考生，相同水平的考生其在3年的原始分数基本相同.

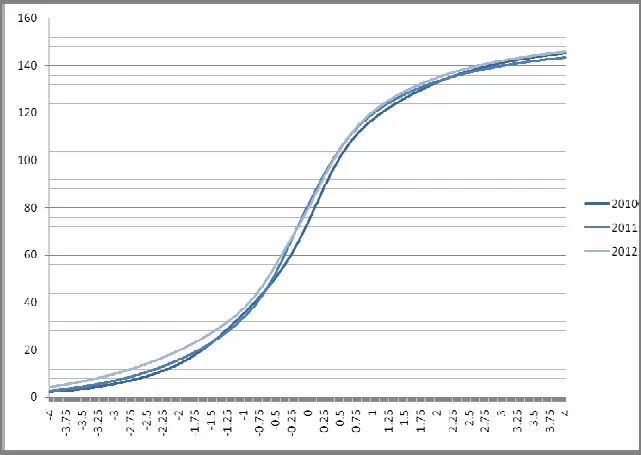
图4 2010—2012年H省高考数学（理科）等值后的原始分数对应图

另外，根据得到的原始分数对应图，可以进行任意两个年度之间的分数的等值转换.例如，可以把2011年和2012年的原始分数通过此图等值到2010年，从而进行3年之间分数的比较.从表2可以看出，在4、5级的水平，3年原始分数的差距在3分左右，说明试卷对高水平能力的考查比较稳定.在2、3级水平，3年的原始分数差距逐渐增大，达到7分左右，说明试卷对中等能力的考查要求有所变化.而在1级水平，3年的原始分数差距又缩小.

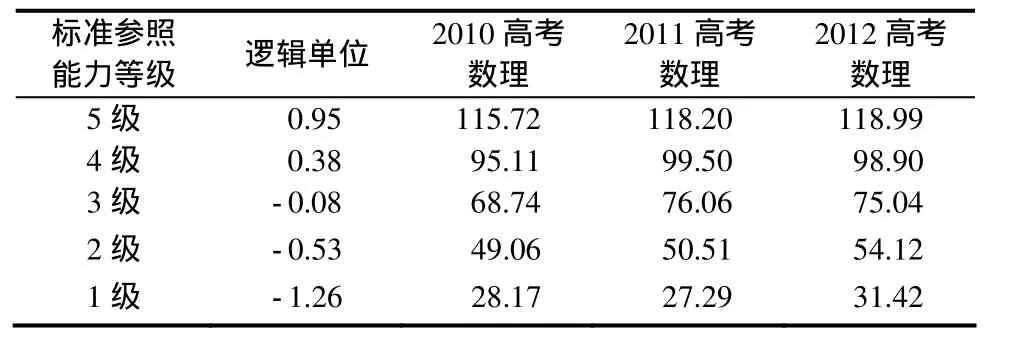
表2 标准参照能力等级与原始分对应表

4 结 语

通过对统计数据的分析，可以得出如下4个结论：

（1）应用等值分析的方法可以监测考生水平的变化情况，为命题提供预警.同时也可以检测试题水平的变化，为评价提供科学的依据.

（2）高考理科数学试卷的能力水平的要求基本稳定，同一能力水平的试卷原始分差距较小.

（3）数学试卷对男、女生不存在功能偏差.

（4）各能力成分的层级要求科学合理，年度间能力层级的要求基本稳定.

在发挥传统大规模教育考试原有的选拔功能外，从技术上对其加以改造，使之成为客观等距量尺，可以实现对不同年度或不同次的考试结果进行科学的比较.更进一步，基于增值评价的理念，通过构建同一学科的共同能力量表，可以摆脱传统考试一次性处理的局限，实现对教学过程的增值评价，引导教学和研究人员科学分析考试结果的变化，诊断学业中存在的问题，促进教育教学良性发展.

[1]王蕾.拉什测量原理及在高考命题评价中的实证研究[J].中国考试，2008，（1）：32-39.

[2]王蕾.PISA的教育测量技术在高考中的应用前景初探[J].清华大学教育研究，2012，33（3）：105-111.

[3]教育部考试中心.高考理科试题分析（课程标准实验）（2010—2012年）[M].北京：高等教育出版社，2010—2012.

[4]张紫茵，马小刚.美国SAT数学考试述评与启示[J].数学教育学报，2011，20（6）：60-62.

[5]廖运章.述评美国高中数学焦点[J].数学教育学报，2013，22（1）：65-69.

[6]袁智斌.对《普通高中数学课程标准》文本的反思性解读[J].数学教育学报，2009，18（6）：78-84.

[7]教育部考试中心.普通高等学校招生全面统一考试大纲的说明[M].北京：高等教育出版社，2012.

[8]任子朝.高考数学能力层次和考查效度研究[J].中国考试，2012，（7）：3-8.