“经验之塔”与体验性网络课程——数学方法论课程的实践研究

张映姜

（湛江师范学院 数学与计算科学学院，广东 湛江 524048）

数学思想方法是数学的精髓、灵魂.数学学习不仅仅是知识的学习，更是数学思想、数学方法的学习.思想方法是数学教学的基本原则.湛江师范学院开设了《数学方法论》课程.期待增强高师学生对数学思想方法的理解，增强思想方法对数学教学内容的组织，促进数学解题策略的形成，丰富师范生数学经验，有效地促进高师学生的教师专业成长.思想方法不同于数学知识，数学思想具有观念性特点，数学方法具有程序特征，由于受传统教学媒体的局限，课堂上很难展示经典案例的生动性，较难展现方法的程序性、过程性，学生活动参与性较弱.如今，网络媒体为《数学方法论》学习提供了较好条件，戴尔的经验理论为教师选择合适的媒体资源、采用恰当的课堂学习方式提供了某些参考的理论依据.多年的《数学方法论》教学实践说明，交互式的动画、可参与的网络实验等是课程《数学方法论》学习的重要资源，经典的案例凝聚了历史文化，创设了浓郁的数学文化情境，高师学生参与性增强了，学习体验增加了.这些是传统教学媒体无可比拟的.

1 戴尔的“经验之塔”理论

数学思想、方法是主观对客观规律的反映，是对客观世界一般规律的概括和总结，但仍离不开人的主观经验.对数学思想方法的认识终究是人的认识，离不开实践活动.波利亚认为，学生的学习从经验开始.“大多数最美妙的数学灵感来源于经验”（冯·诺依曼）.“我们真正的老师是经验和感觉”（卢梭）.这充分说明经验在学习中的重要性.许多专家相当重视数学经验，尤其是数学思想方法方面的创新活动经验.只有当数学思想和数学知识作为一个环节归入个人经验时，才能被理解和掌握.所获得的数学方法的经验影响数学知识的组织、策略的运用以及对数学的认识，也将影响高师学生的教师专业成长[1].

“经验之塔”理论认为，学生的学习经验可分为做的经验、观察的经验、抽象的经验.如图1，学生“做的经验”处于“塔”的底部，是最直接、最具体的经验；其次是观察的经验，位于“塔”的中部；立于“塔”顶是最抽象的经验，

即视觉、言语符号的经验.学习从直接经验开始，并由具体经验到抽象经验.但学习并不总是遵循从直接经验到间接经验.戴尔的经验理论也不能解决技能的训练问题，智慧技能和动作技能需要亲自操作、反复训练才能形成经验、熟练掌握；电子的虚拟操作替代不了黑板、白纸上的推演，电脑演示替代不了真实的科学实验[2].多媒体技术、网络信息技术在20世纪末才得到广泛运用，戴尔《视听教学法》中的“经验之塔”理论不可能预见动画图片、网络实验等媒体对学生知识经验的促进作用.现代媒体毕竟是高师学生获得知识经验的重要方式之一.尤其是，当不能获得思想方法的直接经验又不能较好地形成思想方法抽象经验时，可参与交互的网络实验、互动的动画、表现力强的媒体模型等能让学生获得具体的、间接的替代经验.网络信息资源远远不只是提供形成“观察”经验的学习媒体，在很大程度上还提供形成“做”的经验以及“抽象符号”经验的学习媒体.

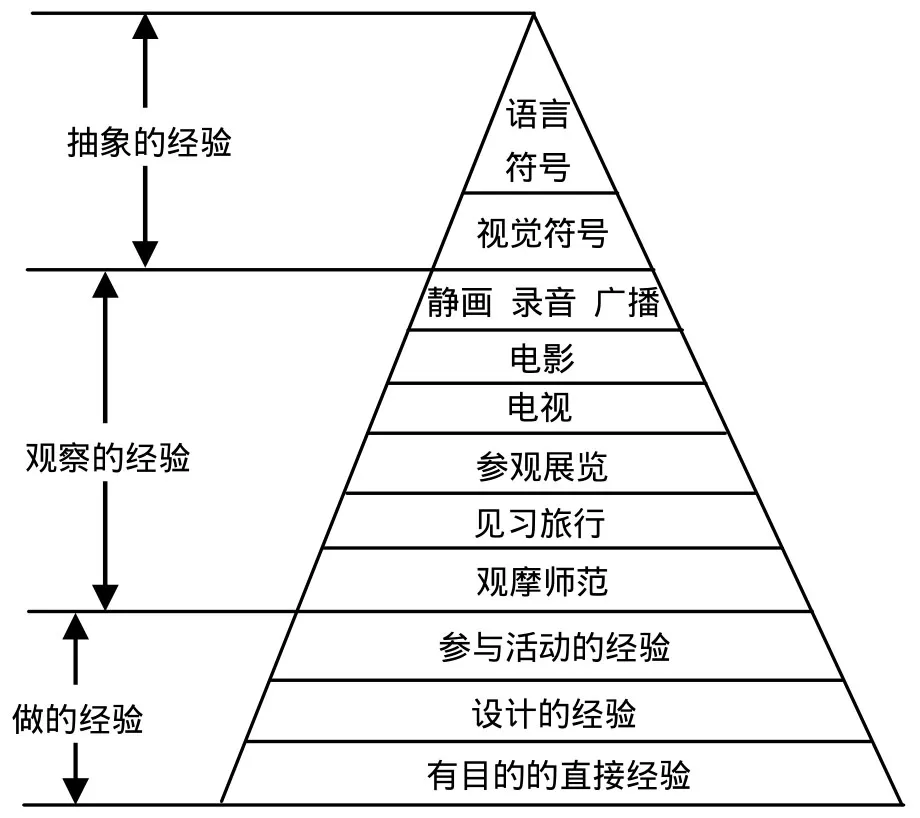
图1 经验之塔[3]

2 丰富数学方法经验的网络资源

戴尔的经验理论对于课程《数学方法论》学习资源的选择具有指导作用.经验来源于实践、源于体验.教育是经验的改选重组.数学的思想方法以数学经典案例为载体，通过网络资源进行传递.网络媒体资源实现数学思想、数学方法可视化、操作化，使高师学生有了直观生动的认知体验，更深入地理解数学思想方法的涵义，更好地获得思想方法的经验，并使经验具体化.数学变换借助七巧板几何图形的变换、函数图象的变换等进行学习，理解数学变换方法；迭代法的学习借助河内塔实验、勾股树等经典案例进行.类比法通过三角形与圆等图形的类比、棱锥与球等图形类比进行学习.数学归纳法的理解、掌握需要通过多米诺骨牌的（网络）视频，生动再现数学归纳法的初始条件及递推关系.现代媒体往往能提供数学经典案例，形式多样的、生动直观的网络素材，能供参与的网络资源，虚拟参与得到“直接经验”，通过观察获得“间接经验”.具体地，主要有3种网络学习资源.

2.1 能形成“做的经验”网络交互资源

通过网络系统的虚拟场景增强教学媒体的真实，为高师学生构建可视化的“真实场景”.这种可视化的“真实场景”能让高师学生获得与真实生活中相似甚至相同的认知体验，获得“做的经验”.网络上共享的七巧板的拼图、抛硬币的实验、函数图象的变换等资源可人机交互，动手操作，参与活动，进行观摩示范，以及数学设计.通过这些可参与的网络资源，亲手点击鼠标，亲自拼一拼，试一试，体验思想方法.让学生摆一摆，拼一拼，探索数学方法的规律.让学生“做中学”、“玩中学”，改变“听中学”、“看中学”的学习形式，让学生获得“直接经验”；特别是可交互的网络资源，给学生提供动手实践的机会，增加做的环节，容易产生最直接的、难以忘记的学习经验.交互的学习资源能促进学习过程中高师学生的深度参与.

2.2 能形成“观察的经验”的图形资源

观察是重要的学习活动.戴尔认为，经验源于观察.实践表明，许多经验来自于观察，观察依赖于情境，即经验源于情境中的观察.特瑞赤拉曾证实：83%的信息通过视觉获得.视觉获得的经验信息最多.“一切知识都从感官开始的”（夸美纽斯）.人类获得更多的是间接经验.高师学生通过几种感官交互，获得思想方法的“观察经验”，有了身临其境的认知体验.观察活动有助于对数学思想方法经验的获得.网络能提供许多便于观察的资源.生动活泼、形象直观的网络图片展示或简洁明快的网络视频，提供学生观察的机会，获得观察的经验；如图解、模型、图表、示意图，这些视觉符号有助于学生的观察，利于抽象经验的进一步形成，图片、动画等形象生动具体，便于观察，丰富学生的观察经验.利用图解、模型、图表、示意图等直观图形，构建知识学习的直观情境，把抽象的知识化为具体、形象的、可感知的东西，把学习内容、对象展现在学生面前，让学生帮助学生理解概念，通过多种外部刺激迅速感知知识，形成形象性知识，使抽象知识具体化、过程化，深奥的知识形象化、趣味化，让学生通过多种刺激迅速感知知识，把握知识的意义，形成生动的知识，促进学习迁移.

2.3 历史悠久的经典案例能形成数学方法符号经验

数学的历史文化影响学习经验的获得.文化是通过教育进行传承.文化的教育归根结底是关注人的发展，重视人的因素.社会文化因素影响观察的视野.爱因斯坦说，“正是理论决定什么是可以观察的.”历史的沉淀形成了人类丰富多彩的文化.知识的历史文化性无疑促进学生观察、体验及经验的获得.所以，历史文化体验是数学思想方法经验的又一个特色.抛硬币的实验、七巧板拼图等，都是数学上的经典案例，它们浸润着数学悠久的历史与纯美的文化，成为数学方法论的学习资源，引导学生活动思考，欣赏数学文化，品味悠久历史，获得数学经验，丰富方法内涵.学生通过体验性学习活动，增强学习体验，形成并强化数学知识经验.

3 经验理论下数学方法的网络学习方式

网络信息、多媒体技术为数学思想方法的学习活动给予了充分的支持.经验理论是数学思想方法网络学习遵循的主要依据.通过网络学习资源，让高师学生既可获得“观察的经验”又可获得“做的经验”，并进一步促进“抽象的经验”的形成，实现了思想方法在“做、观察、抽象”3种层次经验的交融，实现高强度的认知刺激和最大限度的体验，拓展数学创造性思维，达到了更有效的学习效果.利用网络学习资源，学生直接参与，获得具体经验，丰富做的经验，或通过图象观察获得替代经验；或通过符号的学习，获得符号表示的经验.操作探究、设计学习，学生获得直接经验；示范观摩、案例学习，学生获得间接经验.通过体验性学习活动，进行概括总结获得数学方法，丰富学生个体知识的内涵，完善知识的涵意，掌握数学方法，实现学习目标.

3.1 探究学习

数学研究、学习需要探究、探索，“在人的心灵深处都有一种根深蒂固的需要.这就是希望自己是一个探索者、发现者、研究者，而在儿童的精神世界中这种需要特别强烈”（苏霍姆林斯基）.实验法、归纳法、类比法等数学方法的运用是探究学习的有效方式，是在活动中领悟数学方法.探究学习既可以满足学生对探究的需要，同时又可以帮助学生对数学方法的运用和理解.网络上有许多共享的数学实验是课程《数学方法论》探究学习的经典案例.如图2，这是抛硬币实验.通过抛硬币的实验，学生能认识随机实验的特点，并能解决日常中难以处理的大样本随机实验研究问题，也有助于学生理解随机观念.通过实验探究，学生能发现随机现象中固有的数学规律，掌握概率思想.利用网上实验资源，可以让学生进行实验、归纳、类比等活动，学会探究学习，有了探究的经历，满足探究的欲望，获得做的经验，在活动中进行体验性学习，掌握了数学方法，有了创造性数学活动的经验，提高数学能力.

3.2 动手操作

动手操作是形成思想方法间接“做的经验”的重要方式，这也恰好发挥了增强虚拟情境真实性的网络优势.如数学变换方法包括几何图形的平移、旋转、对称，以及函数图象对称、位移、伸缩等变换.利用网络中共享资源参与交互，动手操作，在进行几何变换、图象变换操作中掌握、理解数学方法，获得“直接”经验，验证数学结论，提高学习兴趣，强化学习动机.为了理解变换思想，可利用函数图象的对称变换进行认识，研究函数y=f(x)与y=−f(x)，y=f(x)与y=f(−x)，y=f(x)与y=−f(−x)图象变换情况，学生亲自参与，人机交互，如图3.y=f(x)与y=−f(x)，y=f(x)与y=f(−x)图象分别关于x轴、y轴对称，y=f(x)与y=−f(−x)图象关于原点对称.学生分析思考后，发现，这3种函数图象的对称变换对于点的坐标的影响只是横、纵坐标符号的变化，最终概括为关于轴对称或点对称两类.学生思考函数图象或几何图形变换，就能发现数学变换方法的规律.特别是参与操作、动手交互.听过的可能会忘记，看过的可能会明白，但动手操作过的肯定不会忘，并能深刻地理解、准确地掌握，获得生动的经验.对照几何图形变换、函数形式的变化，就能获得几何变换的经验，增强几何图形经验的直观性、生动性，丰富学生的几何联想，体验数学活动，也获得数学变换的“替代”经验.

图2 抛硬币试验

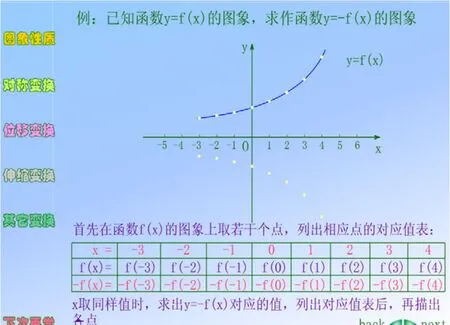
图3 函数图像

3.3 观摩示范

依戴尔的“经验之塔”理论，示范观摩是高师学生获得数学思想方法间接经验的重要方式.对课程中的尺规作图、对称、化归等方法，观摩示范也是一个有效的体验学习方式.利用网络资源中动画、图片、图表、挂图、幻灯、录音、录像、电影、图解、模型、示意图等进行示范，展示操作过程，让学生进行仔细观察，反复模仿，使学生掌握方法运用的程序，领会数学方法的规律，获得操作的替代经验.观摩示范，既能使学生获得丰富的感性经验，加深对事物的印象，又可以激发学生的学习兴趣，发展学生的观察力，加强技能的掌握、理解，增强记忆效果.

如图4，网络资源中的图案设计（www.diyifanwen.com/kejian/chuzhongyinianjishuxuekejian）.赏心悦目的图案如何制作？图案的制作展现了尺规作图的方法，用形象、直观的、交互式的动画方式，用图案制作示范尺规作图的程序和方法，展示图案制作过程，如图5.通过操作示范，让学生亲眼看一看，亲自做一做，观摩图案的设计思路，观察图形制作方式，发现图形制作奥秘，掌握几何尺规作图的方法，获得替代经验.

图4 图案设计

图5 图案制作过程

3.4 数学设计

数学设计也是高师学生获得数学思想方法替代经验的重要方式，能有效地提高创造能力.李约瑟说，七巧板是“东方最古老的消遣品”，“其变化之式多至千余.体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之”.拿破仑流放时利用七巧板打发时光.七巧板的拼图游戏能体现数学的平移、旋转等变换方法.如通过七巧板的数学设计活动，不仅吸引注意力，激发学习动机，增强参与、创造的意识，而且还在拼图过程中理解其中所运用的几何变换方法.利用网络资源中七巧板设计的平台，进行七巧板的创作，用七巧板拼成吉祥图案，庆贺节日，游戏娱乐.变化丰富，巧妙搭配，千姿百态.通过7块板的平移、旋转等几何变换，进行数学设计，拼出袋鼠图案，如图6.通过七巧板中5块三角形、一块正方形以及一块平行四边形的平移、旋转等几何变换，进行精巧的数学设计，既能体验几何变换的思想，获得变换方法运用的经验，也能动手设计，培养创新意识，拼出精美的几何图案，感悟数学创新.当然，也体验七巧板的历史文化.

图6 七巧板

3.5 案例学习

案例学习是根据特定的要求，对数学中经典的实例进行研究，达到理解知识、掌握方法、获得体验的一种方式.针对数学的无穷小方法、类比方法，通过数学中一些经典案例的研究、学习，展示巧妙的技巧，突出鲜明的主题，欣赏解决策略，体验创新的经历，获得替代经验，从而理解数学思想的精髓，掌握数学方法.案例越经典越好，经典案例有醍醐灌顶的效果.利用经典的案例把学生的学习注意力集中在有趣的论题上，通过生动事例的再现，突出中心论题，反映现实生活场景.这样，案例就成为传递数学概念、数学原理、数学方法、数学家情感的重要方式.通过网上经典的历史文化案例，如把圆等分割成全足够多个小扇形，近似于三角形，再拼成一个近似矩形，如图7，猜测出圆的面积公式，从而展示人类思考的方向，欣赏、体验人类高超的智慧.或利用三角形与圆的类比，如数学家开普勒一样思考，如图8，把长为2πr的圆周n等分，每份长Δ，周长ΣΔ=2πr，当n取相当大的整数时，得到n个高约等于半径r的近似于三角形，每个近似的小三角形面积为S=Δr；再对所有近似i小三角形进行面积求和∑S=Δr.i

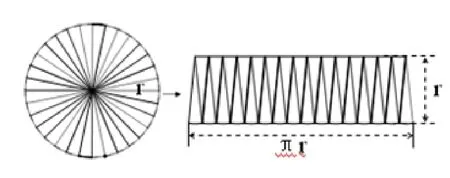
图7 圆的公面式积推公导式推导

图8 图圆与8 三 圆角形类比

于是，得到圆的面积公式

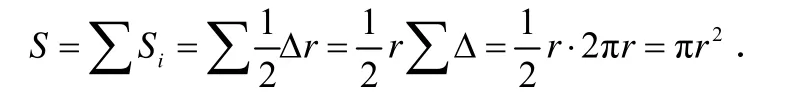
并由此体验微积分的思想：无限分割—三角形面积—求和—极限[5].类比上述方法，还可类比锥体体积公式，求得球的体积.类比锥体求得球的体积的经典案例学习，能让人们充分体验到无穷小方法用于求面积、体积的积分学的思想，展示数学家求旋转体体积的精巧的思路和方法.通过典型案例进行研究学习，学生在经典案例的文化情景中，掌握思想方法，领悟问题解决的策略，增强想像力，拓宽数学视野，激发或强化学习动机，保持浓厚兴趣，形成独到的见解.

[1]胡典顺.数学经验主义及其对数学教育的启示，数学教育学报，2012，21（4）：1-4.

[2]王绍铭.经验之塔前的思考.中国电化教育，2006，（7）：20-21.

[3]耿新锁.戴尔的“经验之塔”理论及其现实意义[J].教育史研究，2003，（6）：68-71.

[4]顾越岭.关于构建数学方法论理论体系的探讨[J].数学教育学报，1998，7（1）：53-57.

[5]罗志华.重温圆的名题，体验数学文化[J].数学教学研究，2010，（8）：15-18.

[6]曹才翰，蔡金法.数学教育学概论[M].南京：江苏教育出版社，1989.

[7]钟启泉，汪霞，王文静.课程与教学概论[M].上海：华东师范大学出版社，2004.