侗族数学文化面面观

2013-11-01罗永超

数学教育学报 2013年3期

罗永超

（凯里学院数学科学学院，贵州凯里 556011）

1 概述

随着数学课程改革实施的深入，国家、地方、学校三级课程的需要日显凸现，迫在眉睫.为了贯彻落实国务院三级课程管理政策的精神，以有效提高课程为当地经济服务的适应性，促进教育与当地经济社会发展紧密结合，满足少数民族地区数学教育的需要，项目组近几年积极组织师生收集、研究和挖掘少数民族数学文化，其目的是弄清少数民族数学文化背景，了解少数民族学生学习数学的基本思维方式，适时地在少数民族地区实施跨文化数学教育.在此，仅报告项目组对侗族数学文化部分的研究成果.

侗族是全国55个少数民族之一，主要分布在黔、湘、桂3省区的毗邻地区，全国侗族人口约三百万.侗族没有文字，长期生活在相对封闭的山区，山外的文明至今没有将他们同化，世界乡土文化基金会将贵州省黔东南苗族侗族自治州列入“返璞归真，回归自然”的十大旅游胜地之一，并称侗族文化是世界文化的瑰宝，是“隐藏千年的文明”，称侗乡是人类仅存的“人与自然和谐之地”、“人类疲惫心灵的最后家园”[1].侗族的生活背景决定了侗族文化全凭心传口授，顽强地世代相传，所以，研究侗族数学文化主要是研究侗语中所表达的数学概念和相关计算，以及他们生活中特有的鼓楼建筑、民居、民间工艺、服饰、刺绣等载体所蕴涵的数学知识.

2 侗族生活中的数学概念及相关计算

经过漫长的发展，侗族生活中也形成了“数”的抽象概念及相关运算.侗族母语中所表达的基数和序数与中国传统数学基本相符，最小的自然数是1；零没有确定的读法，仅用“无”或“完了”表达其意；分数概念较为清晰，也有小数的意义，但表达不了纯小数；没有负数、无理数等概念.有关数的运算，一般都与市场交易或生活的实际问题联系在一起，是典型的古代中华民族以问题解决为目的的数学观.以乘法运算为例，设单价为a，件数为x，求交易额时，相关的加减法及扩大（或缩小）10n倍的乘法运算与人们现在的理解完全一致，但2至9的乘法却没有“九九表”可用，而是充分利用2、及10的倍数进行运算[2].基本方法如下：求一个数的2倍，是通过计算相同的两个数的和去实现；求一个数的3倍是通过求这个数的2倍加上它的1倍的和去实现；求一个数的4倍，则是通过计算它的两个2倍的和去实现，或通过这个数的5倍减去它的1倍的差去实现；而求一个数的5倍，或是通过这个数的2倍的2倍再加上它的1倍的和，或是求它的10倍的一半去实现的；求一个数的6倍，则可以通过它的5倍加上它的1倍的和去实现；如此等等.母语中所表达的这些算法，可以总结归纳并“翻译”为下列函数：

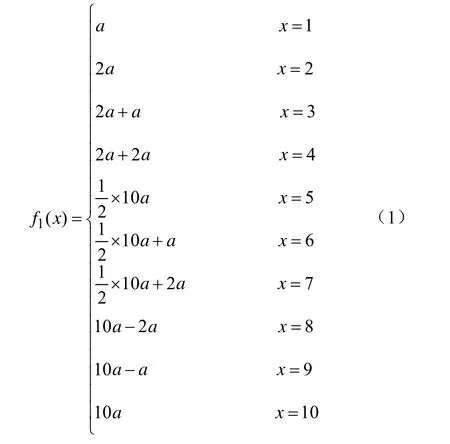
运算中，他们不拘一格，并不完全按（1）式计算，如，当x=5，6，7时，对应的乘法运算有时取：f(5)=2a+2a+a，f(6)=10a−2a−2a，f(7)=10a−2a−a等，但是，他们始终注意有效地利用2、及10的倍数去实现乘法运算.

在侗族的“乘法”运算中，无论是20以内的“乘法”，还是30以内的“乘法”，或是更大的数的“乘法”运算都能继续用分段函数表示.例如，用公式表示20以内的“乘法”运算等.

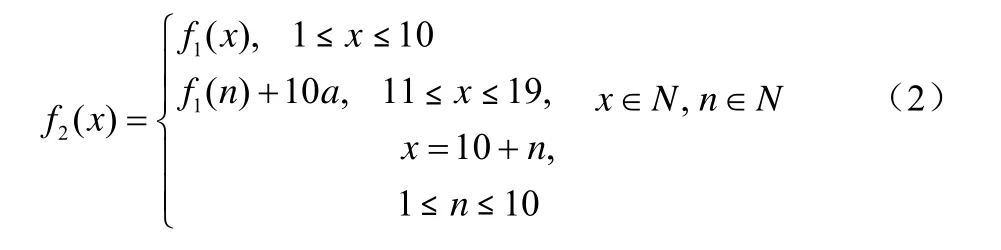
这样，古代侗族巧妙地实现了将乘法转化为加减法的运算，既克服了没有“九九表”的困难，又不陷入乘法意义中的连加运算.在义务教育基本普及的今天，仍然传承并使用上述方式进行运算的只有极少数老年文盲妇女.

几何概念较为丰富，如三角形、多边形、圆、直线、平面等在侗语中都有，但抽象程度不高，远未达到“数学化”的程度，由此容易带来概念上的含混不清，这种现象是尚未进入现代数学文明的中华民族语言的共同特征.

由于侗族没有文字，所以没有任何数学符号，数学概念、公式与运算方法全凭口传心授世代相传.

3 以鼓楼为载体的侗族数学文化

侗族聚居的村寨都有鼓楼，鼓楼是侗族所特有而其他民族所没有的建筑，是侗族全部精神性的文化结晶，是最具有象征性的文化符号[3].鼓楼雄伟、壮观，占地面积百余平方米，高数十米不等.如此高大的建筑，其整体以杉木做柱、枋，凿榫衔接，横穿斜套，纵横交错，结构严谨牢固，却不用一钉一铆，其中蕴涵着丰富的数学文化，也体现了侗族祖先的数学应用与思维特征.

鼓楼主体结构对称和谐，其平面图通常是正方形，正六边形和正八边形，常见的八角鼓楼平面图通常由正方形和正八边形复合组成.如：从江县增冲鼓楼平面结构图内部是一个正方形，而外部是一个与正方形同心的正八边形组成等.所以，建筑师在建造鼓楼时大量地涉及与正多边形相关的计算.

3.1 与正八边形相关的计算

八角鼓楼的建造，涉及正八边形的边长a与半径R的计算.在今天可用公式a=2Rsin22.5°表示.显然，22.5°不是特殊角，计算结果无疑是取其近似值.但古代侗族对角度的概念并不十分清晰，对此，他们有自己的计算方法：

图2是八角鼓楼楼冠（如图1）在平面上的正射影，已知正八边形半径OMi（OMi=ONi，i=1,2,3）的长度，则边长MiNi的确定是通过公式

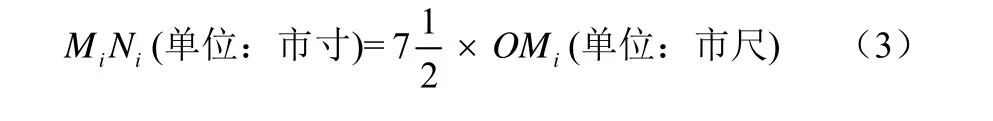
来实现（计算说明：例如，OMi=4市尺，代入（3）式，得MiNi=30市寸，即MiNi=3市尺）.古代侗族没有系统的三角函数知识，加上侗族语言难以表达纯小数的读法，他们巧妙地运用了10进制单位进行换算来实现公式（3）的计算.它显然是一个较好的近似计算，这是侗族鼓楼建筑师在长期的实践中总结得到的结果.

值得注意的是，八角鼓楼楼冠的屋面需要制作如图3的三角架，其中OBi（i=1,2,3,…）的长度为已知，角O的大小与AiBi长度的确定一般也是通过公式

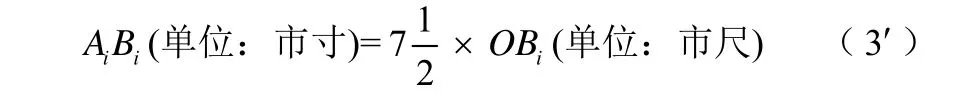
来实现.

由此可见，侗族在三角形概念的分类中不是十分清晰，他们知道直角三角形与其它类三角形的区别，但在相关计算时，有时又容易出现这种含混不清的处理方式.因此，在侗族地区实施数学教育时应高度重视这个问题.

图1 八角鼓楼楼冠

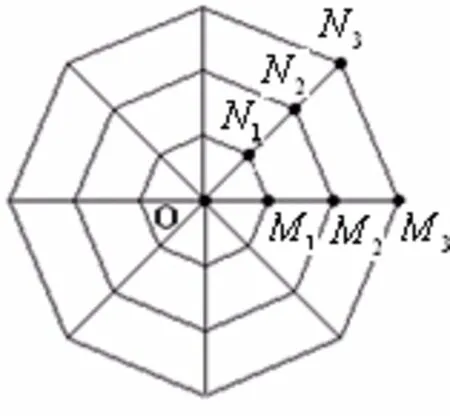
图2 八角鼓楼楼冠正射影

不过，没有文字的侗族，为了减轻鼓楼建筑师记忆的负担，也便于建筑工人的操作，在楼冠的屋面三角架（图3）的制作中他们类比公式（3）得到公式（3′）来实现这个计算，不失为明智之举.

有意思的是，上述侗族鼓楼建筑师在直角三角形“已知邻边求对边”的问题上，类比正八边形的“已知半径求边长”的公式，得到图3中直角三角形OAiBi的三边恰巧是“勾3、股4、弦5”的关系.

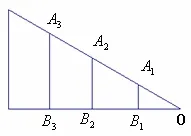
图3 三脚架

在复合型八角鼓楼中，通常第一、二层是四面倒水，从第三层起变为八面倒水，建造时还涉及如图4的相关计算，即若正方形边长AB=1，则图4中较大（与最外层正方形相接）的正八边形的边长A1E是多少？点A1应在对角线OA上的什么位置？A2呢？第二个正方形的边长是多少？等等.

当然，与八角鼓楼相关的计算还有很多，如有关角度的处理，等等，在此不再赘述.

3.2 与正六边形相关的计算

建造六角鼓楼，需要制作正六边形.进一步调查发现，黎平县境内有部分鼓楼建筑师用“九五分六角”的方法去近似地6“等分”圆周，这是古代侗族对角度概念尚未完全掌握的历史条件下6等分圆周的近似方法.即制作一个对边为9市寸（市尺、市寸是侗族至今仍然普遍使用的长度单位），邻边为5市寸的直角三角板（如图5），在这个直角三角板中，较大的一个锐角约为6055′° （接近60°），用这个较大的锐角当作60°角去“等分”圆周，得到正六边形，以实现6角鼓楼的建造.6“等分”圆周具体过程如下：

（1）在圆柱形（实际上是不规则的）木料的一个底面（如图6）上作线段PQ及中点O，用如图5的三角板ABC中的点A与点O重合，AC边与OQ边重合，AB与底面圆周交于点M，连接OM，得到∠MOQ≈6055′° .

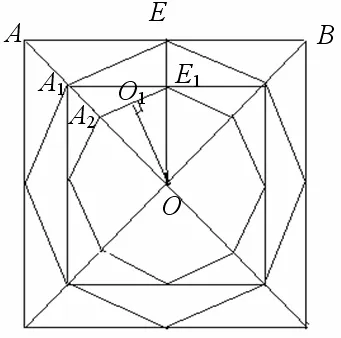
图4 相关计算

（2）作OM的反向延长线与底面圆周交于点N，得到∠NOP=∠MOQ.

（3）用三角板ABC中的点A与点O重合，AC边与OQ重合，AB与底面圆周交于另一点R，再用三角板ABC中的点A与点O重合，AC边与ON重合，AB与底面圆周交于点S，在RS弧上找到中点T，连接OT.

（4）作OT的反向延长线与底面圆周交于点W（如图6所示）.

就这样，实现了6“等分”圆周的目的，每个角的误差都不超过55′.

有时候他们干脆将上述的步骤（3）及（4）简化为：

（3′）如图6，用三角板ABC中的点A与点O重合，AC边与OQ重合，AB与底面圆周交于另一点R，连接OR，再作OR的反向延长线与底面圆周交于点D，以此实现6“等分”圆周.但这样做∠NOR和∠MOD的误差较大，接近150′° .

以上说明，古代侗族在不完全掌握角度概念的情况下，通过长期的实践总结出了这种独特的“九五分六角”的近似计算方法，实现了6“等分”圆周的目的.同时也说明古代侗族早已掌握了“对顶角相等”这条古老的命题的应用.

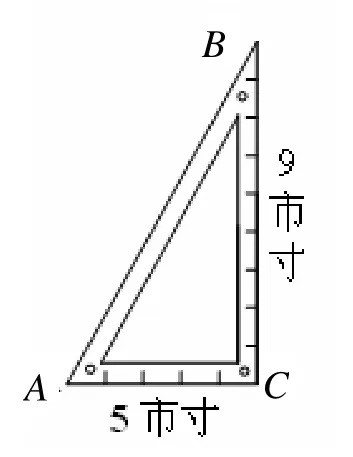
图5 三角板

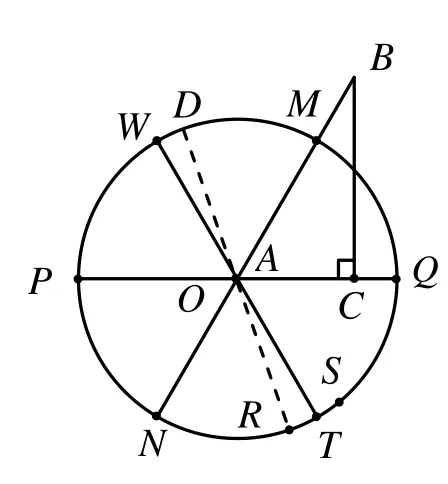
图6 辅助线

3.3 鼓楼中的近似计算

在鼓楼建筑中，无论是四角鼓楼、六角鼓楼或是八角鼓楼，近似计算都是无法回避的事实.例如，上述用“九五分六角”的方法得到正六边形，就属于近似计算问题.还有，运用公式（3）计算正八边形的边长就是一个取边长的不足近似值的近似计算，误差不超过0.015 5，这在半径不超过3 m的楼冠上误差不到4.65 cm；鼓楼建筑师处理这样的误差问题全凭长期的做工经验，并根据柱头的大小、正八边形半径的长短来估计误差大小，进而去弥补不足近似值，同时还利用杉木的忍性在连接两个柱头的木枋上做成如图7这样的两个“鱼尾”弥补其不足，同时“鱼尾”又起到了掩盖柱眼以增强建筑的美感和固定柱子位置的作用.真可谓是巧夺天工.

图7 鱼尾

在鼓楼建筑中还经常遇到求正方形对角线长的问题.鼓楼建筑师通常采用的计算方法是：

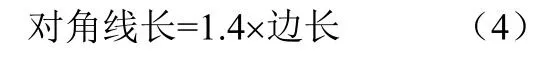
侗族生活中没有无理数的概念，但以上说明他们如同其他民族或地区的文明一样利用了有理数做近似计算，而且无论是四角鼓楼、六角鼓楼或是八角鼓楼，在相关的长度计算中一般都取不足近似值，不足部分留给两个“鱼尾”去弥补，这是侗族鼓楼建筑中近似计算的基本特征.

3.4 鼓楼中的黄金分割

美的建筑一般都与黄金分割比例相关，鼓楼也不例外.

带着问题，项目组对鼓楼的各部分结构进行了专门的测量，发现有为数不少的鼓楼在结构上十分接近黄金分割比例，内部结构中的主承柱、檐柱、瓜柱分拉枋的分点也都十分接近黄金分割点.

例如，从江县增冲鼓楼高25 m，内有4根主承柱，高15 m.该鼓楼由楼体、楼颈和楼冠3部分构成，从远处眺望似人体一般形状，以楼颈为分点其楼体高（即为主承柱高度）15 m与楼高25 m之比是0.60，十分接近黄金分割比例，这恰似咽喉是人体结构中的一个黄金分割点一样[4]，鼓楼楼颈是其黄金分割点.

再如，图8是从江县的则里鼓楼平面图[3]，A和D为檐柱，B和C为主承柱，其中AB=CD=265cm ，BC=410cm ，由此，BC≈0.6074AC=0.6074BD，即点B（或点C）接近线段AC（或线段BD）的黄金分割点.

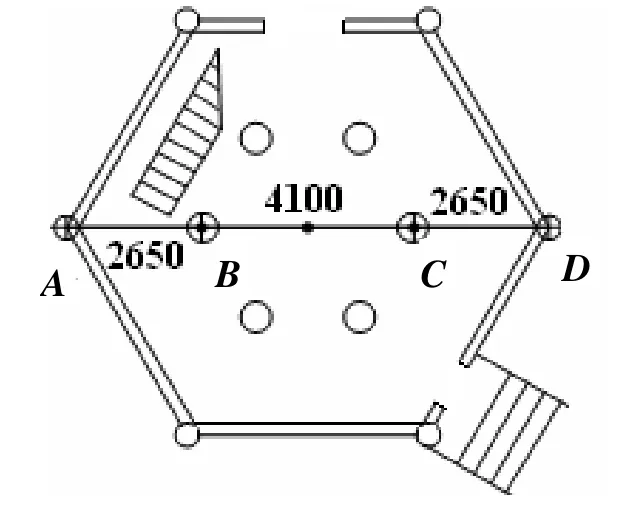
图8 则里鼓楼平面图

还有，图9为从江县小黄鼓楼的一排翘檐的结构图，经测量，A1A2=107cm，A2A3=57cm，A3A4=B2B3=65cm，A4A5=173cm，B1B2=95cm，B3B4=48cm，B4B5=125cm ；由此，A1A2≈0.6524A1A3，点A2较接近线段A1A3的黄金分割点；A3A5≈0.5920A1A5，点A3更接近线段A1A5的黄金分割点.而B1B2≈0.5938B1B3，点B2与线段B1B3的黄金分割点的误差较之更小；B1B4≈0.6246B1B5，点B4接近线段B1B5的黄金分割点的程度更好.

此外，对其它鼓楼的翘檐等结构的实地测量，如黎平县纪堂鼓楼等，也得到类似的结果.

黄金分割比例的应用，不仅仅是鼓楼造型美的需要，它还蕴涵着丰富的力学原理.对此，侗族鼓楼建筑师没有做任何解释，面对着这些百年以上的鼓楼，我们只能说这些人类早期文明的数学文化以鼓楼为载体通过侗族建筑师心传口授传承至今.

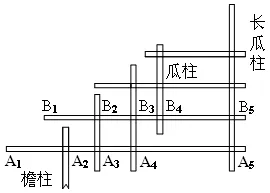
图9 小黄鼓楼的一排翘檐的结构图

4 等差数列求和公式在侗族生活中的应用

侗族长期过着自给自足的生活，男耕女织千年不变.图10是侗族家庭中常用的织布机.图11是图10中卷布筒的横截面示意图.

调查发现，侗族妇女织布时通常能够根据图11中半径OB的大小估算出布匹的长度.例如，要织一匹长度为18m的布匹（不妨设布的厚度为0.1cm，卷布筒的半径OA=3cm），她们只需要看这卷布的外圈半径OB的大小约为8m就知道布匹长度基本达到要求.这是长期的实践经验告诉她们如何通过半径OB的大小估算其布匹的相应长度，其实她们的“估算”可作如下解读：

依题意，假设绕在卷布筒上的第n圈的半径为an，显然，a1，a2，…，an，…，构成一个等差数列，其中a1=3+0.1，公差d=0.1；又设布匹的总长度为Sn，取b1=2π×3.05，由等差数列求和公式知：

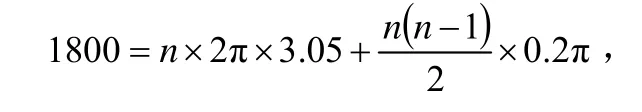
即n=51；此时布筒的外圈半径约为：

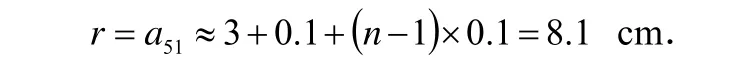
本例与现行高中教材“铜片绕在圆盘上”的问题类似，它显然是高中教材的一个补充和拓展.

图10 侗族织布机

图11 织布机卷布筒的横截面

侗族鼓楼建筑师在鼓楼的建造过程中，也经常用到等差数列知识去计算相关的问题使做工达到分毫不差的程度.图12是鼓楼楼冠侧面装饰图[5]，共有4个侧面，每个侧面的装饰图案自下而上、从左到右按一定的规律排列.图中每3个直角扇形为一组，每相邻的两个侧面的两组共由5个直角扇形构成（其中位于侧棱上的直角扇形为两组公共的扇形）.图中的每个侧面自下而上从第一层到第五层依次为6、7、8、9、10组，分别有18、21、24、27、30个直角扇形，而4个侧面的第一层到第五层的直角扇形依次是68、80、92、104、116个，4个侧面总共需要460个直角扇形.而且每一组直角扇形的中间一个都与另两个不同，即中间一个为图13中的阴影部分OPQ（为了叙述的方便我们也称它为直角扇形），另两个才是真正的直角扇形.形如图13的这种直角扇形共有160个，真正的直角扇形为300个.对如此繁杂的数据，鼓楼建筑师能在施工前准确无误地计算出来，他们是用等差数列及其求和公式实现的，尽管他们因没有文字而无法表达其计算公式，调查中，发现他们大多应用公式

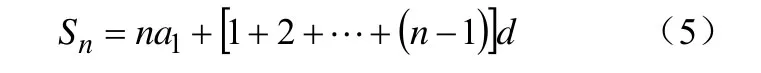
进行等差数列求和的运算.

图12 鼓楼楼冠侧面装饰

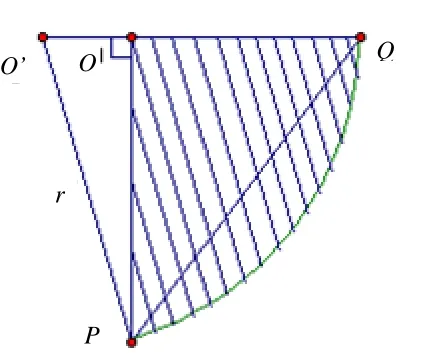
图13 直角扇形

类似地，六角和八角鼓楼楼冠侧面装饰图的直角扇形的数目更大，他们同样能够运用等差数列求和公式进行计算.

还有，鼓楼自下而上每层的正八边形的半径也呈等差数列[6].

5 侗族生活中的平面镶嵌

在侗族地区不仅仅保留侗族所特有而其他民族所没有的鼓楼，也保存着农耕文明时期的侗族民居，是中华本土建筑文化的“活化石”，同时，还传承着丰富的竹编等传统工艺，难能可贵的是这些建筑和传统工艺中蕴涵着丰富的数学文化.

图14是侗族地区常见的竹编，显然，图中是由边长相等的正三角形和正六边形两种图形镶嵌成的一个平面.

图15是侗族民居窗户的花格，显然，它也是由正三角形和正六边形两种图形镶嵌成的一个平面，所不同的是，此时的正三角形边长是正六边形边长的两倍.这为研究者研究当正三角形的边长是正六边形边长的n倍时能镶嵌成一个平面（图16）提供了现实模型.

在侗族的传统工艺中，如上所述的窗户花格，还有服饰中的图案等都有丰富的镶嵌问题.而且正三角形、正四边形、正六边形，以及正三角形与正四边形、正三角形与正六边形镶嵌成一个平面的模型都有.

图14 侗族地区竹编

图15 侗族民居窗户花格

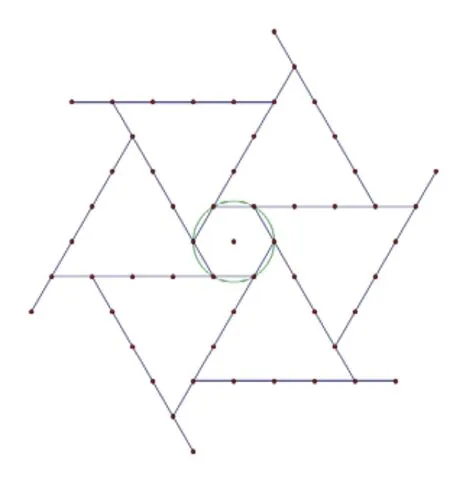
图16 平面镶嵌模型

6 侗族服饰中的数学文化

侗族女性的服饰千姿百态，或款式不同，或装饰部位不同，或图案和工艺不同，或色彩和发型、头帕不同.服饰注重审美，朴素与华贵相得益彰，充分展示出侗族女子的聪慧和高超技艺，是民族文化之瑰宝.

常见的侗族织锦，其图案分布规律性强，由大小相等的菱形依次相接排列而成，每个菱形内都有1朵花，每一朵花又由8个菱形的花瓣构成（如图17a），两个菱形之间的上下空白处分别绣有4个花瓣（如图17b）.按照规律，作出图17c，如果需要，还可以继续作出相关的图形.这除了是一个等差数列问题，还与平移变换、对称等数学知识相关.

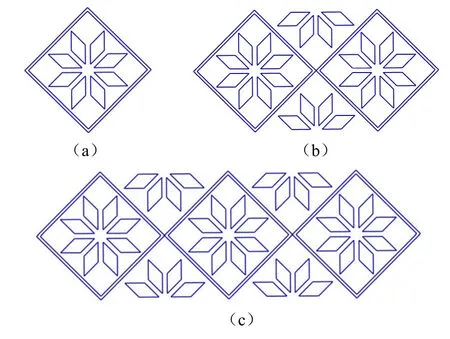
图17 侗族织锦

再看图18，这是侗族女孩子经常穿戴的围腰，图形自上而下，围腰外围和里面的图案都有很多条弧线，图案优美、和谐大方.这里无疑蕴涵着丰富的数学文化，恕不一一列举.

图18 侗族女孩子穿戴的围腰

侗族服饰、刺绣，特别是挑花、数纱绣等工艺与图形的全等（包括图案的对称平移）、面积的大小和图案各线段的长短都有关系，它有着丰富的数学文化内涵.在民族地区实施数学教育，若能注意参考这些民族文化，创设必要的数学情境，对提高少数民族女童对数学的认识和理解，其效果不言而喻.

7 “二分法”是侗族常用的数学方法

“二分法”是基本的数学方法，是新一轮数学课程改革中新增加的教学内容.其实，在侗族数学活动中早就有“二分法”的应用.

如前所述，侗族生活中的乘法运算公式（1）就有效地运用了2和的倍数将乘法转化为加减法的运算，这里充分体现了“二分法”在乘法运算中的应用.

“二分法”在侗族的生活实践中也有着广泛的应用.

图19是古代侗族传承下来的碾米房的水轮车.该水轮车依靠水的冲力使其转动，形成动能，并通过轴心的立柱带动上一层石巢轨道的石轮转动，以实现碾米功能.这个水轮车主要由两个同心圆和连接同心圆的木板和木枋构成，这本身就蕴涵着丰富的数学和力学原理.制作时，首先运用前述“九五分六角”的方法获得6个圆心角约为60°的“全等”扇环，然后分别在每个扇环中插入1片叶片，将扇环分为两个全等的扇环，用同样的方法依次将扇环“一分为二”，使每个圆心角为60°的“全等”扇环插入7片叶片，在圆弧上实现了水轮车叶片的加密.克服了在对角度概念还不清晰的情况下n等分圆弧带来的困难.

图19 碾米房的水轮车

研究者还注意到，如前所述，鼓楼楼冠的屋面需要制作如图3的三角架，AiBi长度的确定一般也是通过公式（3′）来实现的.而鼓楼楼冠以下的各层翘檐也要制作如图3的三角架，角O的大小与长度的确定是将公式（3′）中的7i改为5而实现（如图20）：

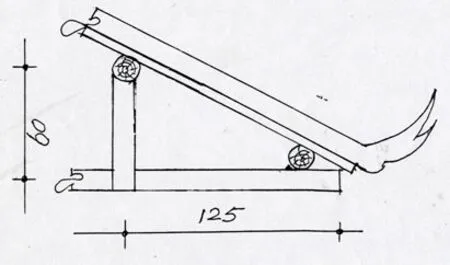
图20 鼓楼楼冠以下的翘檐测量

AiBi(单位：市寸)=5×OBi(单位：市尺) （3′′）即，直角三角形的“对边是邻边的一半”.

需要说明的是，图20是对鼓楼楼冠以下的翘檐测量的结果，单位是cm，而侗族所用的工具是市尺，且侗族测量或计算到市寸以后的数字通常忽略不计，所以，数据有误差.但如果转换为市尺并按照侗族的这一习惯的方式进行测量和计算，那么125 cm=3.75市尺，其中第二位小数中的5是市寸以后的数字忽略不计，他们只记为3.7市尺，将OBi=3.7市尺代入公式（3′′）得到AiBi=18.5市寸，而这里第一位小数中的5是市寸以后的数字又忽略不计，故取18市寸（即60 cm），这正好是测量的结果[3].

侗族民居中的屋面三角架一般也是应用公式（3′′）制作成为“对边是邻边的一半”的直角三角形.这让研究者再一次地看到了“二分法”这一基本的数学方法在侗族生活中的广泛应用.