中日三角比内容比较——以上海教育出版社和数研出版社出版的教科书为例

陈月兰

（华东师范大学 数学系，上海 200241）

1 引 言

“三角比”这个知识无论在中国还是在国外都是非常重要的数学内容，它是连接代数与几何的重要纽带之一.中国和日本同处于亚洲，由于受中国文化特别是儒家思想的影响，日本在对待教育、思考问题等方式上与中国有很多相似的地方，比如重视教育、注重基础等.然而随着时代的变迁，西方教育理念的引入，日本在一些观念上也发生了变化，这些差异同样反映在数学教科书编写与内容处理方式上.这里将以日本数研出版社（岡部恒治主编）等出版的《高等学校数学I》[1]（2011）（以下简称教研社教科书）和上海教育出版社出版的《数学》（2007）（以下简称上海教科书）为原始材料，选取“三角比”内容，进行深入细致的比较研究，详见表1.

表1 基本信息

2 研究问题

主要围绕3个问题展开，首先，中日两国关于三角比主要内容和顺序上有何特征；其次，知识点的呈现方式；最后，三角比概念核心定理——正余弦定理在构建上有何特征，进行深入研究.

3 研究方法与结果

关于教科书比较的研究方法的文献有很多，既有宏观的又有微观的，既有本国教科书之间的比较（Mesa（2010））[4]，又有国际（Stevenson和Bartsch（1992））[5]或跨文化的研究（Li（2000），Son（2005）[6～7]，Charalambous et al.（2010））.根据这里的研究问题，将借鉴Charalambous et al.（2010）[8]的研究方法，构建宏观与微观的研究框架，宏观层面主要从教学目标、内容顺序两个视角展开；微观层面将从知识呈现、三角比概念核心定理的构建两个视角进行比较.

3.1 宏观层面

3.1.1 主要内容及顺序

打开上海与数研社教科书，可以发现教科书的编写风格比较接近：简洁，结构紧凑.比如上海教科书编写格调基本上是：引言—引入概念或定理—例题—练习—本章小结；数研社教科书是：引起关注—导入—概念或定理—例（或例题或应用例题）—练习（注意）—补充习题—章末习题A—章末习题B.

上海与数研社教科书的差异也是显而易见的，首先是整个高中数学教科书的册数不同：上海数学高中教科书分为高中一年级第一学期、第二学期，高中二年级第一学期、第二学期，高中三年级，高中三年级理科拓展、高中三年级文科拓展，共计7册；数研社教科书是数学I，数学II，数学III；数学A，数学B，数学活用，共6册.尺寸大小差异，上海教科书是大开本A4（16 k，297 mm * 210 mm）尺寸，数研社教科书是A5（32 k，210 mm * 148 mm）尺寸，大约只有上海的一半；其次是内部，比如同样是例题，数研社分为例、例题和应用例题3类.“例”在解答题目时带有说明，重点部分会用颜色标出；而“例题”则没有这些，有的是明显的“解答”字样，为学生解答做示范；“应用例题”除了有解答，还列出了思考方法.这说明日本是非常注重细节的，安排的例题用意也是不一样的.

这里所指的主要内容是指“三角比”章节中出现章节名、单元名、黑体字.上海教科书初中“锐角三角比”主要有比值、名称（正弦、余弦、正切和余切）、锐角三角比定义、特殊角的三角比、一般角的三角比、计算器）求锐角的三角比的值、解直角三角形、解直角三角形的应用.高中主要有：任意角的度量（包括2kπ+α）→弧度制→任意角的三角比（正弦，余弦和正切）→同角三角比关系→诱导公式（-α，π+α，π-α）→两角和与差的余弦、正弦和正切→二倍角与半角的正弦、余弦和正切→正弦定理→余弦定理→应用（解斜三角形，测量）.

日本锐角三角比的主要内容有比值、名称、三角比定义、解直角三角形、特殊角的三角比、一般角的三角比、查表）→同角三角比的关系→诱导公式（90°-α）→三角比概念扩充到钝角（0°≤α≤180°，正弦，余弦和正切）→诱导公式（180°-α）→同角三角比的关系→特殊角：0°,30°,……，180°的三角比→正弦定理→余弦定理→定理应用→三角形面积（正弦与三角形面积、多边形面积、三角形的内切圆与面积、海伦公式）→在立体几何中的应用（利用定理测量实际立体问题，利用定理求体积、二面角的平面角等）.

比较分析：从上面列出的主要知识点和顺序可以发现，两国教材主要内容相似，高中三角比基本上都是沿着任意角的三角比→同角三角比的关系→诱导公式→正弦定理→余弦定理→应用这条路线走的.但在细小处理上有差异.比如上海教科书从锐角一下子扩充到任意角，角度制与弧度制混合使用，后者为主；日本在同角三角比关系与诱导公式之间有一次小的迂回；多了一个环节——钝角，即按照锐角→钝角→任意角这样的小步制扩充方法进行，仍然是角度制.从角扩充的跨度到弧度制的采用，折射出上海教科书步子大、内容相对集中，体现了一定系统性的同时，也暴露出与其它知识联系不够紧密的弱点；数研社教科书显得比较保守，步子小、铺垫到位，求一般角的三角比时拒绝计算器而是采用传统的三角比表.应用范围广，从求三角形面积、测量三角形边或角、三角形内切圆与面积、多边形面积、求体积、求二面角的平面角、空间图形的边角关系等.在应用过程中为学生编织了一个知识网，这和他们在教学目标（高等学校学习指导要领2009）[9]中所提倡的理念，即通过数学活动、通过应用感受数学的好处相吻合.

结论：两国主要内容相似都强调概念的理解、关注基础，体现了中日的共性.但在角的扩充速度上、对一般角的处理上以及应用上存在差异.

3.2 微观层面

3.2.1 呈现方式

如同前面所述，“三角比”是基础数学中一个非常重要的内容，因此相关的具体知识点有哪些异同？又是如何呈现的是一个值得探讨的问题，为此对上海教科书与数研社教科书进行了一番梳理，其结果如表2所示.

比较分析：从表2中可以清晰地看到，两种教材都把这部分内容定义为“三角比”（注意有的国家或地区称为锐角三角函数），主要知识点上接近均有锐角三角比概念、钝角三角比概念、同角三角比关系、90°、180°的诱导公式、正弦定理、余弦定理、应用以及测量等两国都有，且都被安排在必修中；但在时间安排、知识应用、角度度量和一般角的处理方式上显示了差异：

（1）内容与学段.上海教科书把三角比这部分知识分成“锐角三角比”与“任意角三角比”两大块处理.前者被安排在初中（9年级第一学期），后者被安排在高中（10年级第二学期），这说明了上海数学课程体系正在由原来的直线型向螺旋式发展；日本虽也是分阶段完成的，高一学三角比主要涉及锐角和钝角，高二学“三角函数”，内容有任意角、两角和、倍角、半角的正弦余弦等.另外，日本学者认为“比”这个概念与除法、函数概念有很强的内在联系，是数学中的难点和重点，因此他们将通过小学渗透（Masami Isoda（2000）），初中正式引入，高中正规学习三角比、函数等3个阶段完成.

表2 中日教科书三角比相关知识点对比

（2）角度单位.上海教科书初中“锐角三角比”中角度的度量均使用角度制，但一到高中马上引入了弧度制，紧接着是任意角的概念；角的度量采用的是角度制与弧度制混用方法，角度制较少，除了P40、P41、P49、P56、P58上各有一题外，其余均为弧度制.由于任意角的概念日本要在高二的“三角函数”中才正式引入，因此在三角比这一章没有涉及弧度制，全部采用角度制表示，因此显得比较简单不易混淆.

（3）对一般角的三角比处理方式上.上海初中“锐角三角比”部分，利用计算器来处理，比如P69上的例题2，高中则没有涉及一般角.在数研社教科书上一般角是采用传统的三角比表P123（见图1）和附录来处理的.从这个差异可以看出日本虽然在计算器领域比较先进，拥有像“卡西欧”这样的品牌，但他们在学校教育，特别是基础教育阶段为保证学生的计算能力不轻易采用计算器或计算机.

结论：中日两国在“三角比”相关知识点的选取上大体相同，但在时间安排、知识应用、角的度量方式以及对一般角的处理方式上表现出了差异.虽然三角比的内容上海要多于日本，但花费的课时数要少于日本，上海初高中课时数合计24节，共960分钟；日本27（25～30）课时，看上去只多3节，但由于日本每节课是50分钟，比中国（40分钟）足足多了390分钟，即实际比上海多了9课时，可见日本在主要内容上舍得花时间.

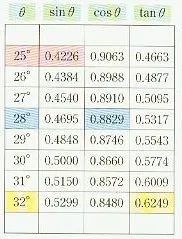
图1 传统的三角比表

3.2.2 三角比概念构建方式

关于三角比概念是用直角三角形好还是利用单位圆好，这在国际上是有争论的，有的赞成用直角三角（Ellis, J.（1990））（Lloyd, D.G.H.B.（1976））、有的认为用单位圆好（Ince, L., & Johnston, A.（1988））（Shear, J.（1985）），还有认为两者结合为佳（Ellery, P.（1980））（Satty, G J.（1976）），那么上海教科书与数研社教科书采用哪种方法呢？通过比较发现，上海在初中阶段通过有公共锐角的直角三角形相似（3个画在同一个图中）得到相似比，从而得出给定直角三角形的锐角则比值是一个定数的结论；然后通过一个问题“当直角三角形中一个锐角的大小变化时，这个锐角的对边与邻边的长度的比值随着变化吗”的解答，说明该比值随着锐角大小的变化而变化，最后点出关键：在一个直角三角形中当锐角A的大小确定后，不论该直角三角形的边长如何变化，∠A的对边与邻边的比值总是确定的，称为该角的正切（tantA）.然后依次给出cotA、sinA和cosA概念，从而引出三角比概念.高中则利用单位圆把三角比概念扩充到任意角（见图2）.

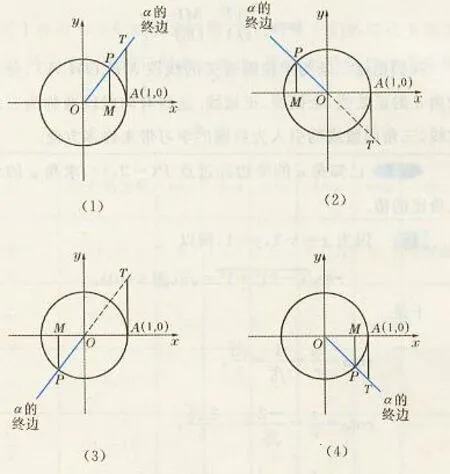
图2 上海教科书任意角三角比概念

日本最初锐角三角比的概念也是通过直角三角形引出的，首先给出两个含有30°角的直角三角形，一大一小用两个图表示，得出相似比和具体比值，然后点出这些比值与三角形的大小无关，总是一个定植.继而再用一个一般的直角三角形，设锐角为θ，斜边为r，θ的对边为y，邻边为x，再一次指出y/r，x/r，y/x的各值与三角形的大小无关，仅由角θ的大小决定，这些分别称为正弦、余弦和正切，再引入符号，最后点出这些统称为三角比.钝角三角比概念则是利用半圆加直角三角形（见图3）将锐角三角比概念扩充到钝角.他的特色是通过钝角、通过半圆过渡，比较仔细，这为后面任意角的扩充奠定了基础扫除了障碍.

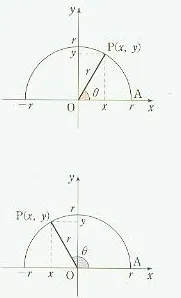
图3 数研教科书任意角三角比概念

比较分析：上海与日本均采用直角三角形与单位圆两者相结合的方式.差异在利用直角三角形相似时，上海是将3个直角三角形放在一个图形中，强调的是“在一个直角三角形中当锐角θ的大小确定后，不论该直角三角形的边长如何变化，∠θ的对边与邻边的比值总是确定的”；日本虽然也是用直角三角形相似引出比值，但他们给出的两个直角三角形都是含有30°角的特殊三角形，而且分别画在两个图中，两个三角形大小明显不同.然后是一般的直角三角形，边的名称也变得抽象，分别用x、y、r表示，强调的是y/r，x/r，y/x的各值与三角形的大小无关，仅由角θ的大小决定.

从两个图形（上海是一个图形）、特殊直角三角形（上海是一般直角三角形）、比值由锐角决定而与三角形的大小无关（上海的提法：一旦锐角确定，无论直角三角形的边长如何变化，比值为定值）等细节中可以发现日本与上海的差异.日本在图形表达和语言阐述上比较细腻，教科书编写走的是一条从具体到一般的路线，强调学生的可接受度.同样的内容日本是在高中教科书，中国在初中，因此难度上要高于日本.

结论：上海教科书与数研社教科书均采用直角三角形与单位圆兼并的方法引入三角比概念，不同的是在具体引入锐角三角比概念的方式上数研社教科书无论是在图形的展示还是举例方面比较具体、简单容易接受.

3.2.3 核心定理——正弦定理与余弦定理的构建与证明方式比较

在三角比中有两个重要定理，分别是正弦定理与余弦定理，下面将分别对他们进行比较.

正弦定理

图4 正弦定理上海教科书推导过程

数研社教科书则通过探讨三角形外接圆直径与某个角的正弦值关系，运用分类讨论思想将内接三角形分为锐角、直角和钝角3种情况处理，均得到a=2RsinA，即=2R（P138）见图5—7，涉及到的知识点是平几中圆周角与同弧所对的圆心角关系，同理可以得到=2R，=2R.从而得到正弦定理：

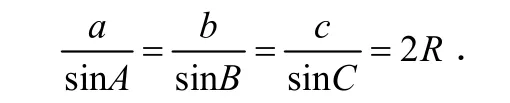
图5 正弦定理数研教科书推导过程1

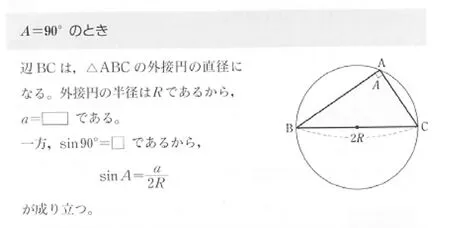
图6 正弦定理数研社教科书推导过程2

余弦定理

上海教科书通过求两点间的距离推导出余弦定理.主要步骤：

（1）建立坐标：把一个斜三角形放在坐标系中；

（2）利用三角比确定三角形的3个顶点的坐标；

（3）两点间的距离公式.

数研社教科书则通过勾股定理导出.主要步骤：

（1）过三角形某一定点作对边的高，构建直角三角形；

（2）正弦、余弦三角比表示某两条边；

（3）利用勾股定理求出边之间的关系.由于过某一顶点作高可能在形外，也可能在形内，所以需分类讨论，但不管哪一种情况都能得到余弦定理.

比较分析：对于三角比中的核心定理正弦定理，两国都运用了基本知识——三角比；相异处上海强调数形结合利用解析几何解决问题，但未得到定值，定值是通过一个例题加以说明的；日本则注重三角比与平面几何的联系，不仅得到比值同时得到定值2R.后者的推导方法学生容易理解和记住定值2R，而通过例题的方式导出则不易引起学生的关注，毕竟定理与例题的地位不同.同样余弦定理也用到了三角比概念，在具体方法上上海教科书偏向代数法，数研教科书偏向几何.究其原因主要与其背后的教科书体系有关：在上海教科书中，平面几何内容全部放在了初中，高中几乎不涉及，因此采用代数方法也是情理之中.日本平面几何内容分散在初中和高中，初中主要涉及三角形全等、相似、圆的性质（一部分）等，高中主要是研究三角形的几个心、圆中的相交弦定理、圆与内接四边形、两圆位置关系等.因此此时日本用平面几何知识来推导余弦定理则很自然.到底用代数法好还是几何法好，在此不能妄加评论，但有一点是肯定的，从学生角度出发，哪种方法符合学生的认知或容易被接受理解哪个就是最好的.

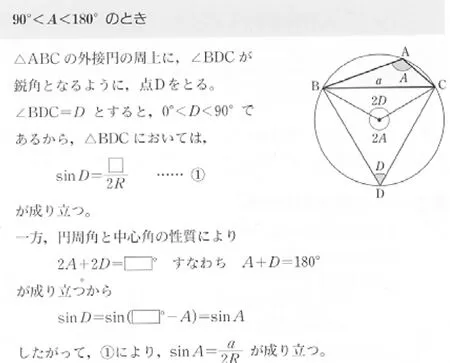
图7 正弦定理数研社教科书推导过程3

结论：（1）虽然数研社教科书没有把任意角纳入三角比中，但钝角三角比的定义方式与上海教科书任意角的三角比的方式基本一致，前者利用半圆、后者利用整个圆.（2）两国正弦定理的内涵不尽相同，上海是日本则为=2R.（3）在正弦与余弦定理的推导上，上海偏向代数法，日本则偏向几何法，这反映出背后的不同课程体系，这将在讨论中详细阐述.

4 讨 论

上海教科书和数研社教科书在“三角”这块知识的前期都使用“三角比”这个专用术语，可见两国都非常重视“比”的概念，要知道不是所有的国家和地区都是如此的.比如中国人民教育出版社出版的教科书数学①（2004）[10]上称为“锐角三角函数”和“三角函数”.从上面的比较可以看到中日两国数学教科书的逻辑性强，条理清晰，没有过多地解释，教科书结构紧凑.注重基础、铺垫到位、强调知识结构的完整等，这些都反映了中日数学的共性.与此同时也明显看到两国在“三角比”细节上的诸多差异，产生这些差异的根本原因可归结为以下两点：

其一是理念上的差异，日本在经济上虽然属于发达国家，然而与西方国家如美国相比是一个非常保守的国家，特别在教育方面尤为突出，从日本教科书中至今还保留平方根表、三角比表、BASIC语言等都印证了这一点.明白了这一点就不难理解日本为什么在中小学课堂上不积极使用计算器、计算机等现代技术了.日本除了上一轮（每10年大约一轮基本）1998年的数学课程改革幅度比较大（有些异常）以外，一般都非常谨慎，无论是一个知识点还是数学符号的引入都慎之又慎，要经过反复推敲、多次讨论、权衡利弊后才作出最后决定，这些现象其实与日本民族有较强怀旧意识、拘泥细节强调完美有非常大的关系.与此相比虽然中国在经济上不是发达国家，但中国处在改革开放的时代，特别像上海是一个易吸纳新思想、接受新事物的城市，上海进行二期课改之时正好遇上美国、英国等试图建立全国数学课程标准、日本学习指导要领修订时期，从新课标中“学段”、“理念”等这些新名称的使用不难看出受国外的影响之深、之快.然而西方的是否都是好的？中国前面的改革（一期课改）是否都是失败的？如果不做研究不重视自己的特色，一切照搬外国的，这样是否会丢失和铲除中国教师长期积累起来的丰富经验和良好的根基？重新认识自我，对一期课改的结果进行深入仔细的评估，与此同时客观看待国外课标和教科书，深入科学地研究则势在必行.

其二，日本初等教育数学课程体系呈现给读者的是螺旋式上升，注重知识网络的构建，遵循着由下至上的一条路线，即初中数学教科书如何与高中衔接，高中如何与大学衔接.由于日本低出生率现象的持续，很多年前大学毛入学率就接近100%（名牌大学除外），为了使大多数高中生进入大学后能快速适应大学的学习，在若干年前就已开始规划高中数学课程体系在内容安排上如何由下至上.因此打开日本高中数学教科书，你会发现“离散和连续”内容是并存的，比如函数极限、微积分、以及概率的研究部分“连续型概率变量的期望值与方差”都说明了这一点.目前中国的教科书结构也正在向螺旋式发展，但下面教科书如何与上面衔接做得还远远不够，上海教科书至今没有纳入微积分就是一个具体的例子.然而随着中国大学扩招的继续，出生率的降低，上海也即将面临日本的情况，未雨绸缪，也应该从现在起进行这方面的研究、规划并采取相应的措施.

[1]岡部恒治.高等学校 数学I [M].东京：数研出版社，2011.

[2]邱万作.数学 九年级第一学期（使用本）[M].上海：上海教育出版社，2007.

[3]袁震东.数学 高中一年级第二学期（试用本）[M].上海：上海教育出版社，2007.

[4]Mesa V.Strategies for Controlling the Work in Mathematics Textbooks for Introductory Calculus [J].Research in Collegiate Mathematics Education, 2010, (16): 235-265.

[5]Stevenson H W, Bartsch K.An Analysis of Japanese and American Textbooks in Mathematics [A].In: Leetsma R,Walberg H.Japanese Educational Productivity [C].Ann Arbor: Center for Japanese Studies, University of Michigan,1992.

[6]Son J.A Comparison of How Textbooks Teach Multiplication of Fractions and Division of Fractions in Korea and in the U.S.[A].In: Chick H L, Vincent J L.Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education [C].Melbourne: PME, 2005.

[7]Yeping Li.A Comparison of Problems That Follow Selected Content Presentations in American and Chinese Mathematics Textbooks [J].Journal for Research in Mathematics Education, 2000, 31(2): 234-241.

[8]Charalambos Y Charalambousa, Seán Delaney, Hui-Yu Hsu, et al.A Comparative Analysis of the Addition and Subtraction of Fractions in Textbooks from Three Countries [J].Mathematical Thinking and Learning, 2010, (12):117-151.

[9]日本文部科学省.高等学校学习指导要领（第四节数学）2009.http://www.mext.go.jp.

[10]刘绍学.普通高中课程标准实验教科书 数学1（必修）[M].北京：人民教育出版社，2008.