美国数学教师学科知识评价方法的述评

黄兴丰，马云鹏

（1.东北师范大学 教育科学学院，吉林 长春 130024；2.常熟理工学院 数学与统计学院，江苏 常熟 215500）

1986年，美国著名学者舒尔曼（Shulman）把学科知识（subject matter knowledge）定义为：“学科知识是指在特殊学科中的概念、原则与技能以及这些知识在教师头脑中的结构和数量.”[1]与此同时，美国开始出现研究，关注数学教师的学科知识对学生数学成绩的影响.这种趋势完全和逐渐兴起的一种观点相一致，即教师对学生学习的影响主要取决于学科知识，而不是一般知识或教学法知识[2～3].于是，有些研究者不再像原来一样使用教师的学历或选修的课程代表他们的学科知识水平[4]，而是直接采用数学考试来评价数学教师的学科知识.比如，马伦斯（Mullens）等曾做过一项研究，一共有72名小学教师和1 034名三年级学生参与其中.他们用这些教师当年毕业考试的数学成绩作为他们学科知识水平的依据.研究发现数学教师的学科知识对学生学习高级数学概念（除法与文字题、长度与体积、分数加法等）十分重要.马伦斯等解释说这种关系看起来应该是合乎逻辑的，因为只有当教师深刻理解之后，他们才有可能深入浅出地讲解[5].今天看来，这种评价的局限也是十分显然的.因为利用考试成绩，只能反映教师的计算能力和解决问题的能力.数学教师的学科知识是否仅仅局限于此？数学教师的学科知识究竟应当包括哪些关键性的要素？这些直至今日都尚未得到统一的认识.不过有一点是毋庸置疑的，教师至少应该掌握他们所教课程中的数学知识.

值得庆幸的是，近二十多年的研究已经得到一个共识，即教师拥有的学科知识，应当有别于学生或非教师职业人士的知识.自1986年舒尔曼（Shulman）提出并强调了学科知识在教学中的核心地位之后，他的观点引起了美国数学教育研究者的极大关注，同时也推进了美国数学教师学科知识评价方法的多元发展.

1 数学课堂观察

尽管，从表面上看来，课堂或教学录像的观察研究的是教师的课堂教学行为，而不是评价教师的知识.但是，通过对数学课堂或者录像的细致观察和深入分析，研究者可以洞察教师对学科知识的理解和认识，可以了解课堂教学实践与教师学科知识之间的重要关联.因此，课堂观察可以被认为是评价教师学科知识的方法之一.

一个经典的案例是雷哈特（Leinhardt）和史密斯（Smith）对专家教师课堂教学的研究[6].具体研究的对象包括4名专家教师和4名实习教师.在经历了3年时间的课堂观察之后，研究者确定了8名教师的学科知识水平：4名专家教师中的两个被评定为高水平，其余两个分别是中等水平和低水平，4名实习教师都处于中等以下的水平.为了进一步探索课堂教学行为和学科知识之间的相互关系，他们又从以下途径收集数据：（1）对8名教师进行了3个月的课堂观察，记录了大量的田野笔记，拍摄了10个小时的课堂录像；（2）要求教师对40个与分数有关的数学问题进行分类；（3）对教师进行访谈，访谈内容涉及分数的概念、分数的表征以及分数的恒等变化；（4）对3名专家教师（两个高水平，一个中等水平）关于分数化简的一节课进行了细致的分析.研究发现：专家教师比实习教师具备结构更精致的学科知识，而且随着教师对数学内容的深入理解，他们越来越能够连贯地把知识和课堂教学联系起来，更有利于促进学生的发展.这样的研究在之前的文献中是鲜见的.

博尔科（Borko）等也提供了一个评价数学教师学科知识的范例[7]，即从个人知识和信念，以及大学学习经历两个角度分析一名数学实习教师教学失败的原因.他们首先通过一周的课堂观察和访谈了解实习教师在课堂教学中的思考和行为.为了进一步掌握实习教师在大学的学习经历，他们特地去观察了数学教学法课堂，并采访了教学法教师以及教师培训项目的负责人.博尔科等还采用开放式的访谈，深入了解实习教师关于数学、教学、数学教学、数学学习等诸多方面的知识和信念，访谈中的所有问题都带有课堂教学情境的色彩，这样更有利于展现受访者的知识和信念.比如，当学生在计算分数除法遇到困难时——“我知道两个分数相除，应该把其中的一个分数颠倒，然后相乘.不过我不知道为什么除法一下子会变成了乘法，我也忘记了到底应该颠倒哪个分数”，教师应该如何帮助他们.研究发现，尽管实习教师对数学教学持有良好的信念，但是由于缺乏数学学科知识的深刻理解，因此难以实现教学目的.

最近，斯皮尔（Speer）和瓦格纳（Wagner）对大学微分方程的课堂进行了研究，试图探究教师的学科知识与学科教学知识（pedagogical content knowledge）对引导学生课堂讨论（小组或班级）的影响.他们认为，为了达到预定的教学目标，教师在引导学生展开讨论的过程中，必然会涉及如下的认知活动：第一，认识和理解学生正确或者错误的数学推理；第二，认识和理解学生的观点是否有利于推动课堂教学目标的完成；第三，认识和理解如何在学生已有观念的基础上发展他们对数学的理解.为了完成上述认知活动，教师必须依赖于他们自身的学科知识和学科教学知识.斯皮尔和瓦格纳对某数学家进行了个案研究，共收集了30个小时的课堂录像和18个小时的课后访谈.研究者最后根据录像和访谈确定教师未能成功引导学生开展讨论的4课录像，并对此进行5个步骤的精细分析.研究发现，即使拥有丰富教学经验和数学知识的教师，由于缺乏数学教学专门的学科知识（specialized content knowledge）与教学知识，在引导学生开展数学讨论的时候，还是会面临严峻的挑战[8].

从上面的研究范例可知，这些以个案为载体的课堂观察，确实揭示了数学教师学科知识对教学实践的重要意义.

21世纪初以来，美国许多教育研究机构开始着力于标准化课堂观察的研究，与前面课堂观察相比，其主要目的是试图全面掌握教师个体的教学状况.RTOP[9]（Reformed Teaching Observation Protocol）、ITC-COP[10]（Inside the Classroom Observation and Analytic Protocol）、QMI/MKT[11]（Quality of Mathematics in Instruction/ Mathematics Knowledge for Teaching）是美国当前具有代表性的3个课堂观察评价方案，从多个角度关注课堂教学的特点，不仅关注了课堂的教学特征，同时也强调了教学中学科知识的重要价值.比如，教师数学内容的讲解是否准确，教师传授的知识是否具有数学价值，教师是否突出了课堂的数学特征（数学表征、数学解释、数学抽象等），教师是否强调了数学知识和现实世界或者其它学科的联系（见表1）.

表1 标准化课堂评价方案对数学教师学科知识的观察点

尽管正如前面提到的那样，有学者质疑这些评价方案评定的不是教师学科知识本身，而是由学科知识形成的结果.但是，如果不否认教师的学科知识是课堂教学的基本要素之一，那么通过在课堂上观察教师如何使用学科知识，间接地评价他们的学科知识也是可行的.

事实上，课堂是教师展现学科知识的主要场所.因此，对于教师学科知识的评价而言，课堂观察无疑具有很高的效度.但是，无法避免的是观察者对学科知识的理解也会影响他们对教师评价的客观性.比如，教师课堂讲授的知识是否具有重要的数学价值？对于这个问题的理解，往往是因人而异的，依赖于观察者对数学的认识.再如，判断教师的数学解释是否合理准确，也依赖于观察者的数学知识，以及对评价方案的理解.也正是考虑到了这一点，ITC-COP项目组在观察者进入课堂之前，通常会花两天的时间进行培训.QMI/MKT研究小组则是花了将近两年的时间来讨论评价方案的适用性.RTOP课题组还提供了网上在线培训.值得提醒的是，为了评价教师的学科知识水平，往往需要评价者进行多次的课堂观察，否则很可能得到片面的结论.然而，实施大样本的课堂观察研究，需要大量的人力和物力，对任何研究者来说都是一个沉重的负担.

2 数学任务的访谈（以除法为例）

数学任务的访谈，也是评价教师知识常见的方法之一.用于评价教师学科知识的数学任务可以是书面的问题，也可以是口头访谈的一部分.下面，以除法为例，来说明这种研究方法的进展.

美国早期研究者采用的数学任务和用于考查学生的数学问题并无差别.比如，格雷伯（Graeber）、费希拜因（Fischbein）等设计的数学任务，乘法问题有12个，如：高速公路，汽车行驶的速度是2公里/分钟，假设车速不变，该车15分钟行驶多少路程？1公斤的洗涤剂可以生产15公斤的肥皂，0.75公斤的洗涤剂可以生产多少肥皂？除法问题有14个，如：5个朋友一共买了0.75千克的巧克力，平均每人多少？5个瓶子一共装了1.25升的啤酒，平均每瓶装多少[12]？格雷伯等一共对129名职前教师做了书面测试，接着访谈了其中的33人.在访谈中，首先研究者要求受访者回答类似于他们在书面测试中出错的问题.如果他们的回答还是错的，那么要求做出解释.一直到他们能够正确认识（或被告知）回答错误为止.然后，再要求受访者解释错误的原因[13].这种书面测试和临床访谈相结合的方法，可以帮助研究者深入了解教师理解数学知识的程度.但是，众所周知，“要给学生一杯水，教师得有一桶水”，教师从事数学教学所需要的学科知识的知识，远远不止学生掌握的数学知识.

迪罗西（Tirosh）等[14]在此基础上，对数学任务做了补充.在研究中，他们采用了两种不同的数学任务：第一，可用于考查学生的问题.除了前面提到的乘除法文字问题之外，他们还增加了两道计算题：0.38×5.15，3.75÷0.75；第二，6个命题的判断、解释或举出反例.这6个命题是：（1）在乘法中，积总是大于乘数；（2）0.45×90的积大于90；（3）在除法中，商一定小于被除数；（4）在除法中，除数一定是整数；（5）60÷0.65的商一定大于60；（6）70÷的商一定小于70.显然，第二种数学任务涉及数学证明和推理，需要教师深刻理解乘除法的意义.尽管教师通常不要求学生掌握这种知识，但是对于教师而言，这又是十分必需和特殊的数学知识.

鲍尔（Ball）继续深入探讨这种特殊的数学知识.她设计了如下的情境问题：（1）你能用哪些不同的方法计算1÷？（2）你能为1÷编写一个具有现实情境的问题吗？（3）假设学生问7除以0的商是多少，你该如何回答？（4）假设学生请你帮他解方程=5，如何教他[15]？诸如此类的问题，是教师在教学中经常会遇到的，为了帮助学生理解数学概念算法，纠正错误，教师需要这些不同于学生、数学家、以及其它行业人员的数学知识.

然而，数学任务的访谈，如同课堂观察一样，评价的过程同样依赖研究者的个人经历和知识，所谓“仁者见仁，智者见智”，很难形成统一的判断标准.其次，由于受到开放式访谈，以及数学任务数量的限制，很难控制研究的信度和效度，获得的结论难以推广.再者，尽管现在使用的数学任务都具有教学情境的特征，但是这毕竟不是真实的课堂，教师在任务上的表现是否和课堂教学的表现相一致，还值得进一步探讨.

即便这样，从发展的角度来看，这种研究方法已经揭示了数学教学究竟需要什么样的学科知识？数学教师，不仅应当掌握学生应该掌握的数学知识，而且还要深刻理解数学知识背后的原理，掌握解决问题的思想和方法，并能在不同的情境中灵活应用.

3 标准化的测量

近来，美国的研究者一致认为数学教学需要一种特殊而复杂的知识，他们把它概括为数学教学知识（mathematics knowledge for teaching，简称MKT），并各自发展了不同的概念框架.与此同时，美国的研究者又产生了一个新的研究渴望，试图发展有效的测量工具来评价数学教师的MKT水平.于是，标准化的测量问卷立刻受到了众多研究机构的青睐.

如今，在美国具有较大影响力的评价工具有SII/LMT[16]（Study of Instructional Improvement/Learning Mathematics for Teaching）、DTAMS[17]（Diagnostic Teacher Assessments in Mathematics and Science）、KAT[18]（Knowing for Algebra Teaching）与Scaling Up SimCalc[19].在这4种评价工具中，除了DTAMS和KAT中含有部分简短的问答题之外，其余测试题都是标准化的选择题，并且每个问题的答案只作正确和错误之分，因此使用起来十分方便，很容易获得大样本的数据，计算评价工具的信度和效度.

值得提醒的是，在上述4种评价工具中，有一点是一致的，即学科知识始终是数学教学知识不可或缺的重要部分.不过，他们对学科知识的认识还是不尽相同的.

3.1 SII/LMT中的学科知识

SII/LMT把MKT分成学科知识和学科教学知识两大部分（如图1）.其中学科知识又包含3类：一般的学科知识（common content knowledge）、专门的学科知识（specialized content knowledge）和横向的数学知识（knowledge at the mathematical horizon）[20].

首先，一般的学科知识是指数学教师和学生同样具有的数学知识.例如，李老师发现新的数学教科书比原来的教科书更加强调“0”这个数.于是他设计了一些和“0”有关的命题，打算让学生判断正误.你认为下列哪些命题是正确的？（请选择“正确”、“错误”或者“我不确定”作为你的判断）（1）0是一个偶数；（2）0不是一个数，但是可以作为数字的占位符；（3）8可以写成008.

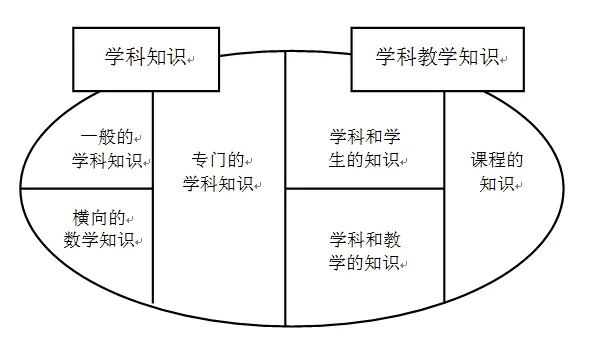
图1 SII/LMT的概念框架

第二，专门的学科知识是指教师教学所需要的数学知识，应当区别于其它职业人士（比如会计、工程师）的数学知识.比如，学生在做两位数乘法的时候，一共出现了如下3种方法（如图2）.请问其中哪些方法可以用来计算任何两位数的乘法？

图2 计算两位数的乘法

从上面所举例子中可以看到，教师在分析学生的错误，或在判断非标准的算法是否可以推广的时候，需要一种特殊的数学知识.这样的知识在许多教学情境中，都是不可或缺的.譬如：（1）讲解数学概念；（2）回答学生提出的“为什么”；（3）运用例子，使得数学知识具体化；（4）识别具体表征中的要素；（5）把表征和潜在的概念相联系，而且在不同表征之间建立关系；（6）把所教的知识与前后的知识相联系；（7）向家长解释数学教学的目的和意义；（8）评价和改编教科书中的数学内容；（9）简化和加深数学任务的难度；（10）评价学生论断的合理性；（11）提供数学解释；（12）选择便于使用的数学定义；（13）反思数学符号语言使用的合理性；（14）提出有意义的数学问题；（15）按照具体的目标选择表征；（16）检验数学的等价性.上述任何一项任务都是教师常规性工作的组成部分，这些工作需要特殊的数学理解和推理[21].

第三，横向的数学知识，类似于克莱因（Klein）所说的“高观点下的初等数学”知识.比如，冉司克斯（Zazkis）曾经举过一个例子：老师请三年级的学生数如图3中有多少个三角形，有一组学生数到32个，还有一组却数到27个.尽管老师事先没有数过，但是她却可以根据旋转对称的知识，判断这些回答都是错误的，因为三角形的个数一定是5的倍数[22].

比如，9年级的学生问：“为什么随着|x|的增大，抛物线y=x2和y=x2+1看起来是无限靠拢的？”这就需要教师具备极限、导数等高等数学知识，否则很难做出合理的解释.不妨在坐标轴的右侧作直线x=x0，交两抛物线于A、B两点.并过A、B作抛物线的切线，同时过B点作抛物线y=x2+1的法线，与抛物线y=x2在A点的切线相交于点C（如图4）.显然，无论x0如何变化，|AB|=1.事实上，图像的靠拢实际上是由抛物线法线方向的距离引起的.如在B点可以用|BC|来近似表示.此时，两条切线的斜率为k=2x0，tan∠ABC=k=2x0，于是有：

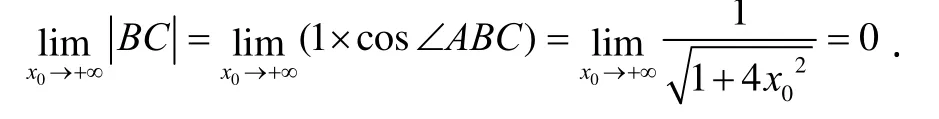
图3 正五边形中三角形个数

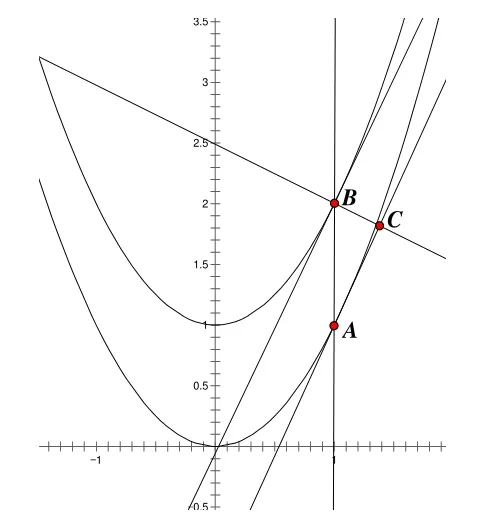
图4 平移的抛物线

正如鲍尔等指出的那样，横向的数学知识实质上就是数学教师对高等数学知识的初步理解和认识，它有利于教师从更广阔、更特殊的视角理解数学教学.具体而言，这种知识有利于教师：（1）判断数学知识的重要意义；（2）倾听学生回答的数学价值；（3）突出数学知识的重点；（4）在不同的数学知识之间形成联系；（5）评价数学知识的地位；（6）抓住数学错误的本质.尽管横向的数学知识在概念上有所论述，但是SII/LMT如今还尚未形成一套比较成熟的测试题.最后值得指出的是，鲍尔等人关于MKT的研究也已经引起了其它国家研究者的高度重视[23].

3.2 DTAMS中的学科知识

DTAMS也把MKT分成两部分，即学科知识和教学教学知识.其中有四分之三的测试题评价的是教师的学科知识，而且DTAMS中所界定的学科知识就是教师所教的数学知识，也就是前面SII/LMT中一般的学科知识.这些数学知识在DTAMS的测试题中被分成了3类：

第二，概念性的理解.例如，哪两个数在1.35和1.36之间？（A 1.3和1.；B 0.351和0.352；C 1.345和1.354；D 这两个数之间没有其它数）

第三，高水平的思维.例如，矮先生身长3枚回形针，高先生身高5颗纽扣.如果2颗纽扣和3枚回形针一样长，请问高先生身高多少枚回形针？请写出解答过程.

3.3 KAT中的学科知识

在KAT的概念框架中一共有3个维度（如图5），分别是：代数内容（algebra content）、数学知识域（domain of mathematical knowledge）和代数教学知识（algebra knowledge for teaching）.其中学科知识可以分成两类：

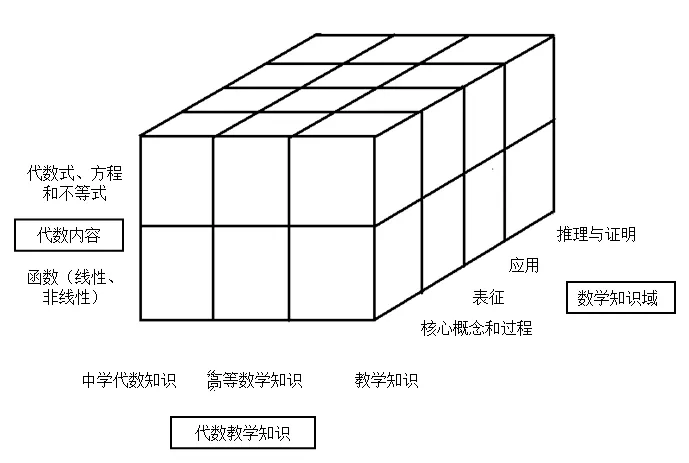
图5 KAT的框架

第一，中学代数知识，即教师所教的数学知识，也就是一般的学科知识.例如，下面哪个情境可以用指数型函数来表示？（A小球自由下落t秒后的高度h；B假设某社区平均每年增长人数n，t年后社区的人口数p；C某种品牌轿车，平均每年降价d%，t年后轿车价格V）

第二，高于中学数学课程的高等数学知识（advanced knowledge），类似于前面所说的横向的数学知识.例如，在下列哪个集合中，命题“若ab=0，则a=0或b=0”总成立？（A 实数集；B 复数集；C [6]；D [5]；E 2×2实矩阵）

3.4 Scaling Up SimCalc中的学科知识

Scaling Up SimCalc把MKT分成6类，包括：（1）解释非常规的数学表征；（2）选择能反映课程核心观念的问题和例子；（3）区分日常语言和数学语言的使用；（4）在不同的表征之间形成联系；（5）理解模型和表征的意义；（6）评价数学命题的合理性.尽管Scaling Up SimCalc没有对数学教师的学科知识进行明确的划分，但是测试题还是可以分成以下3类：

第一，要求教师分析学生的特殊解法，这相当于SII/LMT中专门的学科知识.例如，张老师要求学生根据表格中的x和y的比列关系（如图6所示），在空格中填上相应的数据.有一个学生是这样计算的：x=6，y==24.请问这个方法在什么条件下总是可行的？（A 只有当x和y都是整数时；B 只有当表中最后两行的数据都是偶数时；C 只有当表中最后一行的数据是它前一行数据的两倍时；D 只要x和y满足比列关系；E 只要y是x的一次函数）

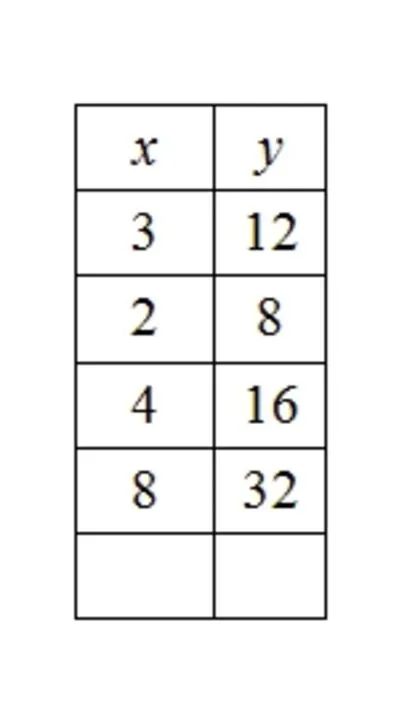
图6 分析学生特殊解法

第二，要求教师对数学关系或图像做出解释.这些问题评价的教师学科知识往往介于一般的学科知识和专门的学科知识之间，很难做出区分.比如，黄老师要求学生解释为什么图7中路程与时间的函数图像（横轴表示时间，纵轴表示路程）表示的不是比例关系.学生的下列解释哪些是正确的？（A 图像不可能是曲线；B 路程和时间之间的关系不可能总是不变的；C 图像画得不好；D 曲线上不同点处路程与时间的比值不同；E 曲线上路程与时间的比不总是一个常数）

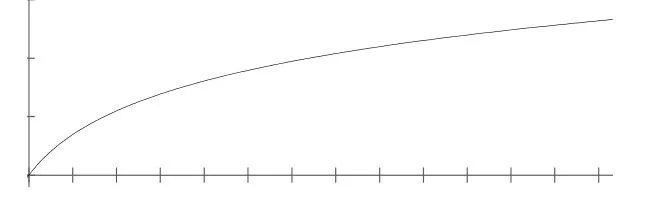
图7 解释函数图像

第三，要求教师解答和和学生一样的数学题，也就是一般的学科知识.在此不再赘述.

以上的分析表明，研究者对于数学教师学科知识的认识，尽管已经有了长足的发展，但尚未形成统一的认识，仍然缺乏明确的理论指导.因此，很难让人信服它们所评价的范畴就是数学教师学科知识的所有方面.而且，教育现象是复杂多变的，比如就判断学生的错误而言，学生在课堂上误解知识可能是由自身的学习经验，以及所学知识的复杂性引起的.因此，简单对错的判断很难如实反映教师的学科知识水平.评价工具中标准化的选择以及简短的反馈，在美国已经受到了不少教师的抵制.他们认为教师的知识既是內隐缄默，又是情境化、实践性的，许多重要的方面不是仅靠标准化的选择或简短的问答所能评价的.他们毫不留情地批评道：采用标准化的评价工具，事实上就是对教师知识的藐视和践踏.

4 结 语

美国关于数学教师学科知识的评价已经经历了比较长的历史发展，发展了多种评价的方法，对数学教师学科知识的认识也发生了深刻的变化.不过，各种方法的利弊也是显然的，尚缺乏强有力的理论指导，因此多种方法的综合使用可能是目前数学教师学科知识评价的最佳选择.

[1]Shulman L S.Those Who Understand: Knowledge Growth in Teaching [J].Educational Researcher, 1986, (15): 4–14.

[2]Greenwald R, Hedges L V, Laine R D.The Effect of School Resources on Student Achievement [J].Review of Educational Research, 1996, (6): 361–396.

[3]Hill H C, Sleep L, Lewis J M, et al.Assessing Teachers’ Mathematical Knowledge: What Knowledge Matters and What Evidence Counts? [A].In: Lester F K.Second Handbook of Research on Mathematics Teaching and Learning [C].Charlotte, NC: Information Age Publishing, 2007.

[4]Strauss R P, Sawyer E A.Some New Evidence on Teacher and Student Competencies [J].Economics of Education Review, 1986, (5): 41–48.

[5]Mullens J E, Murnane R J, Willett J B.The Contribution of Training and Subject Matter Knowledge to Teaching Effectiveness: a Multilevel Analysis of Longitudinal Evidence from Belize [J].Comparative Education Review, 1996,(40): 139–157.

[6]Leinhardt G, Smith D A.Expertise in Mathematics Instruction: Subject Matter Knowledge [J].Journal of Educational Psychology, 1985, (77): 247–271.

[7]Borko H, Eisenhart M, Brown C A, et al.Learning to Teach hard Mathematics: Do Novice Teachers and Their Instructors Give up Too Easily? [J].Journal for Research in Mathematics Education, 1992, (23): 194–222.

[8]Speer N F, Wagner J F.Knowledge Needed by a Teacher to Provide Analytic Scaffolding During Undergraduate Mathematics Classroom Discussions [J].Journal for Research in Mathematics Education, 2009, (40): 530–562.

[9]Sawada D, Pilburn M.Reformed Teaching Observation Protocol [Z].2000.

[10]Horizon Research.Inside the Classroom Observation and Analytic Protocol [Z].2000.

[11]Learning Mathematics for Teaching Project.A Coding Rubric for Measuring the Quality of Mathematics in Instruction[Z].2006.

[12]Fischbein E, Deri M, Nello M S, et al.The Role of Implicit Models in Solving Verbal Problems in Multiplication and Division [J].Journal for Research in Mathematics Education, 1985, 16(1): 3–17.

[13]Graeber A O, Tirosh D, Glover R.Preservice Teachers’ Misconceptions in Solving Verbal Problems in Multiplication andDivision [J].Journal for Research in Mathematics Education, 1989, 20(1): 95–102.

[14]Tirosh D, Graeber A O.Preservice Elementary Teachers’ Explicit Beliefs about Multiplication [J].Educational Studies in Mathematics, 1989, (20): 79–96.

[15]Ball D L.The Mathematical Understandings That Prospective Teachers Bring to Teacher Education [J].Elementary School Journal, 1990, (90): 449–466.

[16]Learning Mathematics for Teaching Project.Measures of Teachers’ Knowledge for Teaching Mathematics [EB/OL].http://www.sitemaker.umich.edu/lmt, 2011–02–15.

[17]Saderholm J, Ronau R, Brown E T, et al.Validation of the Diagnostic Teacher Assessment of Mathematics and Science(DTAMS) Instrument [J].School Science and Mathematics, 2010, 110, (4): 180–192.

[18]Knowing Mathematics for Teaching Algebra Project.Survey of Knowledge for Teaching Algebra [EB/OL].http://www.msu.edu/～kat, 2011–08–21.

[19]Shechtman N, Roschelle J, Knudsen J, et al.SRI Teaching Survey: Rate and Proportionality [EB/OL].http://ctl.sri.com/publications, 2011–06–21.

[20]Hill H C, Ball D L, Schilling S G.Unpacking Pedagogical Content Knowledge: Conceptualizing and Measuring Teachers’ Topic-specific Knowledge of Students [J].Journal for Research in Mathematics Education, 2008, (39):372–400.

[21]Ball D L, Thames M H, Phelps G.Content Knowledge for Teaching: What Makes It Special? [J].Journal of Teacher Education, 2008, (59): 389–407.

[22]Zazkis R, Mamolo A.Reconceptualizing Knowledge at the Mathematical Horizon [J].For the Learning of Mathematics,2011, (2): 8–13.

[23]Beswick K, Callingham R, Watson J.The Nature and Development of Middle school Mathematics Teachers’ Knowledge[J].Journal of Mathematics Teacher Education, 2012, (15): 131–157.