第一性原理计算水对缬氨酸电子结构的等效势

郑浩平，吴丽华，李 根

（同济大学 物理系，上海 200092）

蛋白质分子的电子结构对研究蛋白质分子性质及其生物活性有重要意义，但其计算量极其巨大.过去20多年里，计算凝聚态物理和量子化学领域中对一类所谓的O（N）（计算量正比于系统所含粒子数N）方法很有兴趣.团簇埋入自洽计算（selfconsistent cluster-embedding calculation，SCCE）［1-2］方法是其中一种，它基于密度泛函理论，属“第一性原理、全电子、从头计算”法.SCCE方法得到的单电子波函数是局域化的，也就是说，每个单电子波函数只局域于系统的某个部分.该方法有两个优点：①材料中的局域化价电子可很好地被SCCE计算得到的局域化波函数描述；②适用于任何复杂系统，可在不降低计算精度的条件下极大地减少计算量.这使得在现有超级计算机上计算蛋白质分子的电子结构成为可能.用SCCE方法已经算出了三个较小的蛋白质分子的电子结构［3-6］.

尽管SCCE方法极大地减小了计算量，但把大量水分子直接添加到蛋白质分子电子结构的计算中，其计算量仍十分巨大.另一方面，虽然已有一些课题组在考虑水溶液影响的基础上发展了若干水溶液的连续介质模型［7-8］，但它们主要用于计算蛋白质分子的折叠过程和空间结构.研究者所关心的是蛋白质分子在溶液环境下、已具有稳定空间结构时的电子结构.最后，考虑到蛋白质分子的活性部位及其局域分子轨道在空间尺度上与一个水分子相当，显然不能把水分子近似成一个导体样、可极化的连续介质，这里确实需要仔细考虑各个最近邻水分子的影响.因此需要一个新的、简单易用、几乎不增加计算量又能很好地模拟水溶液对蛋白质分子电子结构影响的等效势.

自然界中的蛋白质分子有几十万种，基本上由20种氨基酸组成.因此只需构造水溶液对20种氨基酸电子结构的等效势，就可应用于各种蛋白质分子电子结构的计算.已经有15种氨基酸得到了研究：半胱氨酸 （Cys），赖氨酸 （Lys＋），组氨酸（His），谷氨酸 （Glu-），丙氨酸（Ala），天冬氨酸 （Asp-），丝氨酸 （Ser），苏氨酸 （Thr），天冬酰胺 （Asn），甘氨酸（Gly），亮氨酸（Leu），精氨酸（Arg＋），脯氨酸（Pro），异亮氨酸（Ile）和酪氨酸（Tyr）［9-19］.本文将构造水溶液对另一个氨基酸——缬氨酸（Val）电子结构的等效势.缬氨酸是疏水性的、非极性氨基酸，有19个原子，其侧链是一个异丙基.缬氨酸在水溶液中不带电.

本文首先用“自由团簇计算法”计算缬氨酸和水分子系统总能量最低时的空间结构；其次，基于上一步的空间结构，用SCCE方法算得水分子外势下缬氨酸的电子结构；最后用偶极子代替水分子，调节偶极子的电荷值和位置，构建水溶液对缬氨酸电子结构的等效势.

1 理论模型

本文所用的自由团簇计算法和SCCE方法已在文献［1，19］中有详细叙述，这里仅作简单介绍.

根据密度泛函理论（DFT）［20-21］，一个含N 个电子和M 个固定原子核的系统总能量可写成（不含相对论效应，本文采用固体物理学中的原子单位制：e2＝2，ħ＝1，2me＝1；能量单位为 Rydberg常数：

式中：ρ是电子密度，r，r′是空间坐标，Rj和Zj分别是第j个原子核的空间坐标和电荷值，Tni［ρ］是无相互作用电子系统的动能，Exc［ρ］是交换-关联能.在推导式（1）时，Kohn等已假定存在一个“无相互作用电子系统”，其基态电子密度等于真实系统基态电子密度ρ［21］.现在，每一个无相互作用电子可用一个定态单电子波函数（r）描述，“无相互作用电子系统”的电子密度和动能可写成

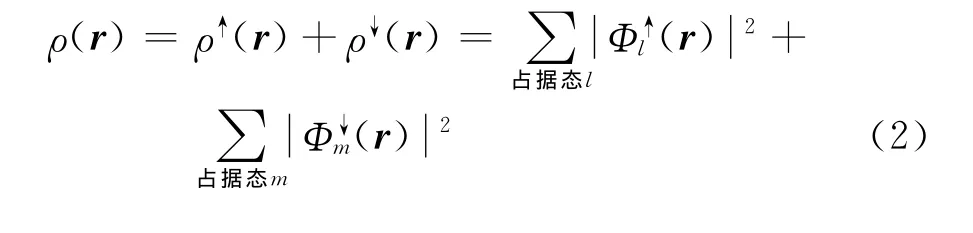
存在二种无相互作用电子：扩展的和局域化的，它们满足不同的边界条件，并对应不同的计算方法.

1.1 扩展的

限定每一个无相互作用单电子波函数Φσn（r）扩展于系统所占有的全部空间.在此模型下，对理想晶体，Φσn（r）满足周期性边界条件，则方程（4）中的单电子哈密顿具有ρ（r）的周期性，布洛赫定理成立，能带计算得以进行.对一个自由团簇，方程（4）在边界条件下求解，此时单电子哈密顿具有自由团簇的点对称性.

1.2 局域化的

现在考虑第i个被埋入团簇，其他（k-1）个被埋入团簇被看作固定的环境，其原子称为周围原子，每个周围原子有个芯区.第i个被埋入团簇的电子密度用ρ1（r）表示，其他（k-1）个被埋入团簇的电子密度用ρ2（r）表示（分布区域与ρ1（r）有小的交叠）.由于所有N 个（r）都是局域化的，有（N＝N1＋N2）

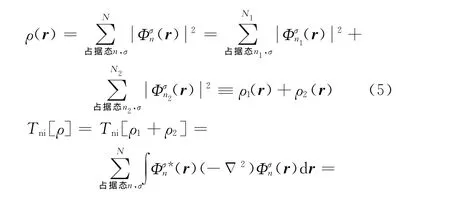
在式（1）右边加上一个等于零的积分∫ρ1（r）Vor（r）dr，结合式（5）和（6），假定ρ2（r）固定，现在对式（1）的变分就得到SCCE方法的基本方程［1］

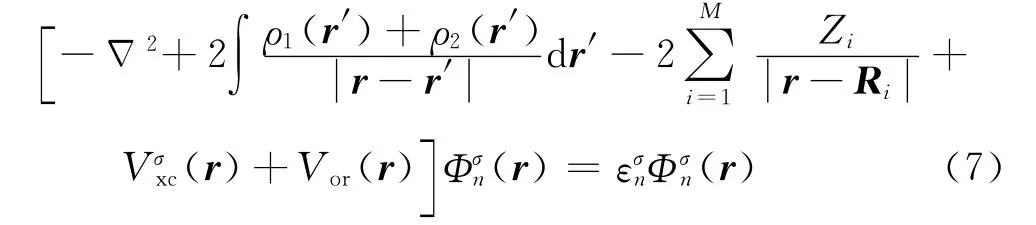
可以证明：方程（7）就是带有特殊边界条件（9）和（10）的Kohn-Sham方程（4）.对一个真实有限系统，二个边界条件对不同的被埋入团簇是不一样的.依次解出所有k个被埋入团簇，方程（7）给出整个系统的一组完整的单电子波函数，它使式（1）的总能量最小.可看文献［19］以更详细地了解密度泛函理论、自由团簇计算法和SCCE方法.

2 计算过程和结果

2.1 确定Val＋7H2O系统的空间位形

本文用Val＋7H2O系统来模拟水溶液中的缬氨酸系统.当然，就水溶液中缬氨酸几何结构的自由度来说，7个水分子是不够的.但这里不是要模拟室温下水溶液中缬氨酸的结构变化，而是要构建水溶液对缬氨酸电子结构的等效势.从电子结构角度来说，只需考虑如下7个水分子：它们都处于Val的最近邻位置，与Val形成氢键，并使Val＋7H2O系统总能量最小.理由如下：①在计算中，Val已具有其水溶液中的空间结构且保持不变.②由于Val周围最近邻空间的有限性和氢键的饱和性，只有有限个水分子能跟Val形成氢键.事实上，用了7个水分子后，Val中的H和O原子已经全部和水分子形成氢键.③虽然室温下水分子在不断振动、运动，但根据统计力学，它们有最大概率处在使系统能量最低的位置.④距离较远的极性水分子的偶极子势以1／r2的速度衰减.所以不管位于远处的其余水分子如何分布，至少作为一级近似，这7个水分子已经给出了水溶液对Val电子结构的主要影响.所以，7个水分子处在上述位置时的Val的电子结构可近似看作是水溶液中Val的电子结构.

水溶液中缬氨酸的19个原子空间坐标在表1中给出.它取自洛克菲勒大学质谱技术及气相离子化学实验室提供的PDB格式文件（http：／／prowl.rockefeller.edu／aainfo／struct.htm）.

表1 缬氨酸各原子坐标Tab.1 Atomic coordinates of valine

在中性溶液（pH＝7）中，氨基得到一个质子变为H3N＋，羧基失去一个质子变为COO-.水分子是极性的，主要影响缬氨酸的氨基、羧基及侧链.开始时，7个水分子是半随机分布的：H3N＋附近3个，COO-附近1个，侧链附近3个.每个水分子都和缬氨酸形成氢键，使Val＋7H2O系统有较低能量.

所有计算采用von Barth 等［22］提出的、由Rajagopal及其合作者［23］进行了再参数化的交换-关联势.计算所用的C，N，O，H四类原子的优化高斯基函数与计算蛋白质分子电子结构时所用的相同［3-6］：碳原子为8s6p，26个高斯基函数；氮原子为8s7p，29个高斯基函数；氧原子为8s7p，29个高斯基函数；氢原子为8s1p，11个高斯基函数.整个Val＋7H2O系统共取695个高斯基函数.为了对交换-关联势Vxc进行数值计算，系统所在空间被分割成440002个格点.

计算所用的自由团簇计算程序由美国路易斯安纳州立大学物理系的卡拉威教授研究组开发［24］.对Val＋7H2O系统自洽求解后得到系统的电子结构、总能量及每个原子受力情况.

在对Val＋7H2O系统空间位形优化的过程中有三个限制：①Val的几何结构固定不变；②水分子的几何结构固定不变；③调节Val和水分子的相对位置时，水分子只能处在Val的最近邻位置附近.7个水分子根据受力逐个调节.每个水分子在调节过程中，沿受力方向一次性取12个由近到远的位置，以避免水分子落入某个局部极小区域.调完7个水分子算一轮.经过近百轮的调节，Val＋7H2O系统能量达到最低，Val＋7H2O系统的空间位形也就确定了.

计算结果得Val＋7H2O系统最终位形的能量是-1865.9726 Ry.图1为最终空间位形（Val原子标号根据表1标出）.

图1 Val＋7H2O系统的最终空间位形图Fig.1 Final configuration of Val＋7H2O system

当然，即使再做上百轮计算，也不能绝对地说已得到能量最低的空间位形.但可以确信上述空间位形的系统总能量已经非常接近最低能量了.因此，在上述7个水分子势下Val的电子结构可以近似看作水溶液中Val的电子结构.理由如下：第一，本文不研究Val和水分子的相对位置.第二，室温下，不存在蛋白质分子和水分子之间固定的氢键，所以蛋白质分子和水分子之间也没固定相对位置.水分子只以最大概率处在使系统能量最低的位置.第三，为了减小计算量，在基于密度泛函理论的自由团簇计算和能带计算中都采用了电子密度拟合技术：用一个赝电子密度来求解系统的电子结构.该赝电子密度不同于真实电子密度，但用它求出的系统总能量与用真实电子密度算出的系统总能量非常接近.人们认为由这样的赝电子密度求出的电子结构是系统真实电子结构的很好近似.

2.2 水分子势下Val的电子结构

基于上一节所确定的Val＋7H2O系统的空间位形，将整个系统分为八个团簇，Val为第一个团簇，每个水分子各作为一个团簇，进行SCCE计算.和自由团簇计算相比，SCCE计算使用相同的势，只是单电子波函数变成局域的，这样就从Val＋7H2O系统中分离出Val的电子结构.计算所用的SCCE计算程序为本课题组自主开发［25］.

计算采用分块-合拢技术，含两种形式的自洽循环：团簇内循环和团簇间循环.共进行了十轮团簇间循环，计算收敛，得到水分子势下Val费米面附近10个单电子态的能级和Mulliken分析值（布居数）.

2.3 用偶极子构建等效势

由于偶极子可以方便地加到SCCE计算中，并且几乎不增加计算量.另一方面，极性水分子的势可以合理地用偶极子势模拟.因此选择偶极子来构建等效势.

把第2.2节中七个团簇中的水分子用偶极子代替：水分子中氧原子的位置放一个负电荷，两个氢原子连线中点放一个正电荷.七个偶极子的初始电荷值都设定为0.5 e，正负电荷间距离为L＝0.05858 nm，并且固定不变.调整偶极子的电荷值及其空间位置，重新计算缬氨酸的电子结构.计算仍用SCCE计算程序，但因偶极子没有电子，不需进行团簇间循环，只需对含缬氨酸的第一个团簇进行团簇内循环计算.

需要注意的是第2.1节的结果不能作为本节调节偶极子的标准，因为这两个系统包含的电子数目不同，每个电子的分布区域也不一样.第2.2节用SCCE方法得到的结果才是标准.为了判定现在算出的Val电子结构和第2.2节中算出的Val电子结构的差别，设定以下两个判据：

（1）能量本征值的均方差

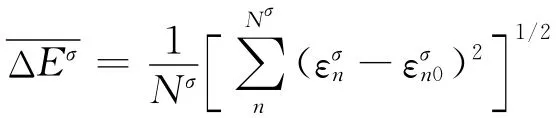
（2）电荷密度的等效均方差

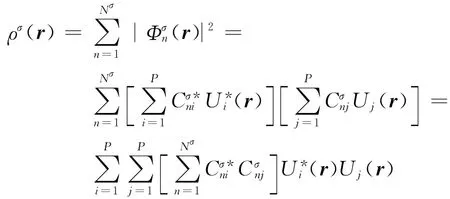
二次计算所用的展开基函数Ui（r）相同.由于计算中采用的“电荷拟合技术”［24，26］降低了判据（2）的可靠性，所以主要采用判据（1）.

用SCCE方法进行Val团簇内循环计算，就可得到Val在七个偶极子势下的电子结构，然后求出上述两个判据的值.逐次调节七个偶极子的电荷及空间位置，使上述两个判据减小.经过反复许多轮调节后，能量本征值均方差由最初的2.4823×10-3下降到了1.6082×10-3.这样便用偶极子势构造了水溶液对缬氨酸电子结构的等效势.表2给出了七个偶极子的最终电荷值和坐标值.同时也得到了偶极子势下缬氨酸费米面附近10个能级的本征值及Mulliken分析值.

几十年来，已有许多文献讨论了如何用点电荷水分子模型模拟水溶液的问题.Guillot在他的综述文章中列出了多达46种不同的点电荷水分子模型［27］，这实际上间接表明了点电荷水分子模型在定量描述真实水溶液性质方面的不成功.在之前构造等效势的研究中［11，13，15］，除了偶极子，研究者还尝试使用了两种较流行的3点电荷水分子模型（TIP4P-FQ［28］与SPC［29-30］）.但计算显示：更为复杂的3点电荷水分子模型未能给出比偶极子更好的结果，此问题将另文讨论.

3 讨论

为了讨论水溶液对缬氨酸电子结构的影响，研究者用自由团簇计算法计算了一个无外势的、孤立缬氨酸的电子结构，系统总能量为-800.5700 Ry.同时也得到了其费米面附近十个本征态的能量和Mulliken分析值.

表3给出了缬氨酸在三种条件下（偶极子势、水分子势和无外势）费米面附近第25到34能级的能量本征值，最后一行是费密面上的能隙：Eg＝E33-E32.图2是偶极子势、水分子势和无外势条件下缬氨酸电子能级的比较示意图.

缬氨酸的性质主要由费米面附近的电子态所决定.Mulliken分析值表明在偶极子势和水分子势下，Val费米面以下各分子轨道的成分非常相似：第32，31两个态主要被羧基的氧2p电子占据；第30态是个杂化态，主要被羧基的氧2p电子和Cα的2p电子占据；第29，28两态主要被侧链的碳2p电子占据；第27态主要被侧链的碳2p电子、氢1s电子和Cα的2p和1s电子占据；第26态是杂化态，主要被羧基的碳2p电子、氧2p电子及4号碳原子的2p电子、17号氢原子的1s电子占据；第25态主要被3，4号碳原子的2p电子及16，19号氢原子的1s电子占据.但是对于孤立的缬氨酸，三个分子轨道有所不同：第29态主要被羧基的氧2p和碳2p电子占据；第27态是个杂化态，主要被2，3，4号碳原子的2p电子及18号氢原子的1s电子占据；第25态也是个杂化态，主要被羧基的氧和碳2p电子、4号碳原子的2p电子及17号氢原子的1s电子占据.

图2 缬氨酸在不同外势下能量本征值比较Fig.2 Comparison of eigenvalues of valine in different potentials

比较表3的第二列和第三列，以及图2a，b，可以看出水溶液并没有改变各电子态的相对位置.水溶液的主要影响是将缬氨酸费米面以下八个能态平均提升了约0.0570 Ry，将能级扩大了约30.37%.

比较表3的第三列和第四列，以及图2b，c，可以看出以偶极子势为外势时，费米面下各能级本征值与以水分子势为外势的各能级本征值很接近，只有第29态的能级升高了约0.0118 Ry.此外，用偶极子势算得的能隙比用水分子势算得的能隙扩大了约19.73%.由于未占据态对电子密度无贡献，因此可以认为偶极子势较好地模拟了水分子势对缬氨酸电子结构的影响.

4 结论

用第一性原理、全电子、从头计算方法计算了水溶液对缬氨酸电子结构的等效势.主要涉及三个步骤：第一，用自由团簇计算方法得到能量最低时水分子与缬氨酸的相对空间位形；第二，在此空间位形的基础上，用SCCE计算缬氨酸在水分子势下的电子结构；第三，用偶极子代替水分子，并进行调节，使缬氨酸在偶极子势下的电子结构尽量接近水分子势下的电子结构.

比较水分子势、偶极子势、无外势三种情况下缬氨酸的电子结构，水溶液对缬氨酸电子结构的影响如下：使费米面下八个能级平均提升约0.0570 Ry（0.7755eV），使能隙扩大30.37%.由于水分子势下和偶极子势下的费米面以下能态结构很相似，所以偶极子势可以较好地模拟水分子势.因此，基于第一性原理、全电子、从头计算方法，构造了一个简单易用、几乎不增加计算量、可模拟水溶液对缬氨酸电子结构影响的偶极子势.

水溶液对20个氨基酸电子结构的等效势很快将被全部构造完毕.它们可被直接运用于溶液中蛋白质分子的电子结构计算，是基于分子中“局域化电子”的存在.大量事实表明，分子有许多性质是与局域化电子相联系的.这类性质有明显的“加和性”和“恒定性”：分子整体的性质相当精确地等于局部性质之和，而这种局部性质与某种局部结构单元有相当固定的联系，即不论该局部结构单元出现在什么分子中，它对分子这种性质的贡献几乎是不变的.例如，所有饱和烃中C—H和C—C键的键能几乎都是一样的，分子的总键能几乎严格等于各键键能之和.另外，蛋白质分子的活性部位的存在也表明在这些部位有局域化价电子.蛋白质基本上含20种氨基酸：每个氨基酸有一个N端、一个C端和一个侧链；氨基酸脱水（变成氨基酸残基）缩合构成多肽链，每条多肽链有一个N端、一个C端和许多侧链；一个蛋白质分子由一条或多条多肽链组成.对处于蛋白质分子内部的N端、C端和侧链，因屏蔽作用，不用考虑水溶液的影响.而对处于蛋白质分子表面的N端、C端和侧链（活性部位都在这些位置），可合理地认为其局部结构及其局域化价电子态与相应的孤立氨基酸几乎相同.因此，可把对单个氨基酸构造的水溶液等效势应用于已组合成蛋白质分子的且处于蛋白质分子表面的氨基酸残基的N端、C端和侧链.

［1］Zheng H.One-electron approach and the theory of the selfconsistent cluster-embedding calculation method［J］.Physics Letters A，1997，226：223.

［2］Zheng H.Self-consistent cluster-embedding calculation method and the calculated electronic structure of NiO ［J］.Physical Review B，1993，48（20）：14868.

［3］Zheng H.Electronic structure of trypsin inhibitor from squash seeds in aqueous solution［J］.Physical Review E，2000，62（4）：5500.

［4］郑浩平.蛋白质分子电子结构的第一性原理从头计算 ［J］.物理学进展，2000，20：291.ZHENG Haoping.Ab initio calculation of the electronic structure of protein［J］.Progress of Physics，2000，20：291.

［5］Zheng H.Ab initio calculation of the electronic structures and biological functions of protein molecules［J］.Modern Physics Letters B，2002，16（30）：1151.

［6］Zheng H.Electronic structures of Ascaris trypsin inhibitor in solution［J］.Physical Review E，2003，68（5）：051908.

［7］Eckert F，Klamt A.Fast solvent screening via quantum chemistry：COSMO-RS approach ［J］.AIChE Journal，2002，48（2）：369.

［8］Foresman J B，Keith T A，Wiberg K B.Solvent effects.5.influence of cavity shape，truncation of electrostatics，and electron correlation on ab initio reaction field calculations［J］.The Journal of Physical Chemistry，1996，100（40）：16098.

［9］Wang X，Zheng H，Li C.The equivalent potential of water molecules for electronic structure of cysteine ［J］.The European Physical Journal B，2006，52（2）：255.

［10］Li C，Zheng H，Wang X.The equivalent potential of water molecules for electronic structure of lysine ［J］.Science in China G，2007，50（1）：15.

［11］Li C，Zheng H，Wang X.The equivalent potential of water molecules for the electronic structure of histidine［J］.Journal of Physics：Condensed Matter，2007，19（11）：116102.

［12］Zhang T，Zheng H，Yan S.Equivalent potential of water molecules for electronic structure of glutamic acid［J］.Journal of Computational Chemistry，2007，28（11）：1848.

［13］闫述，郑浩平，张甜.水溶液势对丙氨酸电子结构影响的模拟［J］.科学通报，2008，53（7）：758.YAN Shu，ZHENG Haoping，ZHANG Tian.Simulation of the effect of water on the electronic structure of alanine ［J］.Chinese Science Bulletin，2008，53（7）：758.

［14］Zhang T，Zheng H，Yan S.Equivalent potential of watermolecules for electronic structure of aspartic acid［J］.Journal of Computational Chemistry，2008，29（11）：1780.

［15］Wang X，Zheng H.Simulation of water potential for the electronic structure of serine［J］.Chinese Physics B，2009，18（5）：1968.

［16］Shen X，Gao Y，Zheng H.The equivalent dipole potential of water for the electronic structure of threonine［J］.Molecular Physics，2009，107（13）：1393.

［17］Gao Y，Shen X，Zheng H.Equivalent potential of water for electronic structure of asparagines［J］.International Journal of Quantum Chemistry，2010，110（4）：925.

［18］Min P，Zheng H.Equivalent potential of water for electronic structure of glycine［J］.Journal of Molecular Modeling，2010，17（1）：111.

［19］Wang X，Zheng H.A computer simulation of the electronic structure of leucine in aqueous solution［J］.Journal of Solution Chemistry，2011，40（7）：1317.

［20］Hohenberg P，Kohn W.Inhomogeneous electron gas ［J］.Physical Review，1964，136（3B）：864.

［21］Kohn W，Sham L.Self-consistent equations including exchange and correlation effects［J］.Physical Review，1965，140（4A）：1133.

［22］von Barth U，Hedin L.A local exchange-correlation potential for the spin polarized case：I［J］.Journal of Physics C：Solid State Physics，1972，5（13）：1629.

［23］Rajagopal A K.Advance in chemical physics：volume 41［M］.New York：Wiley，1979.

［24］Chen H.Electronic structure of clusters：applications to high-Tc superconductors ［D］.Baton Rouge：Louisiana State University，1988.

［25］Zheng H.Self-consistent cluster-embedding calculation method and the electronic structure of NiO and CoO［D］.Baton Rouge：Louisiana State University，1993.

［26］Sample H，Felton R H.A new computational approach to Slater’s SCF-Xαequation ［J］.Journal of Chemical Physics，1975，62（3）：1122.

［27］Guillot B.A reappraisal of what we have learnt during three decades of computer simulations on water ［J］.Journal of Molecular Liquids，2002，101（1-3）：219.

［28］Rick S W.Simulations of ice and liquid water over a range of temperatures using the fluctuating charge model［J］.Journal of Chemical Physics，2001，114（5）：2276.

［29］Berendsen H J C，Postma J P M，van Gunsteren W F.Intermolecular forces［M］.Dordrecht：Reidel，1981.

［30］Robinson G W，Zhu S B，Singh S，et al.Water in biology，chemistry and physics：experimental overviews and computational methodologies ［M ］. Singapore： World Scientific，1996.