型钢混凝土结构施工过程时变效应计算

吕 佳，吴 杰，罗晓群，张其林

（同济大学 土木工程学院，上海 200092）

型钢混凝土（steel reinforced concrete，SRC）组合结构强度高、刚度大、地震作用下延性好、施工周期短，因此被广泛应用于高层、超高层、大跨度结构等重要建筑中.与传统钢构件以及钢管混凝土构件相比，SRC组合构件为型钢外包混凝土，具有更好的耐火性及耐久性.在我国北京、上海等地相继建成或在建超高层建筑中，有多栋建筑采用了SRC组合结构形式，如北京香格里拉饭店、上海环球金融中心、上海中心等［1-4］.

国内外学者进行的大量研究表明，大型结构全寿命周期的多个过程中，有较多的工程事故发生在施工过程中，如：1907年的加拿大魁北克桥在架设过程中由于悬臂端的杆件失稳而破坏［5］，2009年上海市闵行区一栋在建的13层住宅由于未考虑施工堆载而发生倒塌等.在型钢混凝土组合结构中，由于施工阶段存在结构时变和混凝土的材料时变，结构各构件实际受力性能与一次加载模拟差别较大，且《高层建筑混凝土结构技术规程》（JGJ3—2010）［6］明确规定计算竖向变形差异时宜考虑混凝土收缩、徐变、沉降及施工调整等因素的影响，因此需对型钢混凝土组合结构施工过程计算方法进行研究.目前混凝土结构徐变的分析方法主要有Dischinger的微分方程求解法、Bazant的代数方程求解法以及基于位移法的有限元分析法等，前两种方法本质上都属于力法，应用较少，本文采用有效模量法（AEMM）与有限元法相结合的求解方法［7-10］.

大多数商业软件采用生死单元及组合截面等方法计算组合结构，但在结构时变及材料时变下，较难解决组合构件两种材料的协同工作问题.本文提出采用子结构单元模型并引入主从约束方法对组合结构进行有限元建模，从而实现混凝土和型钢两种不同介质的近似连续传力.采用有效模量法与有限元法相结合的方法来考虑混凝土时变，从而程序化解决组合结构施工过程结构时变及材料时变等问题.基于子结构单元模型研发了高层型钢混凝土组合结构施工过程模拟软件（SRCCM），并将其应用于工程实际，取得了较好的效果.

1 组合构件子结构单元模型

对于一般分离式组合构件（如图1所示T型截面），将截面形心位置定义为主节点［11-12］，钢及混凝土构件形心定义为从节点，节点间建立主从约束方程，从而实现混凝土和型钢两种不同介质的近似连续传力，并根据弹性力学基本方程，连接在从节点上的单元构件可以用主节点描述为

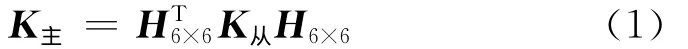
式中：K主为主单元刚度矩阵，K从为从单元刚度矩阵，H6×6为节点位移变换矩阵.图1表示的组合构件由混凝土构件和钢构件组成，因此组合构件的子结构单元刚度矩阵可表示为

当组合构件由m种材料组成，每种材料包含nj个子构件（j＝1，…，m）时，式（2）转化为

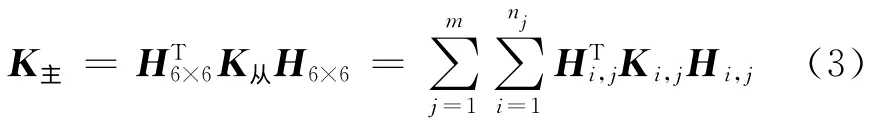
由式（3）来考虑钢及混凝土构件单元刚度矩阵对于总刚度的影响.当采用对称截面型钢混凝土组合构件时，其为一般分离式组合构件特例，此时混凝土构件与钢构件形心重合，主从节点位置重叠，计算方法同一般分离式组合构件.

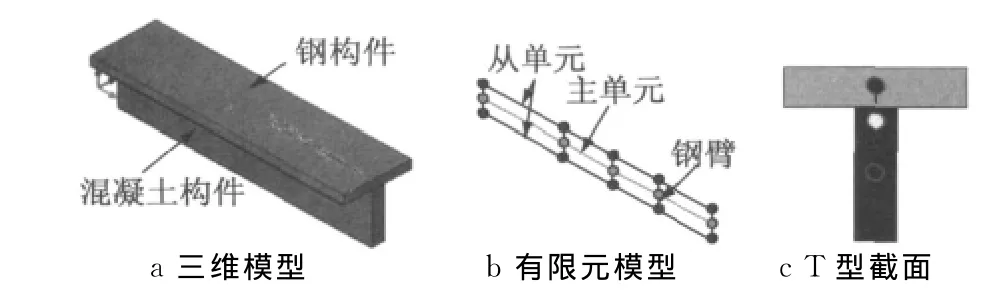
图1 主从节点计算模型Fig.1 Computation model of the master and slave nodes

2 型钢混凝土组合结构施工过程计算

2.1 型钢混凝土徐变计算模型

SRC在长期荷载作用下，组合构件材料处于弹性工作状态，且SRC构件内配钢筋，混凝土和钢材之间黏结可靠，因此可作如下假定［13-14］：

（1）型钢与混凝土之间有良好的黏结，满足变形协调条件.

（2）徐变变形与应力之间存在线性关系，服从Boltzman叠加原理.

（3）型钢混凝土截面平均应变满足平截面假定.

（4）混凝土部分平均曲率与型钢部分的平均曲率相同，即考虑混凝土与型钢共同变形.

基于上述假定对SRC轴压构件进行徐变效应受力分析，在轴力N作用下混凝土从时刻t0到t徐变应变为εc（t，t0），则由假定（4）可得构件的总应变为

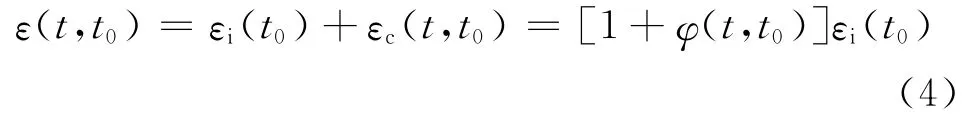
可得型钢承担的内力为

混凝土承担的内力为

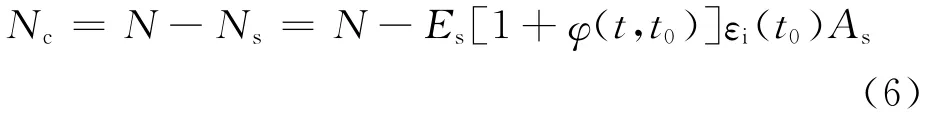
式中：εi（t0）为t0时刻弹性应变，φ（t，t0）为徐变系数，Es为钢材弹性模量，As为钢材面积.

型钢及混凝土构件在徐变作用下将发生内力重分布，型钢承担的荷载将逐渐增大，混凝土承担的荷载将减小.为解决徐变效应下钢和混凝土的协同作用问题，本文引入主从约束方法构造组合构件子结构单元模型，并将其应用于高层型钢混凝土组合结构施工过程分析模拟软件.

2.2 徐变效应计算

在Boltzman叠加原理和线性徐变的假设条件下，任意时刻tn的徐变应变

式中：σ（ti）为ti时刻弹性应力，E为混凝土弹性模量，φ（tn，ti）为ti时刻加载、tn时刻的徐变系数，σc（ti）为ti时刻徐变应力，ρ为老化系数，Eφ为有效弹性模量.依据位移法的有限元增量法，可得

式中：σi为ti时刻弹性应力增量，σ＊为徐变应力增量.根据Castigliano第一定理有

式中：F为徐变引起的杆端力，U为结构的徐变应变能，δ为徐变位移，γ（t，τ0）为混凝土有效弹性模量与实际弹性模量的比值，F0为初始弹性杆端力.上式表明由徐变引起的杆端力F由两部分组成：第一部分为由徐变位移δ产生的杆端力，第二部分为初始弹性杆端力F0引起的徐变所产生的相应杆端力.整理后可得到t＝t0到t＝tn-1的初始结构内力产生的第n阶段（tn-1→tn）的徐变位移

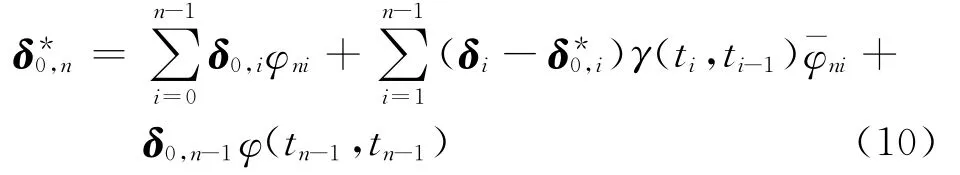
因此SRC组合构件混凝土材料徐变的计算可以先通过式（10）计算得到初始结构内力产生的徐变变形，然后引入边界条件通过式（9）计算得到徐变位移δ.

3 基于组合构件时变模型的软件研发

3.1 软件开发

基于主从约束法的组合构件子结构单元模型及混凝土时变效应计算方法，以AutoCAD为开发平台，运用ObjectARX和Visual C＋＋等开发工具，研发了型钢混凝土组合结构施工过程分析软件（SRCCM），可实现施工过程数据的交互式输入、计算结果的云图表现和文本结果的快速查询等功能.图2为软件架构图及软件主界面.

SRC组合结构施工过程计算需考虑结构时变及混凝土材料时变，通过赋予弹性模量初始值来激活各施工步骤相应构件，从而解决结构时变计算问题.混凝土材料时变程序设计流程见图3，其中K徐主为主单元徐变刚度矩阵，K徐从为从单元徐变刚度矩阵，N为施工阶段数.由图3可知，徐变分析以初始结构内力为基础，结构约束反力及外荷载随时间而变化，通过将各单元由徐变引起的单元杆端力进行叠加并引入边界条件来求解得到徐变引起的杆端位移，并得到徐变引起的约束反力及杆端力，从而解决混凝土时变计算问题.

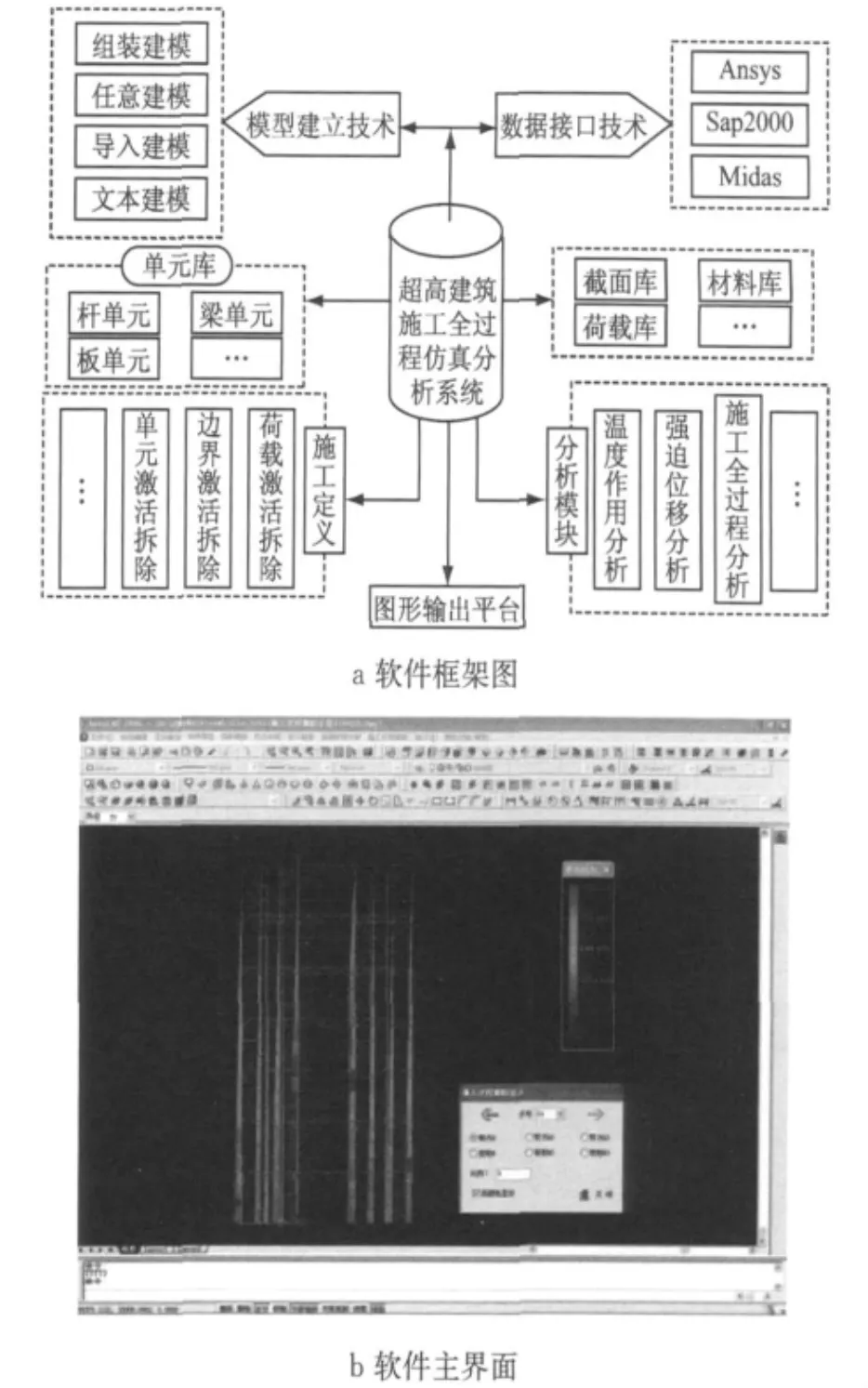
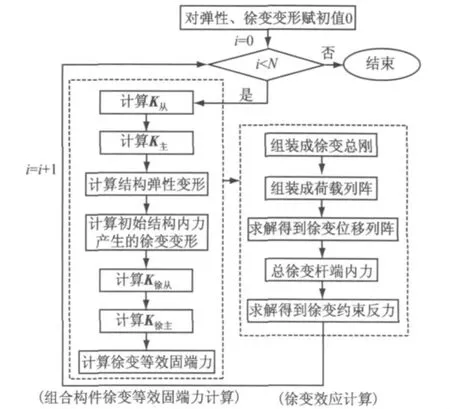
图3 程序设计流程图Fig.3 Program design flow chart

3.2 软件对比验证

图4为十二层型钢混凝土平面框架，其中A，B，C为柱轴线编号.框架柱截面尺寸为800mm×800mm，混凝土材料为C40，框架柱内包型钢及框架梁钢材都采用强度等级为Q345、截面尺寸为500mm×500mm×35mm×35mm的焊接工字钢.该施工过程分析共分为13个施工阶段（CS1～CS13），除CS13（100d）外其余12个阶段持续时间都为25d，每层梁单元上均布线荷载为10kN·m-1，平面框架施工过程计算模型如图4所示.

图4 平面框架施工过程分析Fig.4 Construction process analysis of plane frame

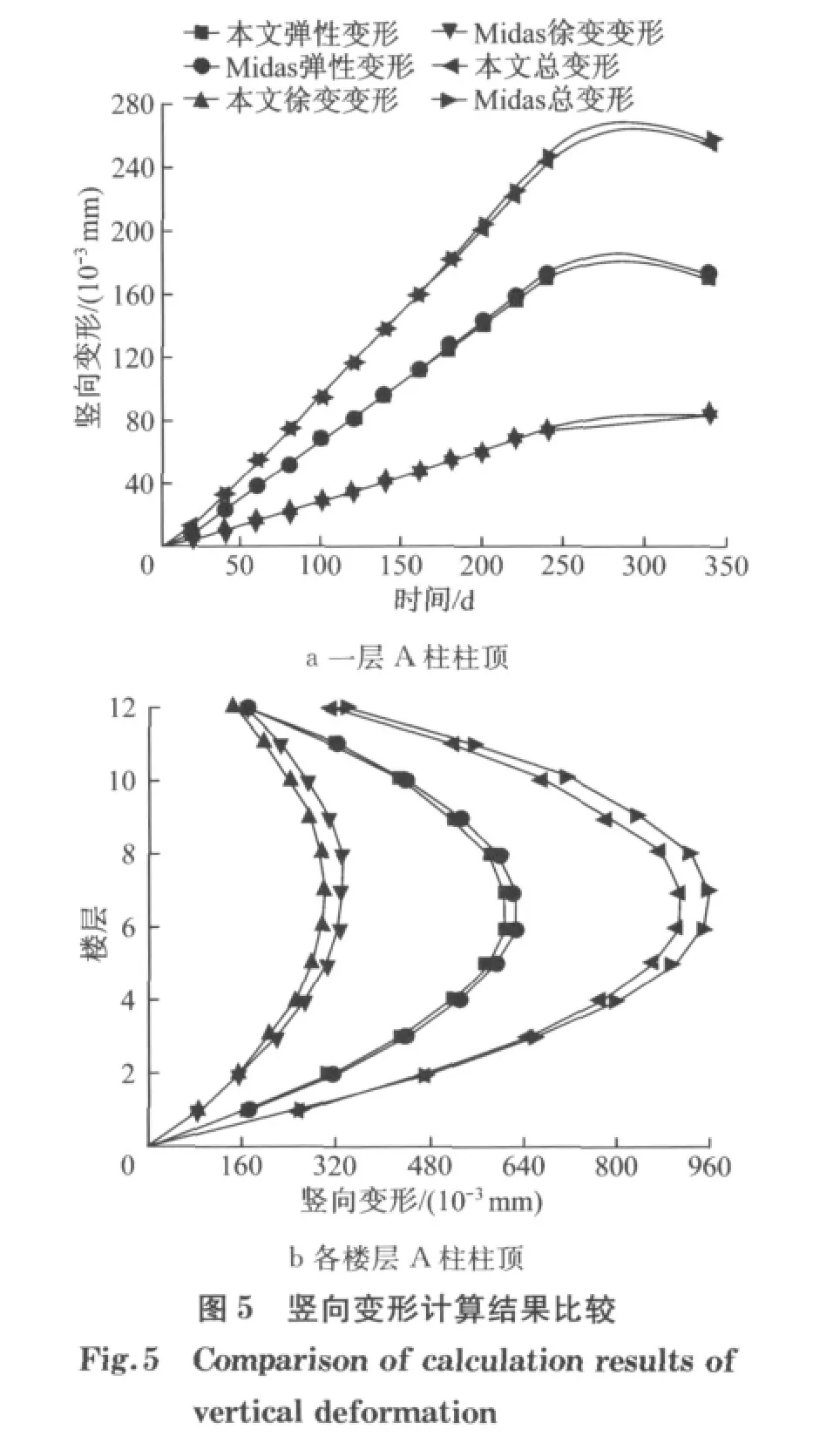
为了验证本文提出的基于主从约束方法的组合构件子结构单元模型的正确性，将计算结果与通用有限元软件Midas作了对比研究，Midas采用双单元分别模拟构件中钢和混凝土部分.施工过程计算结果如图5所示.从图5可以看出，本文与Midas计算结果基本一致，较小的差别在于徐变计算方法的不同，Midas徐变计算方法采用分时步徐变叠加法（SSM），而本文采用龄期调整有效模量法，故验证了该计算软件的正确性.

4 工程实例分析

4.1 计算模型

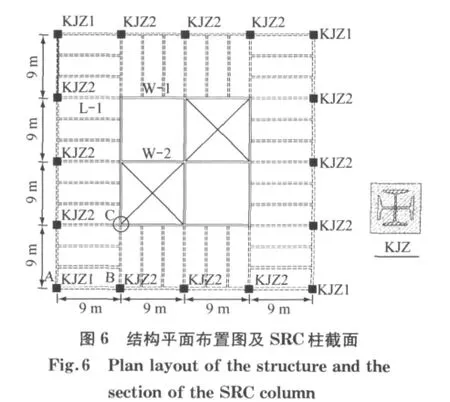
基于主从约束方法的组合构件子结构单元模型和施工过程时变计算理论，本文对某48层型钢混凝土框架-钢筋混凝土核心筒结构进行施工过程分析.结构层高3.6m，SRC柱钢构件采用形截面形式，框架梁采用焊接工字钢，钢材均采用Q345，核心筒混凝土及SRC框架柱混凝土按楼层所在标高分别采用C50，C40，C30混凝土材料.模型外围框架梁柱采用刚接，楼面梁与核心筒采用铰接，与框架采用刚接，结构平面布置见图6［15］，其中 KJZ为框架柱，L为梁，W为墙，A，B为柱子编号，C为墙编号.

4.2 施工过程模拟及分析

施工阶段模拟采用分层逐步施工方式，核心筒施工进度领先框架3层，为释放筒体及框架变形，混凝土楼板落后框架3层浇筑，施工进度为5d／层，假定3层为一施工段，结构封顶时共需18个施工段（CS1～CS18），为了研究长期荷载下影响，本文将研究结构封顶后1年、5年的变形及受力情况（CS19～CS20），共计20个施工段.

4.2.1 结构总变形

选柱A及墙C来研究SRC框架柱及核心筒的竖向变形，结构封顶5年后计算结果见图7.

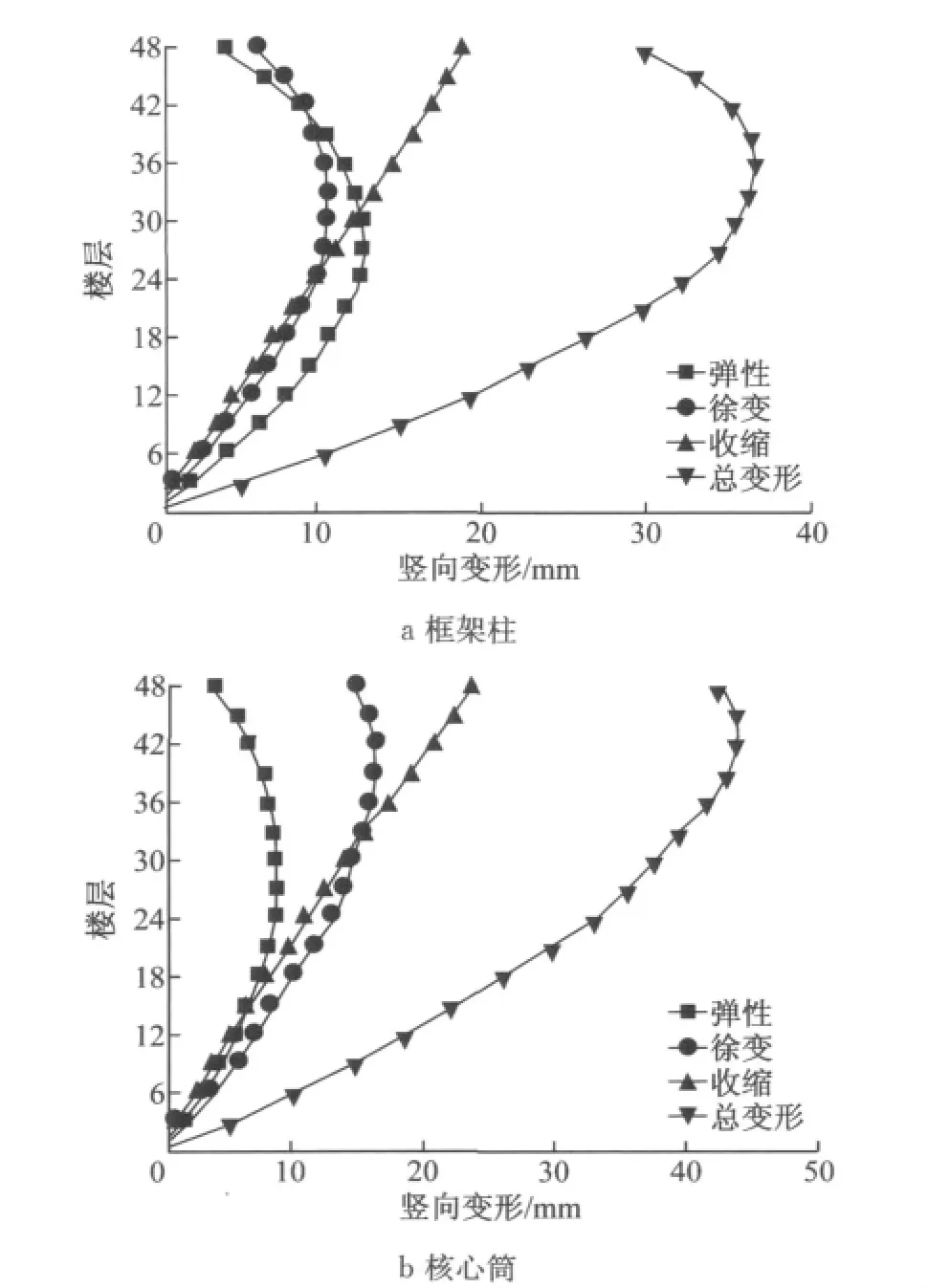
图7 结构封顶5年后结构竖向变形Fig.7 Vertical deformation over the past 5years after the completion of the top of the structure

由图7可见，SRC框架柱及核心筒弹性变形均随楼层升高而增大，且由于混凝土收缩徐变的影响，框架柱及核心筒竖向总变形最大值位置并不在顶层，框架柱的竖向总变形最大值位于36层，核心筒的竖向总变形最大值位于42层，框架柱变形值（36.66mm）小于核心筒变形值（43.91mm）.采用组合构件子结构单元模型模拟SRC构件施工过程竖向变形，可为实际施工提供找平依据，确保楼层实际标高与设计标高一致.

4.2.2 竖向变形差

柱B及剪力墙C封顶5年后考虑一次加载、结构时变、材料时变及施工过程的竖向变形差，计算结果见图8.

图8 结构竖向变形差Fig.8 Vertical deformation difference of the structure

在考虑核心筒提前3层施工的前提下，一次加载时框架柱与核心筒的竖向变形差最大且随层递增，在48层时竖向变形差达到13.29mm；只考虑混凝土收缩徐变时，核心筒竖向变形大于框架柱竖向变形且随层递增；只考虑结构时变时，框架柱与核心筒竖向变形差在27层达到最大值7.9mm，且各层框架柱变形均大于核心筒；考虑施工过程的变形差变化规律类似于只考虑结构时变，框架柱与核心筒的变形差在21层达到最大值，且42层以上楼层核心筒的变形反而大于框架柱.采用组合构件子结构单元模型模拟方法，可以得出型钢混凝土组合结构施工过程竖向变形差的变化规律，并可得出由此产生的水平构件内力变化，从而为设计和施工提供参考.

4.2.3 型钢和混凝土构件内力重分布

在自重及收缩徐变工况下，对采用组合构件子结构单元模拟的型钢及混凝土构件的轴力变化进行研究，对由结构时变、材料时变引起的型钢和混凝土内力重分布进行分析，其中柱A底部型钢及混凝土所受轴力随施工过程变化如图9所示.

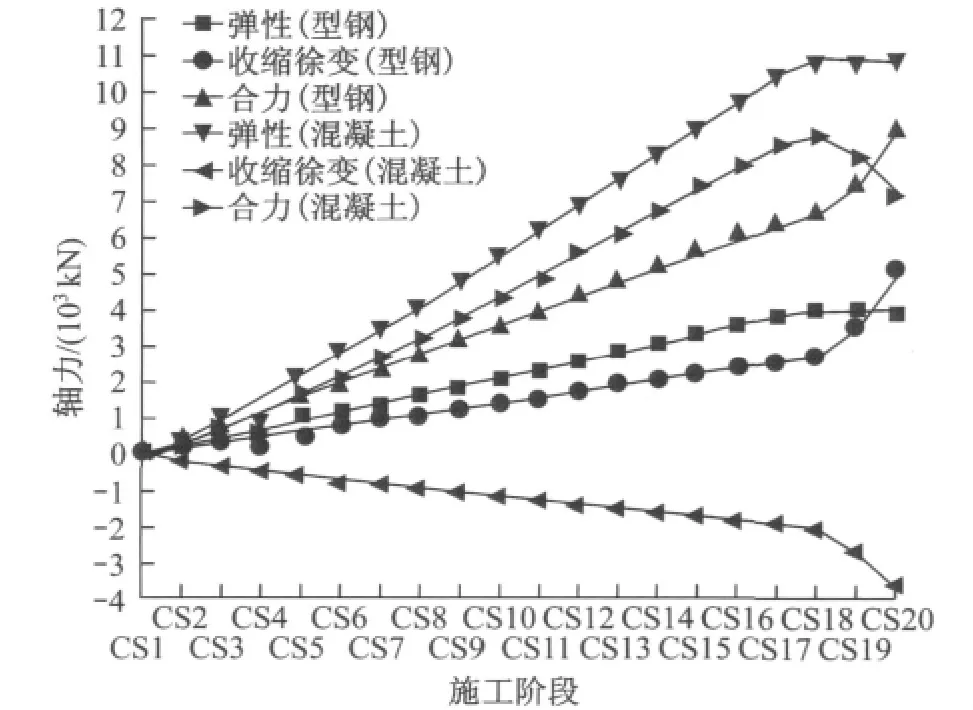
图9 不同施工阶段型钢和混凝土轴力变化图Fig.9 The axial forces change chart of steel and concrete at different construction stages

由图9可得，在前20个施工阶段，型钢和混凝土在自重及收缩徐变工况下所受的轴力合力都为压力，收缩徐变引起的混凝土轴力为拉力，且随时间而增大；在结构封顶前（CS1～CS18），型钢和混凝土轴力合力在结构时变及材料时变下随施工进度而增大，混凝土所受轴力合力略大于型钢所受轴力合力；在结构封顶时（CS18），混凝土轴力合力随着结构时变的结束而达到最大值8817.86kN，柱A所受轴力为15472.76kN；结构封顶后5年时间内（CS19～CS20），在材料时变下，混凝土所受轴力合力减小，型钢承担轴力合力将逐渐增大，符合式（5）和（6）计算方法，并由于梁柱的内力重分布，此时柱A所受轴力（16168.59kN）大于结构封顶时所受轴力合力.

5 结论

（1）基于主从约束方法的型钢混凝土组合构件子结构单元模型能够合理地反映组合构件的实际受力机制，较好地解决了组合构件中混凝土部分收缩徐变的计算问题，能够应用于型钢混凝土结构施工过程的时变分析.

（2）高层型钢混凝土组合结构必须考虑结构时变及材料时变对构件内力及结构变形产生的影响.

（3）研发的型钢混凝土组合结构施工过程模拟软件可以应用于高层组合结构施工过程的模拟分析，计算结果可为设计和施工提供参考.

［1］Ellobody E，Young B.Numerical simulation of concrete encased steel composite columns［J］.Journal of Constructional Steel Research，2011，67（2）：211.

［2］Dundar C，Tokgoz S，Tanrikulu A K，et al.Behavior of reinforced and concrete-encased composite columns subjected to biaxial bending and axial load［J］.Building and Environment，2008，43（3）：1109.

［3］Tokgoz S，Dundar C.Experimental tests on biaxially loaded concrete-encased composite columns［J］.Steel and Composite Structures，2008，8（5）：423.

［4］董建菲，魏巍，辛欣.型钢混凝土结构的研究发展及应用［J］.陕西建筑，2009（2）：5.DONG Jianfei，WEI Wei，XIN Xin.Research development and application of steel reinforced concrete structure［J］.Shaanxi Architecture，2009（2）：5.

［5］陈绍蕃.钢结构设计原理［M］.北京：科学技术出版社，1998.CHEN Shaofan.Principles of steel structure design ［M］.Beijing：Science ＆Technology Press，1998.

［6］中华人民共和国建设部.JGJ3—2010高层建筑混凝土结构技术规程 ［S］.北京：中国建筑工业出版社，2011.Ministry of Construction of P R China.JGJ3—2010 Technical specification for concrete structures of tall building ［S］.Beijing：China Architecture and Building Press，2011.

［7］Dischinger F.Investigation of the buckling resistance，the elastic deformation and the creep of the concrete in arch bridges［J］.Civil Engineering，1937，18（33／34）：487.

［8］Bazant Z P.Prediction of concrete creep effects using ageadjusted effective modulus method［J］.ACI Journal，1972，69：212.

［9］Mazzotti C，Savoia M.Experimental study of nonlinear creep of concrete at high stress level［J］.ACI Structural Journal，2006，103（2）：259.

［10］肖汝诚.桥梁结构分析及程序系统［M］.北京：人民交通出版社，2002.XIAO Rucheng.The structure analysis and program system of bridge［M］.Beijing：China Communications Press，2002.

［11］王勖成.有限单元法［M］.北京：清华大学出版社，2010.WANG Xucheng.Finite element method ［M］.Beijing：Tsinghua University Press，2010.

［12］Giakoumelis G，Lam D.Axial capacity of circular concretefilled tube columns ［J］.Journal of Constructional Steel Research，2004，60（7）：1049.

［13］孙海林，叶列平，丁建彤.混凝土徐变计算分析方法［C］／／赵铁军.高强与高性能混凝土及其应用：第五届学术讨论会论文集.青岛：中国建筑工业出版社，2004：180-186.SUN Hailin，YE Lieping，DING Jiantong.The method of concrete creep calculation［C］／／ZHAO Tiejun.Concrete of High Strength and High Performance and Its Application：Proceedings of the Fifth Seminar.Qingdao：China Architecture and Building Press，2004：180-186.

［14］赵世春.型钢混凝土组合结构计算原理［M］.成都：西南交通大学出版社，2004.ZHAO Shichun.Calculation principle of steel reinforced concrete structure ［M］.Chengdu：Southwest Jiaotong University Press，2004.

［15］周绪红，黄湘湘，王毅红，等.钢框架-钢筋混凝土核心筒体系竖向变形差异的计算［J］.建筑结构学报，2005，26（2）：66.ZHOU Xuhong，HUANG Xiangxiang，WANG Yihong，et al.Calculation of the differential shortening of steel framereinforced concrete core wall structure［J］.Journal of Building Structures，2005，26（2）：66.