利用曲线系巧解几何题

●

(宁波市第二中学 浙江宁波 315000)

利用曲线系巧解几何题

●罗树锋

(宁波市第二中学 浙江宁波 315000)

双直线、双切线方程虽在高中课本里没有出现过，但是与它们相关的题目却层出不穷，一般在解决这类问题时习惯用韦达定理“设而不求”的方法.毋庸置疑，韦达定理在解决直线与二次曲线的问题时有着强大的作用，但繁杂的运算却使我们望而却步.下面介绍利用双直线、双切线方程(2个在曲线系里具有举足轻重的方程)巧解解析几何中的一类问题.

首先给出双直线方程、相交曲线系方程、双切线方程的概念：

双直线方程如果有2条直线A1x+B1y+C1=0，A2x+B2y+C2=0,则方程(A1x+B1y+C1)(A2x+B2y+C2)=0称作这2条直线的双直线方程，它将2条直线统一为一个二次曲线.

相交曲线系方程如果有2条相交曲线F(x,y)=0,G(x,y)=0，则F(x,y)+λG(x,y)=0表示过2条曲线F(x,y)=0,G(x,y)=0交点的曲线方程(不包括G(x,y)=0这条曲线).

由双直线方程和相交曲线系方程进一步可以得出双直线方程的另一种表示形式：设二次曲线Ax2+Bxy+Cy2+Dx+Ey+F=0，P(x0,y0)是曲线上的一点，则过点P(x0,y0)的切线方程为

设曲线上异于点P的2个点A,B的直线方程为A′x+B′y+C′=0，则直线PA,PB的双直线方程为

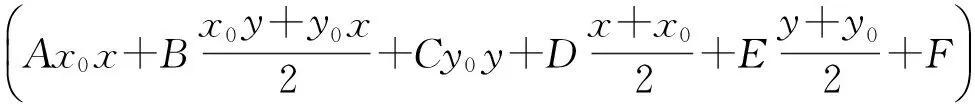
双切线方程从二次曲线外一点引曲线的2条切线，称为该点关于该曲线的双切线，把切点弦看成是2条重合直线，则双切线就是过该双重合直线与二次曲线公共点的相交双直线，可表示为

将P(x0,y0)代入可得双切线方程.

下面举例说明上述方程的应用：

例1直线x-2y-1=0与抛物线y2=4x交于点A,B，点C在抛物线上，∠ACB=90°，则点C的坐标为______.

(2011年全国高中数学联赛一试试题)

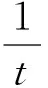
比较式(1)，式(2)的系数：由于x2项的系数相等，则各项系数相等；由y2项的系数相等得

(5)

由式(3)～式(5)得t=-1或t=-3，因此点C坐标为(1,-2)，(9,-6).

例2如图1,已知抛物线C1:x2=y，圆C2:x2+(y-4)2=1的圆心为点M.

(1)求点M到抛物线C1的准线的距离.

(2)已知P是抛物线C1上一点(异于原点)，过点P作圆的2条切线交抛物线C1于点A,B.若过点M,P的直线l垂直于AB，求直线l的方程.

(2011年浙江省数学高考理科试题)

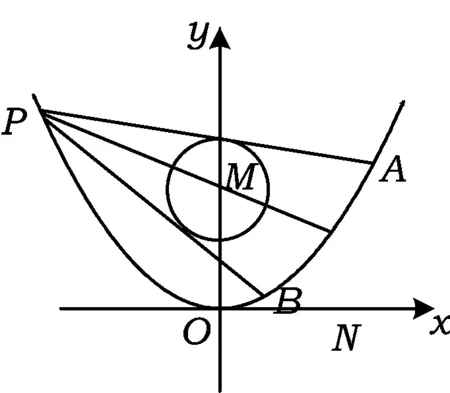
图1

解(1)略.

(2)设点P的坐标为(t,t2)，则过点P的抛物线的切线方程为

y-2tx+t2=0.

又圆关于点P的切点弦方程为xt+(y-4)(t2-4)-1=0，从而圆的双切线方程为

又点P满足式(7),代入得

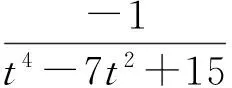
从而圆的双直线方程为

比较式(6)与式(8)y2项的系数与xy项的系数，得

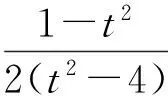
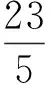
图2

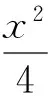
(1)当直线PA平分线段MN，求k的值；

(2)当k=2时，求点P到直线AB的距离；

(3)对任意k>0，求证：PA⊥PB.

(2011年江苏省数学高考理科试题)

解(1)(2)略.

(3)设P(x0,y0)，则由图形的对称性和题意易知点A和点C的坐标分别为(-x0,-y0)和(x0,0).设直线PA斜率为k1，直线PB斜率为k2，则直线PA,PB的双直线方程为

(y-k1x)[y-y0-k2(x-x0)]=0,

即 (y-k1x)(y-k2x+k2x0-y0)=0.

(9)

比较式(9)，式(10)中的常数项得λ=-y0，再比较x2项与y2项的系数得k1k2=-1，即PA⊥PB.

上述例题给出的参考答案更多地是利用韦达定理，但运算中分式较多且较为复杂，容易出错.利用双直线和双切线方程，问题就集中到了同一个曲线的2种不同表达形式的系数对应关系，而系数对应关系有着直观简洁的特点，里面的参数λ,μ可以利用已知条件求解，也可以“设而不求”，降低了运算的难度，能够更快、更好地解决问题.

[1] 胡圣团.二次曲线中点弦、切线、切点弦及双切线方程[J].中等数学,2008(9):7-11.