巧用课堂中的典型错误提升课堂效率的若干策略
2013-10-26
●
(东北师范大学南湖实验学校 浙江嘉兴 314000)
巧用课堂中的典型错误提升课堂效率的若干策略
●周立志
(东北师范大学南湖实验学校 浙江嘉兴 314000)
在课堂教学中,经常会出现大量的学习错误:对解法混淆运用;对结论掌握不全;对概念理解不透;……其中许多错误真实记录了学生数学思维的过程.教师若能随机应变,巧妙地利用这些“错误”,变废为宝,则可以帮助学生从错误中走出来,同时引导学生进行自我反思与归类,有效提高课堂的教学效率和学生的学习能力.本文结合笔者的日常教学加以阐述.
1 将错就错——让错误彰显精彩
当代科学家波普尔说:“错误中往往孕育着比正确更丰富的发现和创造因素.”学生在数学学习中出现错误是不可避免的,同时课堂上发生的错误也并非一文不值:它往往能暴露出学生的真实想法,反映出学生的思维能力,包含着有价值的成分.教师若能善于发现错误背后隐藏的合理价值,巧用错误,则能让课堂妙趣横生,充满生成.
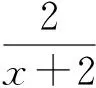
笔者在巡视时发现,犯错误的学生不是个别.这时候,做对了的学生在下面哄笑,那个出错的学生一脸尴尬.笔者当场来个“顺水推舟,将错就错”:“刚才去分母的这位同学的解法显然是错的,可我发现出错的并非就此一人.有一部分同学也把分式的化简当作分式方程来解了,解法虽然错了,但也有这种方法的优点,那就是去掉分母来解,其解法简捷明快,因此我们考虑能否利用方程来解呢?”整个班级顿时陷入了思考,成绩较好的学生探究的声音也很轻,显得比较谨慎.显然,学生们被难住了.笔者再及时跟进,予以提醒:“刚才‘当作’分式方程解是错的,注意现在我说是‘利用’分式方程来解.”过了几分钟,有学生兴奋地站起来:设这个分式等于一个字母.于是一个“另类”的解题过程就呈现了.
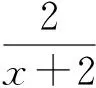
2(x-2)-2(x+2)=A(x+2)(x-2),
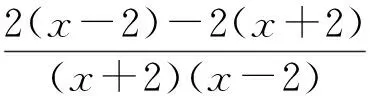
于是大家感觉用方程解法化简分式的方法有创意,更重要的是这种“将错就错”得到的结果也让刚才做错的学生体面地化解了尴尬.
可见,教师要充分利用学生学习中出现的错误,鼓励学生从多角度、全方位审视自己在学习活动中出现的错误,因势利导.这种教学的效果远远胜于直接告诉学生一个正确的结论.
2 巧设陷阱——让错误激发反思
英国心理学家贝恩布里奇说:“错误人皆有之,作为教师不利用是不可原谅的.”因此,教师可以有意识地选择一些学生极易出错的题目,设置“陷阱”,让学生陷入歧途,产生思维冲突,从中可以诱导出学生在认知中的错误或片面观点,有助于教师及时捕捉、弄清教学对象的认知特点,采取有效的教学措施,使教学具有针对性.
案例2反比例函数中的增减性一方面与一次函数有着相反的性质,另一方面增减性是不连续的,运用该知识点解题时学生极易出错.笔者在期末总复习时就碰到一例.浙教版《数学》9年级上册作业本(2)第32页习题如下:
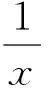
( )
A.y1
D.y1与y2之间的大小关系不能确定
学生解答时几乎都选A,理由很“充分”:k=-1,y随x的增大而增大.对于这样的局面,笔者没有急于给出正确结论,而是引导学生回顾已学知识:
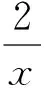
学生一一回答,其中笔者特意将增减性这一性质写成2行:
当k>0时,y的值随x的增大而减小.
接着,笔者有意识地设计了以下一组问题,让学生“陷入歧途”:
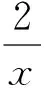
由于有了前面学习反比例函数的经验,学生马上回答:y1>y2.
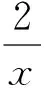
学生异口同声回答:y1 学生很响亮地回答:y1 “误导”很成功! 学生依旧响亮回答:y1>y2! 这时,笔者注意到平时善于思考的学生M面露困惑,她站起来讲述了想法,学生们都傻眼了:当x1=-1时,y1=-2;当x2=1时,y2=2,此时y1 教室马上由热闹陷入沉思.不久,有学生顿悟:“老师,我们忽略了‘在每一象限内’这句话.”笔者马上用彩笔在先前故意分段留有空白的地方补上:在每一象限内.至此,学生对错题中的错因心知肚明,错误不教而解. 美国数学家波利亚说过:“错误中往往孕育着比正确更丰富的发现和创造因素,发现的方法就是试错的方法.”该案例的教学中如果只是机械地告诉学生不要忽略“在每一象限内”这一条件,那学生就只能在教师的“谆谆告诫”下僵化、被动地接受知识,其结果是将会成为技能低下、缺乏质疑精神和探索精神的书呆子.因此,教师在错误分析的过程中不必担心学生犯错,而应该尽可能把学生头脑中的问题“挤”出来,把思考问题的思维缺陷暴露出来,以此来激发学生重新反思错误,进而达到纠错的目的. 布鲁纳说:“学生的错误都是有价值的.”学生在解题时出错的原因是多样的,教师应立足学生,从多样的错误中去发现学生思维的漏洞、误区,顺势而上,顺藤摸瓜,引导学生找到错误根源,让学生在错误中寻求到正确的方向,促使学生的思维水平有层次、有步骤地向更优化的方向发展. 案例3学生在运用三角函数定义解题时,容易受到定义学习过程中构造直角三角形的影响,得到错误结论.笔者在一次作业讲评课中就碰到一例: 图1 (该学生的回答马上赢得了部分学生的“认可”.) 师:哦.那我们是不是可以认为如果不是直角三角形,锐角就没有三角函数值呢? 教室突然静了下来,刚才“认可”的学生也开始打开书本. 生2(激动地):不对,不是直角三角形的锐角也有三角函数值,比如教材第12页作业题有很多锐角就有三角函数值. 生3:而且我发现书本上的定义告诉我们只有用边去求三角形函数值时才需要在直角三角形中. 生3(自信地):仅仅得到∠B=30°而已,其他的角是多少度不能得到. 因为学生对锐角三角函数概念的本质掌握不到位,造成思维定势,进而得出直角三角形的结论.可见,当学生暴露错误苗头时,教师不要急于给出正确的结论与过程,而应通过对学生的错误展开刨根究底的追问,引导学生去发现、纠正,从而使学生的知识主动建构,形成了正确而完整的知识体系. 杜威曾说过:“失败是有教导性的,真正懂得思考的人,从失败和成功中学得一样多!”因此,教师除了将学生中的错误做典型分析外,还应该引导学生善于将平时解题所犯的错误进行收集归类与反思.比如,教师可以要求班级每个学生准备一本《数学纠错本》,专门记录平时做错的题以及错误的过程,指导学生将解错原因化归为概念出错还是计算、应用出错,并在错题后附上自己做错的原因.而对于相同类型的错题,则引导学生删选出最典型的错题,订正出正确的过程.这种纠错的方式,让学生在自我分析的反思过程中加深了对薄弱知识的理解与掌握. 此外,教师在每一章节结束后,利用1~2个课时在班级进行纠错与反思心得交流活动,在活动中展示出最深刻的反思或最典型的错误类型,起到借鉴、共勉的效果. 案例4学生F在一次交流中讲道: 这样幽默地讲述,留给学生们的印象是极其深刻的.这样的活动激发了学生进行错题摘录的兴趣,同时也潜移默化地让学生养成“平时有空翻一翻、考前认真看一看”的习惯,从而达到错一次而收获十倍的效果. 所谓错误,是指师生在认知过程中的偏差或失误,错误伴随着教学的始终,而且错误是无法避免的.教师在遇到错误时,应针对不同原因,变废为宝,巧用这一生成的宝贵教学资源辅助课堂教学,帮助学生灵活纠错,努力让错误成为数学课堂教学的一个亮点,成为重要的课程资源,让其闪现创新的火花,发挥应有的价值. (注:本文为2012年度教育部人文社科一般级项目“智慧型学校的实践研究与理论分析——依托大学与中小学合作的学校改进的行动研究”(编号:12YJA880057)的研究成果之一.) [1] 教育部.义务教育数学课程标准:2011版[M].北京:北京师范大学出版社,2012:8. [2] 李建新.让错误成为教学的亮点[J].教育革新,2011(11):17-18. [3] 吴刚妹.暴露错误成就精彩课堂[J].新课程研究:上旬刊,2012(5):13-14. [4] 陈锐.树立正确的学生错误观——以教学中的错误为例[J].考试周刊,2012(30):20-21.
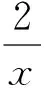
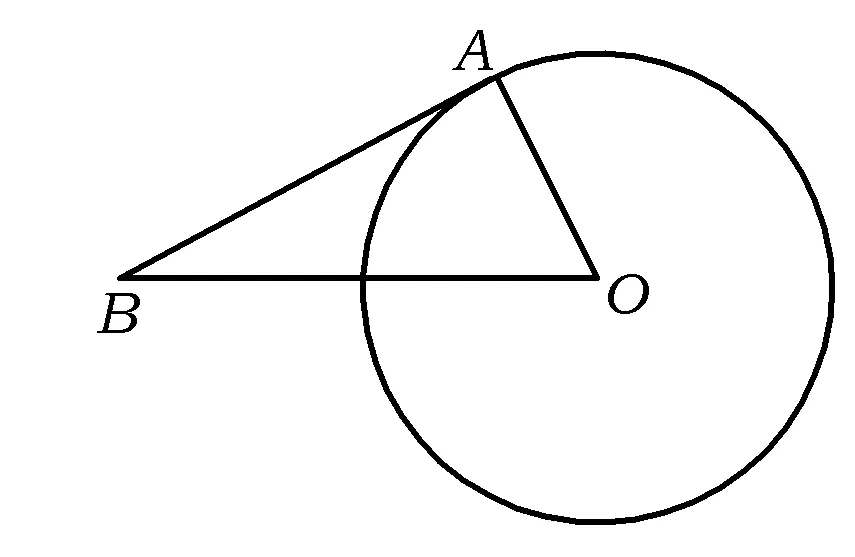
3 顺藤摸瓜——让错误无处遁形
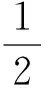
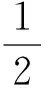
4 反思归类——让错误渐行渐远
