一道湖北预赛试题的解法及一般性结论

●

(会宫中学 安徽枞阳 246740)

一道湖北预赛试题的解法及一般性结论

●王怀明汪根友

(会宫中学 安徽枞阳 246740)

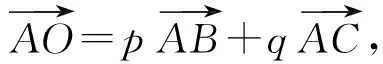
(2012年全国高中数学联赛湖北省预赛试题)

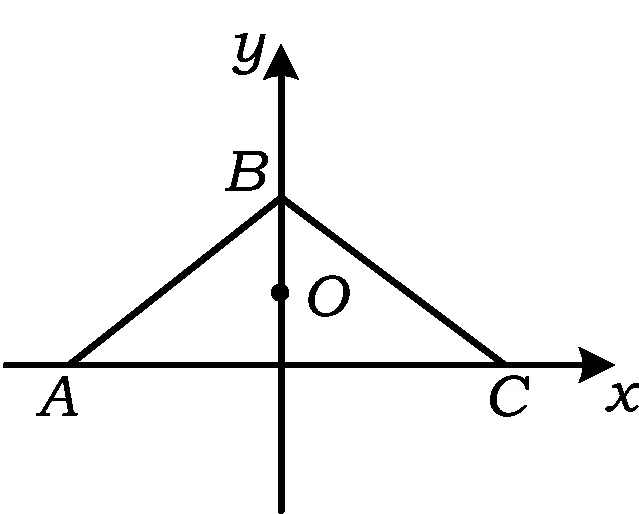
图1

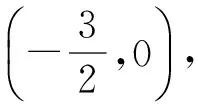
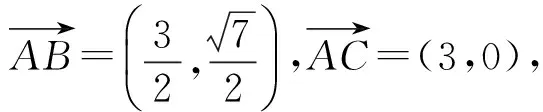
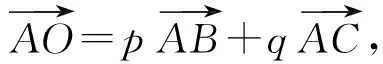
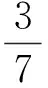
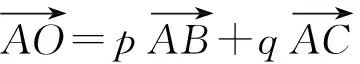
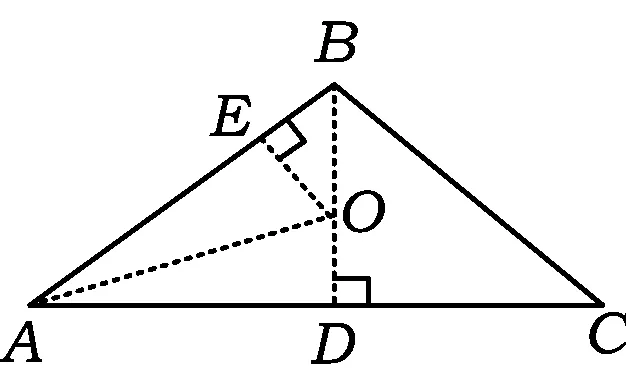
图2

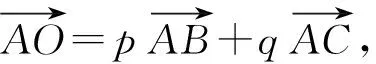
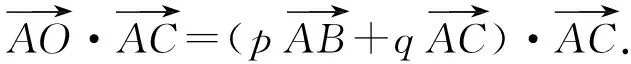
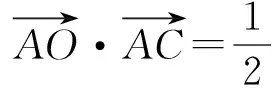
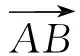
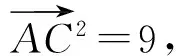
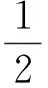
(1)

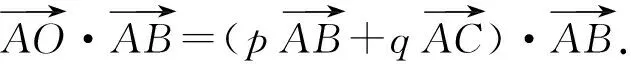
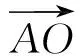
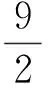
(2)

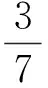
评注该解法通过构造数量积,把向量等式化为数量形式,然后利用向量数量积的几何意义,通过计算得到2个方程,计算量比解法1要小.

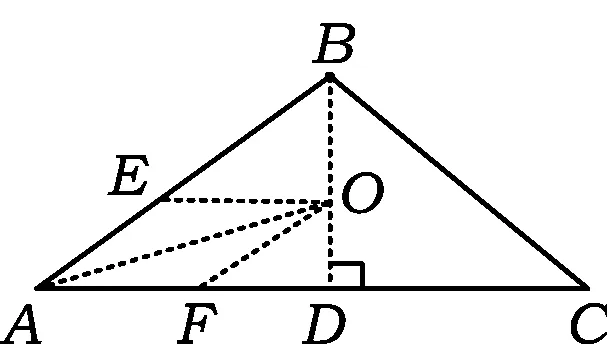
图3

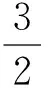
AF=OF=AE.

由OF∥AB,得

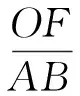
即

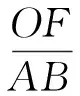
解得

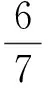
因此

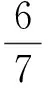
因为AB=2,AC=3,所以

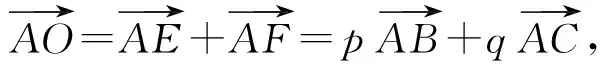
评注该解法根据平面向量基本定理作平行四边形,再由三角形内心的性质求出p,q的值,计算量较小.

我们发现p,q的值与△ABC的3条边的长度紧密相关:它们的分母7等于3条边长度之和,分子分别等于AB,AC的长度,p,q的比值恰好等于2条边AB,AC的长度之比,是巧合还是必然?经过探究,笔者得到如下结论:

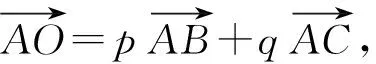
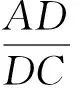
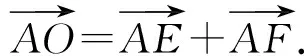
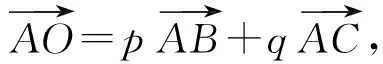
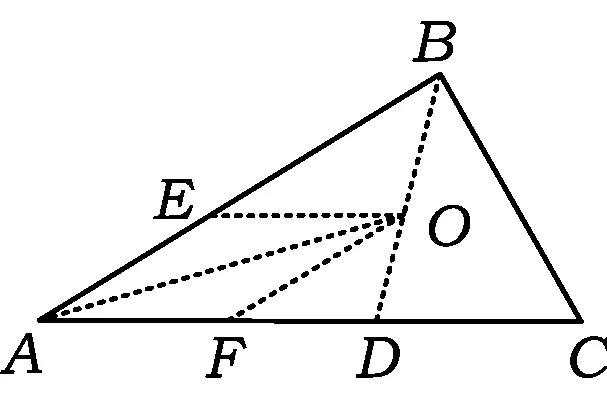
图4

由点O是△ABC的内心,得AO平分∠BAC,即四边形AEOF是菱形,从而

AE=AF=OF.

由OF∥AB，得

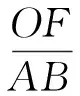
即

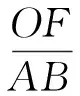
解得

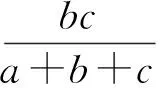
因此

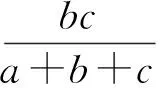
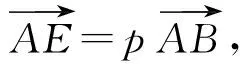
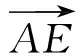
即

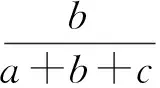
同理可得

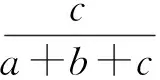
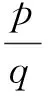
笔者还发现p,q的比值仅与边AB,AC的长度有关,而与另一边BC的长度无关,因此该试题的条件“BC=2”是多余的.若要求出p,q的值,则需要用到此条件.