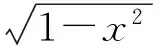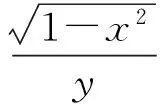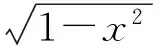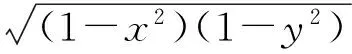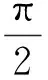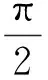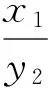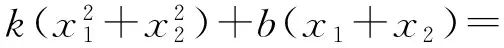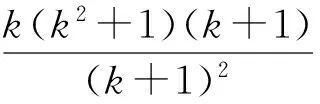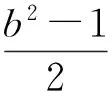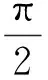学习增新知 题解又一春

●

(腾冲县第一中学 云南腾冲 679100)

学习增新知题解又一春

●罗仁幸

(腾冲县第一中学 云南腾冲 679100)

文献[1]中的例3题意如下：

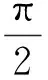
笔者试图从三角函数的内部知识和三角函数定义过渡到解析几何、代数式的恒等变形等3个方面进行思考，并提出自己的拙解，以拓宽解题思路，丰富题目内涵，挖掘数学思想方法，揭示其规律.不妥之处请批评指正.

cosαsinα+cosβsinβ=2sinαsinβ，

即

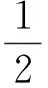
通过和差化积与积化和差，得

sin(α+β)cos(α-β)=cos(α-β)-cos(α+β),

即 cos(α+β)=cos(α-β)[1-sin(α+β)].

(1)

因为α,β为锐角，所以

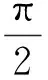
故

cos(α-β)>0,1>1-sin(α+β)≥0.

由式(1),得

cos(α+β)≥0，

从而

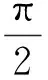
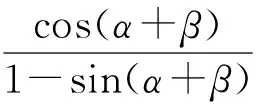
从而

cos(α+β)≤1-sin(α+β)，

即

cos(α+β)+sin(α+β)≤1(不成立)，

评注证法1主要运用三角函数知识证明.

证法2设x=sinα,y=sinβ.因为α,β为锐角，所以

0

即

两边平方，得

即

(x2+y2)2- (x2+y2)+2x2y2=

(2)

再两边平方，得

(x2+y2)4-2(x2+y2)3+(x2+y2)2+

4x2y2(x2+y2)2-4x2y2(x2+y2)+4x4y4=

4x2y2[1-(x2+y2)+x2y2],

化简整理，得

(x2+y2)2[(x2+y2)-1]2+4x2y2[(x2+y2)2-1]=0，

因式分解，得

[(x2+y2)-1] [(x2+y2)3-(x2+y2)2+

4x2y2(x2+y2)+4x2y2]=0,

因此

x2+y2-1=0

或(x2+y2)3-(x2+y2)2+4x2y2(x2+y2)+4x2y2=0.

由式(2),知

(x2+y2)2-(x2+y2)+2x2y2>0,

结合x2+y2>0,得

(x2+y2)3-(x2+y2)2+2x2y2(x2+y2)>0,

因此

(x2+y2)3-(x2+y2)2+4x2y2(x2+y2)+4x2y2=

[(x2+y2)3-(x2+y2)2+2x2y2(x2+y2)]+

[2x2y2(x2+y2)+4x2y2]>0,

从而

x2+y2=1,

即

sin2α+sin2β=1.

评注证法2换元后主要用代数式变形进行推证.

证法3如图1，设锐角α,β的终边与单位圆分别交于点A(x1,y1),B(x2,y2).由三角函数定义知

cosα=x1,sinα=y1,cosβ=x2,sinβ=y2.

图1

设过A，B的直线方程为y=kx+b.联立方程组

消元整理得一元二次方程

(1+k2)x2+2kbx+b2-1=0.

依条件，点A,B在第一象限，则

(3)

x1y1+x2y2=x1(kx1+b)+x2(kx2+b)=

2(kx1+b)(kx2+b)，

2[k2x1x2+kb(x1+x2)+b2],

即

即

k(2k2b2+2+2k2-2b2)=

(1+k2)(2kb2+2b2-2k2),

故k4+k3+k2+k=(k2+2k+1)b2.

(4)

k=-1.

此时

从而

cos(α+β)= cosαcosβ-sinαsinβ=

x1x2-y1y2=0.

因为α,β是锐角，所以

评注证法3运用三角函数定义、解析几何知识、一元二次方程等相关知识进行推证.

以上3种证法分别从不同的角度进行分析论证，论证中涉及的知识主体属数学中的不同内容，但殊途同归，最终使问题得以解决.作为数学思维方法训练，理解掌握数学知识无疑是很有意义的一件事；另一方面，“探求规律，实事求是”是数学的学科精神；其三，笔者受文献[1]的启示，得出本文中解法，给题目添加了新的解法，同时给笔者一个学习和实践解题的机会，真可谓“学习增新知，题解又一春”！

[1] 应之宁,纪斐.等与不等相互转化中不等的构建[J].中学教研(数学)，2012(2)：35-38.