保序变换半群到保序部分变换半群的同态
2013-10-24高京南杨秀良
高京南,杨秀良
(杭州师范大学理学院,杭州310036)
1 引言和预备知识
令Xn{1,2,…,n}.集合Xn上的所有保序变换在复合运算下构成的半群称为Xn的保序变换半群,记作On;Xn上的所有保序部分变换在复合运算下构成的半群称为Xn的保序部分变换半群,记作POn.它们的许多性质已经被前人研究[1-10].特别地,Fernandes等人在[1]中研究On的自同态,Lavers和Solomon在[2]中研究On的同余,杨浩波在[3]中研究POn的同余.在本文作者将进一步研究On和POn之间的同态.
作者所提到的映射是右映射.S,T为两个半群,φ∶S→T为映射.若对任意的x,y∈S,都有(x)φ(y)φ=(xy)φ,则称为 φ 为同态.由[4]知,On,POn均为正则半群.
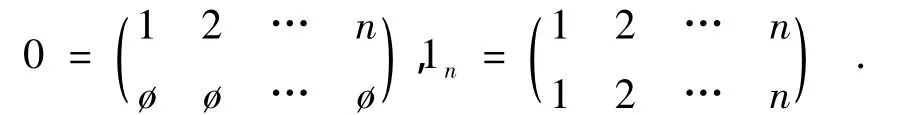
由[1],[5]知,On,POn上的格林关系都为:

2 主要结果
得到结果:
定理1 令φ∶On→POn为任一映射,φ是同态当且仅当φ是下面之一:
(1)对任意的 α∈On,都有(α)φ =α;
(2)对任意的 α∈On,有(α)φ =ασ,其中,ασ=σ-1ασ,
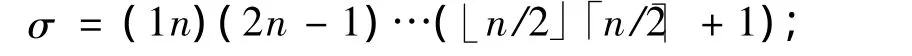
(3)存在幂等元 e,f∈E(POn),其中 e≠f且 ef=fe=f,有(1n)φ =e,(On/{1n})φ =f;
(4)选取 e∈E(POn),对任意的 α∈On,都有(α)φ =e;
(5)
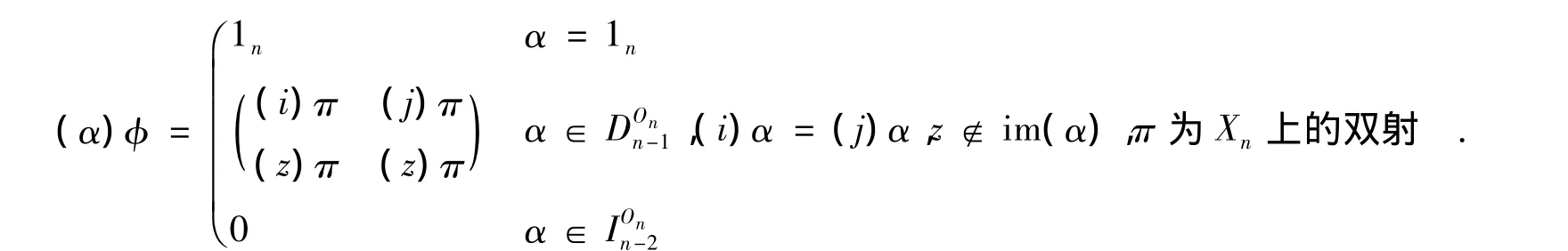
定理2 记H={φ∶φ为On到POn的同态},则
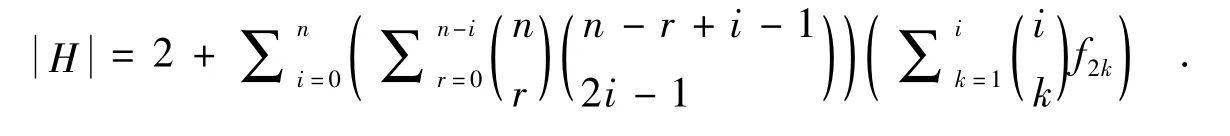
其中,f2k为第2k个斐波那契数.
3 定理1的证明
显然定理 1 中的(1),(2),(3),(4),(5)均为同态.故只需证明除了(1),(2),(3),(4),(5)外没有别的同态.
设 φ∶On→POn为同态,则 Kerφ ={(a,b)∈On×On∶(a)φ =(b)φ}为 On上的一同余.由[2]知,Kerφ 为 Rees同余.由[6]知,On的所有理想均有形式 IOnk={α∈On∶r(α)≤k},1≤k≤n,故存在 1≤k≤n,使:
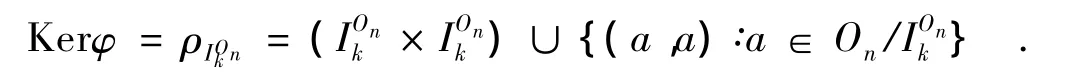
当k=n时,Kerφ为泛同余,此时,φ具有形式(4);当k=n-1时,Kerφ共有两个同余类,分别为IOnn-1,{1n},此时φ具有形式(3).由[2]知,On上的同余有Rees同余和恒等同余.当On上的同余为恒等同余时,由[7]知,φ 具有形式(1),(2).
当 k=n-2 时,IOnn-2为 Kerφ 的一个同余类,φ 在 On/IOnn-2上为单射.今(IOnn-2)φ =τ,其中,τ∈EIOnn-2,故可得
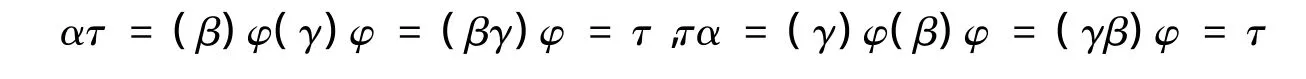
即ατ=τα=τ.
因同态保持D类,故DOnn-1在φ下的像应包含在POn的某个D类中,不妨设为DPOnx,其中,0≤x≤n.任取 α∈(GOnn-1)φ,则有 τα =τ 可知,im(f)⊆im(α),故 x≥i,假设 x=i,则有 im(f)=im(α).故 τ= α.(否则,存在 j∈X,使得(j)τ≠(j)α.因 im(τ)=im(α),则有(j)α∈i m(τ),故由 τ是幂等元可知,((j)α)τ=(j)α,而 ατ=τ,故(j)τ=(j)ατ=((j)α)τ=(j)α,矛盾).从而(GOnn-1)φ =τ,即 GOnn-1与 IOnn-2包含于Ker(φ)的同一个同余类中.这是不可能的,故假设不成立.从而x>i,也即(DOnn-1)φ⊆DPOnx,其中i<x≤n.
任取 δ≠σ∈(GOnn-1)φ,则有
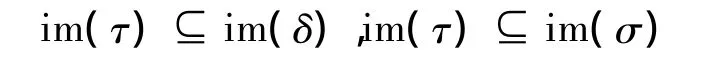
不妨令 Cδ=im(δ)im(τ),Cσim(σ)im(τ).则有
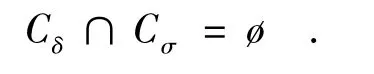
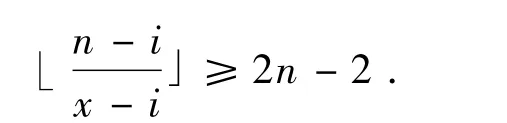
解此不等式可得:i=0,x=1.即
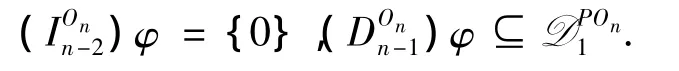
类似[8]中的方法可证,此时φ具有形式(5).
当1≤k≤n-3 时,IOnn-3为 Kerφ 的一个同余类,设(IOnn-3)φ =f,显然 f∈E(POn).为讨论此情况.首先引入以下引理:
引理1 令 g,h∈DOni,其中,k+1≤i≤n-2.则 g R h当且仅当(g)φR(h)φ;g L h当且仅当(g)φL(h)φ.
证明 在此只证明R关系,类似可证L关系.
若g R h,因为φ是同态,所以有(g)φR(h)φ.
反之,令(g)φR(h)φ.因为IOni是On的正则子半群,故有(IOni)φ是POn的正则子半群.由[9],令
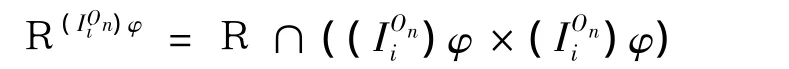
则有
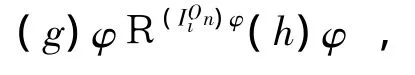
故存在 a,b∈IOni,使得
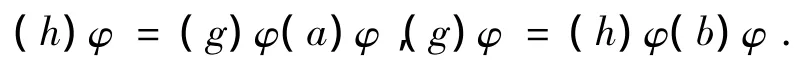
若 r(ga)≤k,则有(ga)φ =f:

故h∈(f)φ-1=Ik,矛盾.因此r(ga)>k.同理可得r(hb)>k.又因为φ在On/IOnk上的单射,故有:
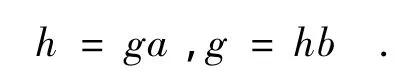
即g R h.
引理2(DOnk+1)φDPOnl,其中,r(f)<l<k+1.
该引理的证明类似[1]中的证明方法,此时不再重复证明.
今
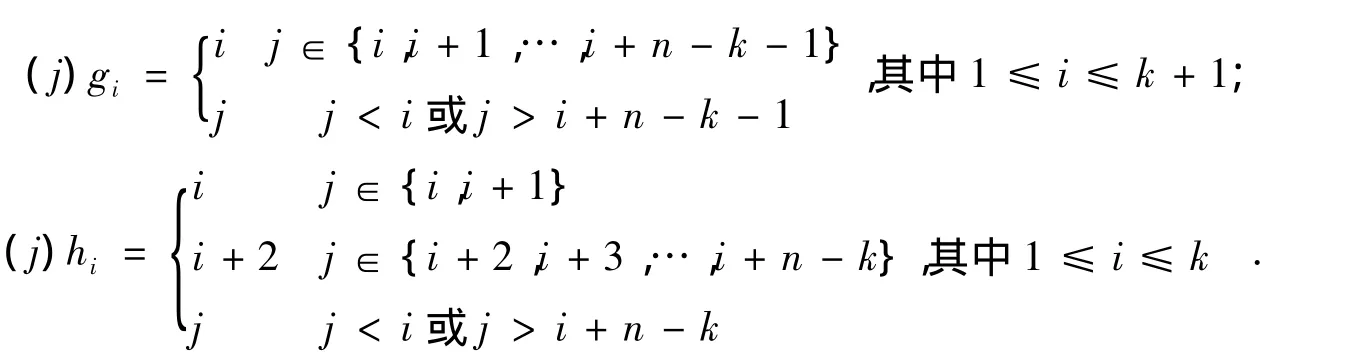
令G={g1,…,gk+1,h1,…,hk}.则G中的元素均为的幂等元,且任意两个的复合都在中.若k=n-3,则对任意的 1≤i≤k,有 gi=hi,此时=n-2.若 k<n-3,则由由引理1知,中共有类.引理2知,其中l<k+1中共有个类,故,因此有今 ε1,ε2,…,εn-2∈G.对任意 u∈On,有 f·(u)φ =f,因此有
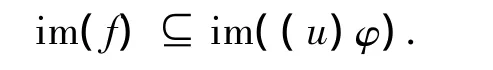
特别的,有
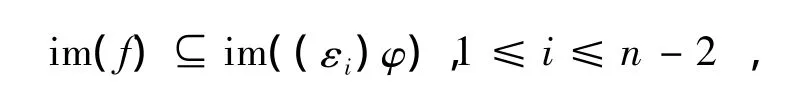
显然,若 i≠j,有
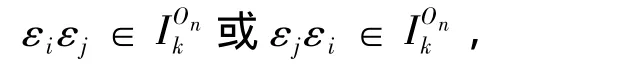
故有

因为(εi)φ,(εj)φ 为幂等元,故有
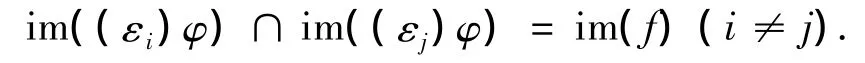
今 E′i=im((εi)φ)/im(f),1≤i≤n-2,则 E′1,E′2,…,E′n-2两两互不相交.(ε1)φ,(ε2)φ,…,(εn-2)φ∈(DOnk+1)φ.由引理2知,
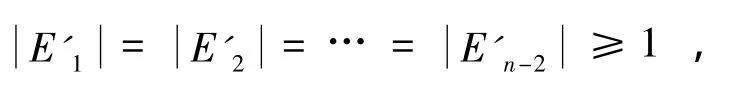
故有
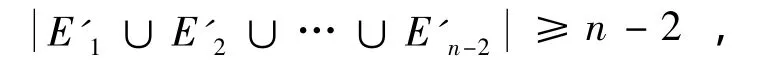
由此可得
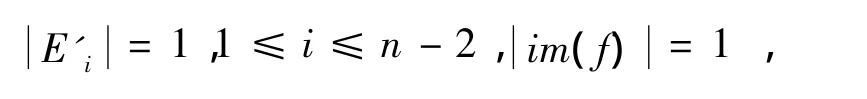
即
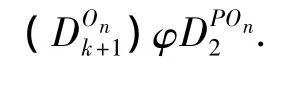
且对任意 u∈DOnk+1,有
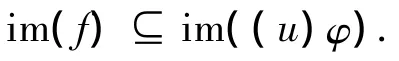
因此(DOnk+1)φ至多包含n-2个不同的L类.由引理1知,DOnk+1至多有n-2个不同的L类.故k+1=n,矛盾.即证.
4 定理2的证明
设α∈POn,且α为秩为i的幂等元.由[5]知,On中秩为r幂等元由(n+r-12r-1)个,由此可计算出当时,此时的α共有(n+i-12i-1)个;
…
相加可得,在POn中,秩为i的幂等元个数为
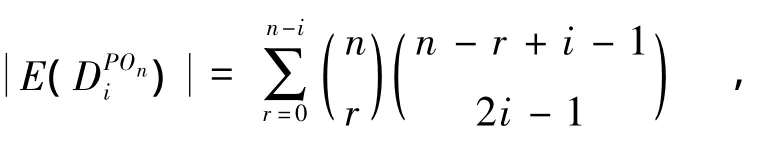

设 e∈E(POn),并今 S(e)={f∈E(POn)∶ef=fe=f},则 On到 POn具有形式(3),(4)的同态的个数分别为和1,其中(ln)φ =e.
又由[4]知
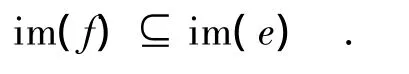
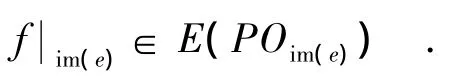
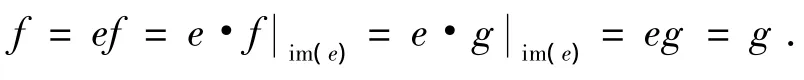
故ψ是单射,所以有:
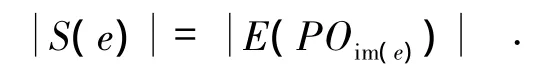
则由(1)式知
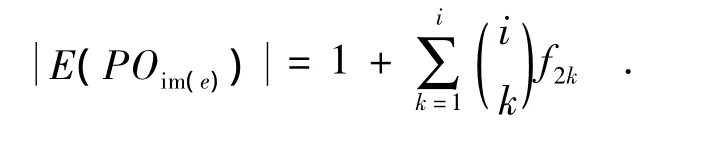
因此有
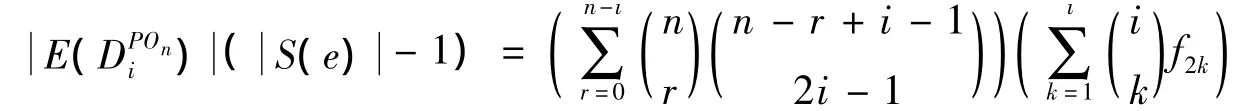
个具有形式(3)的同态,其中(1n)φ∈DPOni.
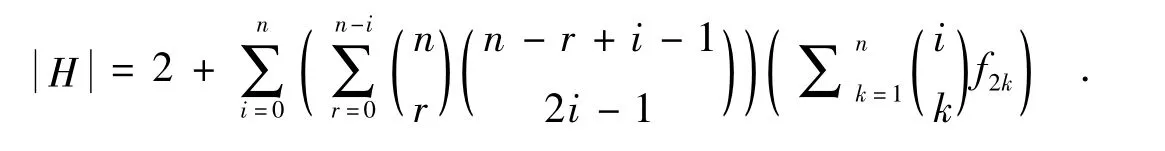
定理2得证.
[1]FERNANDESV H,JESUSM M,MALTCEV V,et al.Endomorphisms of semigroups of order-preserving mappings[J].Semigroup Forum,2010,81:277-285.
[2]LAVERST,SOLOMON A.The endomorphisms of a finite chain form a Rees congruence semi-group[J].Semigroup Forum,1999,59:167-170.
[3]杨浩波.保序部分变换半群上的同余[J].杭州师范大学学报:自然科学版,2007,6(3):13.
[4]GANYUSHKIN O,MAZORCHUK V.Introduction to classical finite transformation semi-group[M].London:Springer Ver-lag,2009.
[5]LARADJI A,UMAR A.Combinatorial results for semigroups of order-preserving partial transformation[J].Technical report series,2004,278(1):342-359.
[6]FERNANDESV H.The monoid of all injective order preserving partial transformations on a finite chain[J].Semigroup Forum,2001,62(2):178-204.
[7]AIZENSTAT J A.Homomorphisms of semigroups of endomorphisms of ordered sets[J].Uch Zap Leningr.Gos.Pedagog.Inst,1962,238:38-48.
[8]SCHEIN B.Teclezghi.B.Endomorphisms of symmetric semigroups of functions on a finite set[J].Comm Algebra,1998,19(26):3921-3938.
[9]HOWIE JM.Fundamentals of semigroup theory[M].New York:Oxford University Press,1995.
[10]HOWIE JM.An introduction to semigroup theory[M].New York:Academic Press,1976.
