基于STM32F10x的FIR滤波器设计与实现

,,,,

(1.上海师范大学 信息与机电工程学院,上海 200234; 2.上海计算机软件技术开发中心,上海 201114)

0 引 言

STM32F10x系列是ST公司针对工业、医疗和消费类市场推出的基于ARM cortex-M3内核的微控制器,该系列包含五大产品线:STM32F100具有电机控制和CEC功能;STM32F101具有高达1MB的Flash;STM32F102具有USB全速设备功能;STM32F103具有高达1MB的Flash、电机控制、USB和CAN接口;STM32F105/107具有以太网MAC、CAN和USB2.0 OTG.

无论针对工业控制、医疗服务或者消费类领域,传感器已经成为电子设备中不可缺少的部分,如:工业称重设备使用的压阻式压力传感器、医疗仪器中常见的心率脉搏传感器、智能手机中的重力传感器等.传感器将各种模拟信号转换成电压信号后,需要通过模数转换器(A/D)将电压信号转换成数字信号,然后再输出到处理器进行相应信号处理,传感器的信号处理框图如图1所示.

图1 通过传感器的模拟信号处理框图

然而,模拟信号极易受到外界干扰,如传感器未能水平放置,风向、风力大小的影响,日光灯的工频干扰,甚至是微小的震动,都会对传感器获得的信号造成扰动,去除这些干扰最有效、最经济的方法就是处理器对输入的数字信号进行信号滤波的去噪预处理.根据滤波器单位脉冲响应的时间特性,滤波器可分为FIR滤波器和IIR滤波器两类,由于FIR滤波器只包含有限个系数、无输入反馈,以及结构简单等特点,使FIR滤波器成为实际应用系统中最常用的滤波器类型.

DSP(数字信号处理器)和FPGA(可编程逻辑门阵列)是实现数字滤波器最常用的处理器,其中DSP适合实现串行的滤波器结构,FPGA适合实现并行的滤波器结构.虽然这两种处理器具有超强的处理能力,但是价格昂贵,作为传感器信号的滤波器实现可谓大材小用.滤波运算需要大量的乘法,常用的单片机由于没有硬件乘法器,实现滤波器需要占用大量的CPU时钟,这势必影响系统中其他处理的正常工作.STM32F10x系列微控制器采用RISC结构,并内嵌硬件乘法器以及大量片内外设,同时兼顾了低成本优势,特别适合于传感器信号的FIR滤波器实现和数字信号处理.

1 FIR滤波器的原理、设计方法及基本结构

对长为N的数字滤波器的单位脉冲响应,其传输函数为:

(1)

其中ω为数字频率,Hg(ω)为幅度特性函数,θ(ω)为相位特性函数.

为保证信号的群延时为常数,要求所设计的FIR滤波器是线性相位,即相位特性函数θ(ω)满足:

θ(ω)=-τω,

(2)

θ(ω)=θ0-τω.

(3)

其中τ为常数,θ0为起始相位,-π≤ω≤π.公式(2)表示第一线性相位,公式(3)为第二线性相位.

为设计线性相位FIR滤波器,经过推导[1]可得,线性相位FIR滤波器的单位脉冲响应,应满足:

h(n)=h(N-1-n), 0≤n≤N-1 ;

(4)

h(n)=-h(N-1-n), 0≤n≤N-1 .

(5)

其中,h(n)满足公式(4),则所设计的FIR滤波器是第一线性相位;h(n)满足公式(5),则所设计的FIR滤波器是第二线性相位.

FIR滤波器设计常用的3种方法是窗函数设计法[1]、频率取样法和优化设计法,其中使用最广泛是窗函数设计法,常用的窗函数[1]有矩形窗、海明窗、汉宁窗、莱克曼窗和凯塞-贝塞尔窗,其中从频域特性看,莱克曼窗与前几个窗函数相比,主瓣宽度窄、旁瓣衰减快;与凯塞-贝塞尔窗相比,虽然凯塞-贝塞尔窗是一种可调节的窗函数,但是在提高频域特性的同时,其时域的幅值较难整型化,同时也会使得过渡带变宽,综合工业控制领域对滤波的需求,采用布莱克曼窗(blackman),通过matlab软件设计得到滤波器的单位脉冲响应h(n).

FIR滤波器的基本结构主要有:直接型FIR、级联型FIR、线性相位型FIR、频率取样型FIR等结构,其中直接型FIR滤波器结构为串行运算结构[2],较符合微控制器按照程序顺序执行的特点.直接型FIR滤波器结构[3]如图2所示,其结构就是描述了信号xn经过系统的卷积运算.

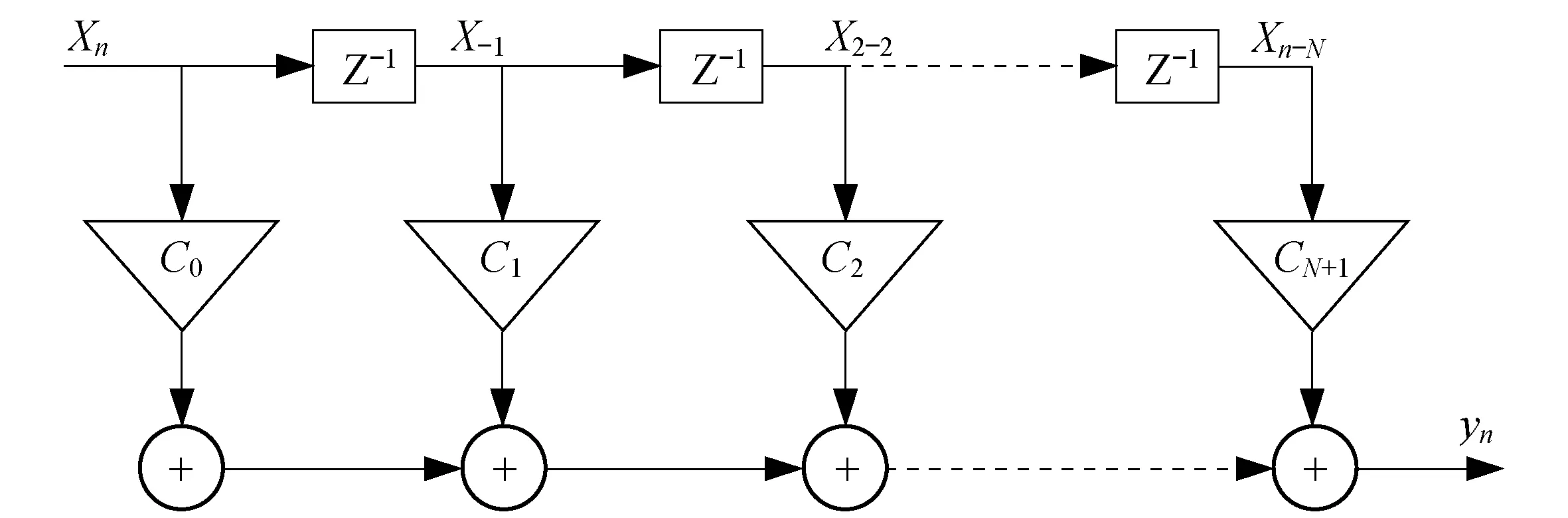
图2 直接型FIR滤波器结构

图2中,xn…xn-N表示输入信号,yn表示第n时刻的输出信号,z-1表示延时1个单位时间,c0,…,cN-1表示相应输入信号乘以相应的系数.

2 基于STM32F10x数字信号处理器库的FIR滤波器实现原理

ST公司在推出STM32F10x系列MCU的同时,推出了STM32F10x数字信号处理库,其中FIR滤波器的实现函数如表1所示.

表1 STM32F10x DSP library中FIR滤波器函数原型

其中COFFS结构体的定义如下:

其中,h为滤波器系数,nh为滤波器阶次.

这里需要注意,fir_16by16_stm32函数并不能实现滤波器设计,函数只是将信号x与系数p以图2方式(直接型FIR滤波器结构)运算后得到一个运算结果,实际是完成了信号x与系数p的线性卷积运算[1],如公式(6)所示:

(6)

其中,x、h为2个信号,x={x0,x1,...,xL-1},h={h0,h1,...,hM-1},卷积结果y的长度为M+L-1.

通过分析fir_16by16_stm32函数,调用函数得到的运算结果如公式(7)所示:

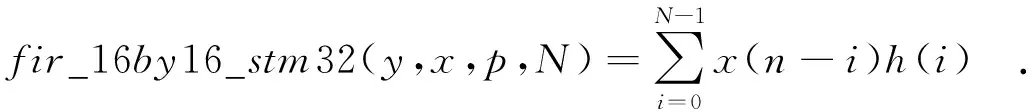
(7)

其中,N即为函数原形中的第4个参数(表1).

因此,为尽可能节约STM32F10x芯片内的内存资源,同时减少运算耗时,在编程过程的数据定义时,应满足公式(8):

N=L-M.

(8)

即滤波结果的数组长度等于信号数组长度与滤波系数数组个数的差.

另外值得注意的是,STM32F10x系列微控制器只支持整数运算,浮点数的运算通过编译将转化为整数运算,但运算效率大大降低.同时为了使用fir_16by16_stm32函数,通过表1,可以看到信号数组x及滤波器数组h的数据类型为short型,即数值范围在-215～+215-1,因此,信号xi应满足:

-215≤xi≤215-1 .

(9)

通过matlab软件设计后的滤波器系数以归一化的数值方式得到,即:

(10)

因此,在使用fir_16by16_stm32函数时并不能直接使用matlab软件设计的滤波器系数,而必须经过数值变换,如图3所示.数值放大过程中,考虑到最后需要恢复原数值范围,建议放大倍数为2n,n为整数,这可以使后期数据恢复时,只需要进行移位操作,相比于除法运算,运算量大大降低.无论使用数值扩大以后采用四舍五入、向上取整或者向下取整,最后去除小数的同时依然会导致一些误差,因此最后需要对整型化的系数作微调.

图3 滤波器系数的数值变化框图

从表1可以看到,滤波结果数组的数据类型为int型,即32位有符号整型,所以应保证滤波结果的每个数值的绝对值应小于231,因此按照公式11,可推导出数值放大倍数(A)的限制:

(11)

其中,N为滤波器阶次,max(xi)表示信号各系数的最大值.当然,在对系数进行放大的同时,应该考虑应用的精度需求.

3 实验结果与分析

3.1 滤波器设计

采用matlab软件为设计工具,滤波器设计采用窗函数法,采用布莱克曼窗,滤波器点数取64点.设信号采样率为256样值/s,滤波器截至频率为10Hz,滤波器时频域特性如图4所示:

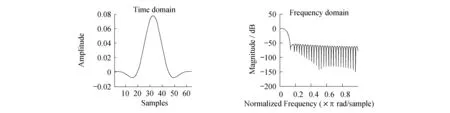
图4 截至频率为10Hz的FIR滤波器时频特性

3.2 滤波器数值变换

表2 滤波器放大倍数实验结果

为使用STM32F10x数字信号处理库,利用matlab设计的滤波器的系数需要进行变换,为保证每个系数的可见性,即通过数值变换后最小系数至少为0或1,按照滤波器阶次,通过实验得到各阶次滤波器的放大倍数,如表2所示.

表2的实验结果只是考虑了系数整数化以后的可见性,同时考虑公式(11)时,可以看到当滤波器点数为64点或128点时,如果信号的数值过大就会造成运算结果溢出,即超出表1中滤波器输出数组的数据类型.

3.3 基于STM32F10x的滤波结果分析

实验所用平台采用STM32F107为主处理器的评估板,板上配有LCD显示屏、网口、wifi模块、zigbee模块、传感器等模块,完全能够满足测试需求.

假设采样率为256样点/s,以5 Hz和50 Hz组成原始信号,如图6所示.

图6 被测信号时域及频域特性

设计10 Hz的滤波器,并整型化后的结果如图7所示.

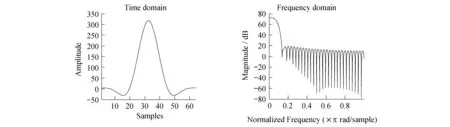
图7 整型化后的10Hz FIR滤波器

对图6所示原始信号进行滤波后的结果如图8所示.

图8 原始信号经过滤波器后的结果

图6的原始信号经过如图7的滤波器后,50 Hz的噪音信号已经被完全滤除,图8中的时域信号已经可以被认为是5Hz的单频信号,达到预期的FIR滤波器的效果.

3.4 基于STM32F10x的滤波器性能分析

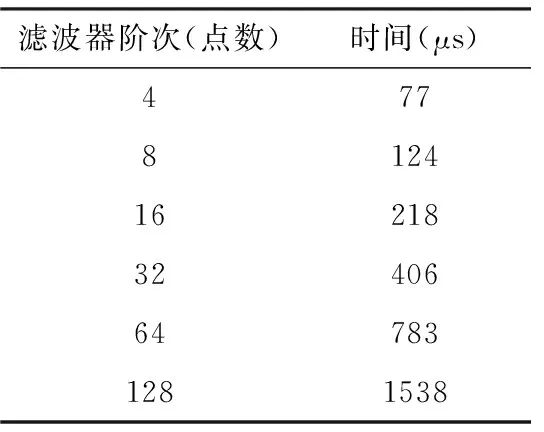
表3 滤波器性能测试结果

本节主要分析基于STM32F10x的时间特性,测试平台依然采用STM32F107VC为主处理器,并且工作频率设置在72 MHz.假设信号采样率为256样点/s,以表2所示阶次滤波器为测试对象,以测试各阶滤波器滤波1 s采样信号(即256点信号)所耗时间,如表3所示.

从表3实验结果看,256阶滤波器对128点信号的滤波时间仅为1.5 ms,滤波效率完全能够满足通常滤波器的需求.这里需要注意的是,64阶和128阶测试过程中,为了使滤波结果真实有效(即数据在运算过程中不发生越界),信号值控制在210以内,因此完全够满足常用的8位或10位,即STM32F10x平台的片内A/D能够使用128阶滤波器.

4 结 论

基于STM32F10x平台,作者提出了FIR滤波器的设计与实现方法,包括滤波器在matlab平台下的设计,及在STM32F10x平台利用STM32F10x DSP Lib进行滤波器实现的整套方案,通过测试表明,滤波器的滤波结果与仿真要求一致,在72 MHz主频下,以256/s采样率,采用128阶FIR滤波器对1 s数据的滤波器的时间仅为1.5 ms,完全满足通常的滤波时间需求.

参考文献:

[1] 李莉.数字信号处理原理和算法实现[M].北京:清华大学出版社,2010.

[2] 章晓眉,赵冬娥,冯彦君,等.基于FPGA的FIR滤波器设计[J].电子质量,2011(9):29-41.

[3] 戴曜泽,王春雷,朱智强.基于FPGA高阶FIR滤波器的实现[J].现代电子技术,2012,35(8):111-113.